#5 Yearn Finance事件：不安全的算术运算导致收益求解器名副其实

2025年11月30日，Yearn Finance 的 yETH 加权稳定池被利用，损失超过 900 万美元 [1]。根本原因在于 _calc_supply() 恒定求解器中的不安全算术 以及 未禁用的引导路径，这允许重新进入初始化逻辑。官方事后分析 [2] 列出了五个根本原因；我们将其重新归类为两个缺陷（上述漏洞）和两个架构先决条件，这些先决条件只有在存在这些缺陷时才可被利用。其他可用分析侧重于分步攻击交易细节。在高层摘要和交易级细节之间，仍然存在一个差距：攻击是如何以及为何真正起作用的？本文通过使用 Foundry 和 Python 模拟来填充这个差距，追踪关键值的逐步演变以及计算的失败之处。

本次分析主要做出以下三点贡献：

1. 按漏洞细分损失。 两个漏洞并不相互依赖：不安全算术本身就造成了约 810 万美元的损失（占总数的 90%），而引导路径则额外造成了约 90 万美元的损失。这阐明了哪个漏洞是主要的。
2. 重新归类根本原因。 官方报告中的五个根本原因被更好地理解为两个实现缺陷（整合了五个项目中的三个）加上两个架构先决条件，这些先决条件只有在与缺陷结合时才可被利用。
3. 纠正技术误解。 “第二次迭代中的下溢使乘积项归零”的说法不成立：我们的模拟显示乘积项通过除法中的舍入归零，而不是下溢，而产生利润的下溢发生在完全不同的阶段。

本文其余部分的组织结构如下。0x1 节介绍 yETH 加权稳定池及其恒定求解器的背景。0x2 节分析了两个根本原因及其故障模式。0x3 节详细追踪了三阶段攻击。0x4 节通过模拟证据纠正了两个常见误解。0x5 节总结并提出建议。

TL;DR

根本原因： 两个漏洞被利用，但影响不对称：

1. _calc_supply() 中的不安全算术（主要，约 810 万美元）。该函数从池状态重新计算 yETH 供应，包含两个算术故障：unsafe_div() 中的向下舍入可能导致内部乘积项归零，以及 unsafe_sub() 中的下溢可能将中间值包装成一个巨大的正整数。仅此漏洞就足以耗尽 yETH 加权稳定兑换池。
2. 未禁用的引导路径（次要，约 90 万美元）。prev_supply == 0 的初始化分支在部署后从未被永久禁用。在第一个漏洞将供应耗尽至零后，该路径变得可达，从而可以通过 yETH/WETH Curve 池实现额外利润。

在不安全算术漏洞中，只有向下舍入故障（故障模式 A）在第二阶段被使用（约 810 万美元）；下溢故障（故障模式 B）与引导路径相互依赖，两者共同启用了第三阶段。

攻击者执行了三阶段序列：

1. 准备： 通过重复的添加/移除循环来扭曲池的资产分配，造成虚拟余额的极端失衡。
2. 供应操纵： 利用 _calc_supply() 中的向下舍入将乘积项压缩为零，然后通过一系列的铸造/销毁操作将总供应量降至零。所有池的 LST 都被提取并兑换成 WETH，导致约 810 万美元的损失。
3. 利润提取： 通过粉尘存款触发引导路径 (prev_supply == 0)，利用 _calc_supply() 中的下溢铸造约 2.35×10⁵⁶ 个 yETH，这些 yETH 被用于耗尽 yETH/WETH Curve 池，导致约 90 万美元的损失。

纠正了两个常见误解：

• “恒定值因 pow_up() 和 pow_down() 舍入不同而失效。” 我们通过在 Foundry 模拟中将 pow_up() 替换为 pow_down() 来验证：漏洞依然存在。舍入不匹配不是根本原因。
• “第二次迭代中的下溢使中间项归零。” 我们的 Foundry 和 Python 模拟显示第二次迭代中没有发生下溢。实际值约为 1.91e19（而非声称的约 1.94e18），这是正确减法的一个合法结果。使乘积归零的是随后的除法中的向下舍入，而不是下溢。

0x1 背景

在此次事件中，两个池损失了资产：yETH 加权稳定兑换池（一个 Yearn 池，持有 LST，损失约 810 万美元）和yETH/WETH Curve 池（一个 Curve 稳定兑换池，损失约 90 万美元）。yETH 加权稳定兑换池是核心漏洞所在。本节提供了理解漏洞和利用所需的背景信息。

0x1.1 虚拟余额与恒定值

yETH 协议是用于以太坊流动性质押代币（LST）的自动化做市商（AMM）[3]。受影响的yETH 加权稳定兑换池将多个 LST 聚合到一个池中：用户存入 LST 并获得 yETH 作为池份额代币。

由于每个 LST 代表质押的 ETH 并随时间累积奖励，其相对于基础 ETH 的汇率会发生变化。为了统一核算，池为每种资产定义了一个虚拟余额 $x_{i}x\_i$：链上余额 × 汇率。这将所有资产标准化为信标链 ETH 单位。所有虚拟余额的总和表示为 $\sigma =\sum x_i\backslash sigma\; =\; \backslash sum\; x\_i$。

池包含 8 种资产（索引 0-7），每种资产都有指定的权重 $w_{i}w\_i$：

池的状态由加权稳定兑换式恒定值 [4] 决定：

$$\begin{array}{cccc}& {Af}^n\sigma +D={Af}^{n}D+D\cdot \pi & & \text{(1)}\end{array}\backslash mathit\{Af\}^\{\backslash ,n\}\backslash ;\backslash sigma\; +\; D\; =\; \backslash mathit\{Af\}^\{\backslash ,n\}\backslash ;D\; +\; D\; \backslash cdot\; \backslash pi\; \backslash tag\{1\}$$

其中：

• $DD$ 是恒定规模，直接等于此池的总 yETH 供应量。当池完美平衡时，$D=\sigma D\; =\; \backslash sigma$。
• $\pi \backslash pi$ 是加权乘积项，定义为 $\pi =D^n{\prod }_i{\left(\frac{w_i}{x_i}\right)}^{v_i}\backslash pi\; =\; D^n\; \backslash prod\_\{i\}\; \backslash left(\backslash frac\{w\_i\}\{x\_i\}\backslash right)^\{v\_i\}$，其中 $w_{i}w\_i$ 是资产 i 的权重，而 $v_i=w_i\cdot nv\_i\; =\; w\_i\; \backslash cdot\; n$。
• $Af\backslash mathit\{Af\}$ 是放大因子，一个单一的协议参数（非 $A\times fA\; \backslash times\; f$）。${Af}^n\backslash mathit\{Af\}^\{\backslash ,n\}$ 表示此因子升高到 $nn$ 次幂，其中 $nn$ 是资产数量（此池中为 8）。它控制着恒定求和（接近平衡）和恒定乘积（极端情况）之间的曲线形状。

关键属性：$DD$ 没有封闭形式解。它必须通过数值求解。该求解器 _calc_supply() 是算术漏洞所在的代码。

0x1.2 恒定求解器

协议通过一个上限为 256 轮的定点迭代来重新计算 $DD$。该算法在代码中实现为 _calc_supply()（详见 0x2.1 节）。每轮执行三个步骤：

步骤 1：更新供应估计。

$$\begin{array}{cccc}& D_{m+1}=\frac{{Af}^n\cdot \sigma -D_m\cdot {\pi }_m}{{Af}^n-1}& & \text{(2)}\end{array}D\_\{m+1\}\; =\; \backslash frac\{\backslash mathit\{Af\}^\{\backslash ,n\}\; \backslash cdot\; \backslash sigma\; -\; D\_m\; \backslash cdot\; \backslash pi\_m\}\{\backslash mathit\{Af\}^\{\backslash ,n\}\; -\; 1\}\; \backslash tag\{2\}$$

步骤 2：更新乘积项以匹配新的供应。

$$\begin{array}{cccc}& {\pi }_{m+1}={\pi }_m\cdot {\left(\frac{D_{m+1}}{D_m}\right)}^n& & \text{(3)}\end{array}\backslash pi\_\{m+1\}\; =\; \backslash pi\_m\; \backslash cdot\; \backslash left(\backslash frac\{D\_\{m+1\}\}\{D\_m\}\backslash right)^n\; \backslash tag\{3\}$$

步骤 3：检查收敛性。

如果 ，则返回 $D_{m}D\_\{m\}$；否则从步骤 1 开始重复。

初始值 $D_{0}D\_0$、${\pi }_0\backslash pi\_0$ 和 $\sigma \backslash sigma$ 会影响早期迭代；尽管理论上对最终收敛无关紧要，但由于有限迭代和固定精度算术，它们在实践中会影响结果。

实现使用固定精度整数运算：除法向下舍入，减法不防范下溢。在正常池条件下，中间值保持在安全范围内。在极端池状态下，它们不会。0x2.1 节详细分析了这些故障模式。

0x1.3 三个接口与恒定求解器

协议暴露三个影响池状态的入口点，通过更新加权乘积项 $\pi \backslash pi$（代码中存储为 vb_prod）：

不对称性很重要：add_liquidity() 允许任意比例存款（可以极大地扭曲池），而 remove_liquidity() 总是按比例提取。因此，重复的添加/移除循环可以将池推入越来越不平衡的状态。

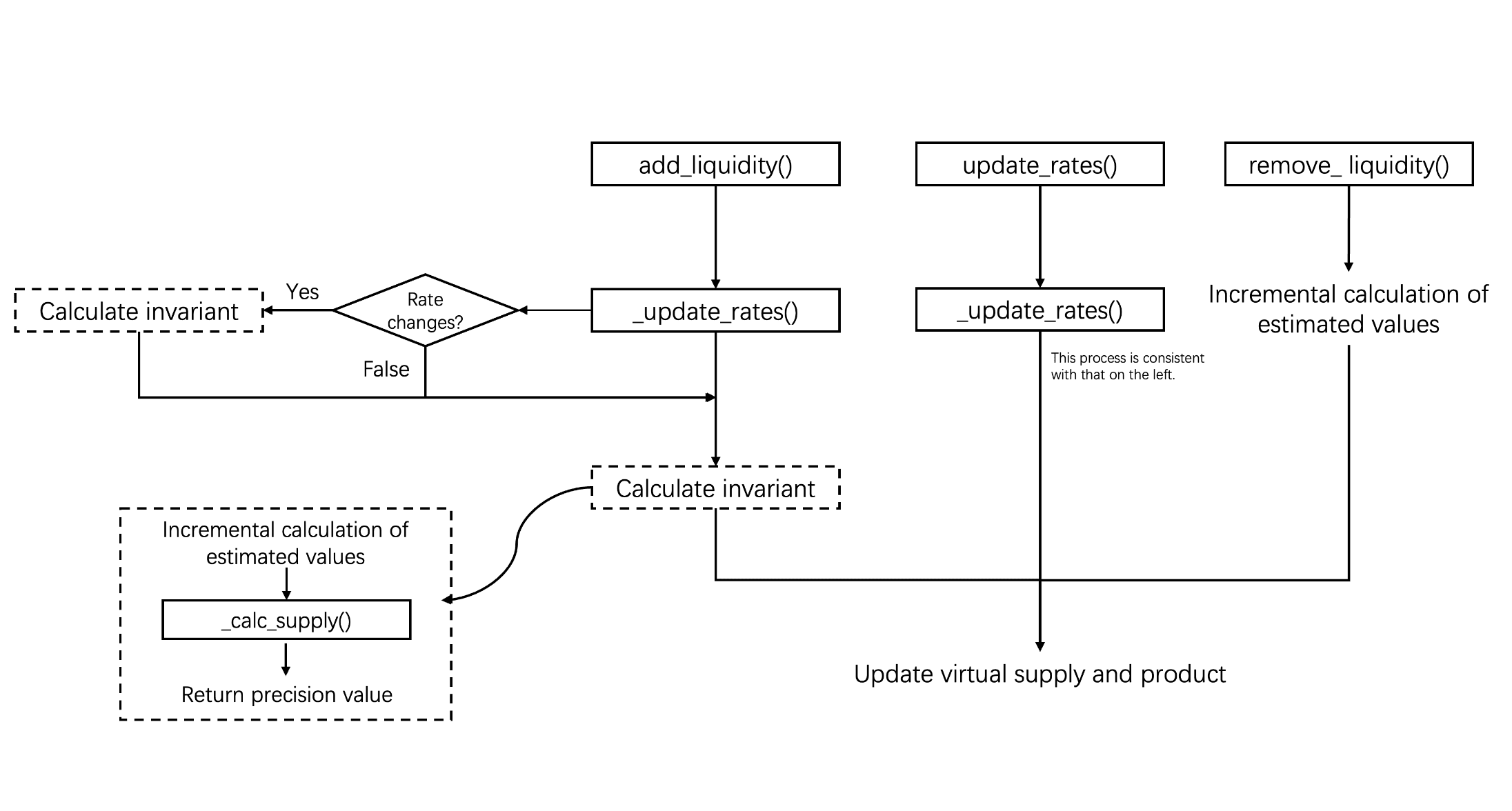
更新汇率的机制

如上所述，虚拟余额 ($x_{i}x\_i$) 是基于 LST 的汇率计算的。因此，理解更新汇率的方式很重要。

具体来说，add_liquidity() 和 update_rates() 函数可以通过内部函数 _update_rates() 更新汇率，而 remove_liquidity() 函数不执行汇率同步。

• add_liquidity() 在执行关键操作之前调用 _update_rates()，以确保资产汇率与最新状态同步。
• update_rates() 允许手动更新汇率。

_update_rates() 函数检查合约中记录的汇率是否与外部汇率一致。如果检测到差异，它将触发对虚拟余额的重新计算，并随后更新恒定值；否则，将跳过更新过程。

每个接口如何处理 π

基于它们如何影响恒定值，这三个函数可以分为两类。具体来说，add_liquidity() 和 update_rates() 允许虚拟余额发生非比例变化，因此需要迭代重新计算供应 $DD$ 和乘积 $\pi \backslash pi$。相反，remove_liquidity() 按比例提取流动性，不需要迭代计算。

从头开始计算乘积的基础公式为：

$$\begin{array}{cccc}& \pi =\prod _i{\left(\frac{D\cdot w_i}{x_i}\right)}^{n\cdot w_i}& & \text{(4)}\end{array}\backslash pi\; =\; \backslash prod\_\{i\}\; \backslash left(\backslash frac\{D\; \backslash cdot\; w\_i\}\{x\_i\}\backslash right)^\{n\; \backslash cdot\; w\_i\}\; \backslash tag\{4\}$$

其中 $DD$ 是供应量，$w_{i}w\_i$ 是资产 $ii$ 的权重，$x_{i}x\_i$ 是其虚拟余额（代码中存储为 vb[i]），$nn$ 是资产数量。此形式在代数上等同于 0x1.1 节中的定义，其中 $D^{n}D^n$ 被分配到乘积中。

1. add_liquidity() 有两个路径（代码见 0x2.2 节）：

   • 引导路径（当 prev_supply == 0 时）：从头开始使用公式（4）计算 vb_prod。该路径在部署后仍然可访问是 0x2.2 节讨论的状态管理漏洞。
   • 正常路径（当 prev_supply > 0 时）：计算过程分为两步：
     • a) 使用基于旧虚拟余额与新虚拟余额之比的增量更新：

       $$\begin{array}{cccc}& {\pi }_{\text{estimated}}=\pi \cdot \prod _{i=0}^{n-1}{\left(\frac{x_i}{x_i^{\mathrm{\prime }}}\right)}^{w_i\cdot n}& & \text{(5)}\end{array}\backslash pi\_\{\backslash text\{estimated\}\}\; =\; \backslash pi\; \backslash cdot\; \backslash prod\_\{i=0\}^\{n-1\}\; \backslash left(\backslash frac\{x\_i\}\{x\_i\text{'}\}\backslash right)^\{w\_i\; \backslash cdot\; n\}\; \backslash tag\{5\}$$

       其中 $x_{i}x\_i$ 和 $x_i^{\mathrm{\prime }}x\_i\text{'}$ 是存款之前的虚拟余额。
     • b) 通过调用 _calc_supply() 并以该估计值作为输入来迭代校准精确值，重新计算恒定值 $DD$ 和精确的 $\pi \backslash pi$ 值。

2. update_rates() 在汇率发生变化时触发，导致相应资产的虚拟余额被更新。其后续计算流程遵循 add_liquidity() 的正常路径，即迭代重新计算恒定值。此外，根据新计算的供应量，合约会铸造或销毁 yETH，以确保流动性供应与更新后的虚拟余额状态保持一致。

3. remove_liquidity() 在按比例减少每个虚拟余额后，始终使用公式（4）从头开始计算 vb_prod。

0x2 根本原因分析

两个漏洞被利用，具有不同的作用和影响。主要根本原因在于 _calc_supply() 恒定求解器中的计算缺陷，它有两种故障模式：(A) 向下舍入可能使乘积项归零，将恒定值退化为恒定求和模型并导致过量 LP 铸造（供应膨胀）；(B) 下溢条件也可能导致供应膨胀。仅故障模式 A 在第二阶段（约 810 万美元）被使用。故障模式 B 与次要漏洞相互依赖。

次要根本原因是一个状态管理缺陷：池的初始化分支仍然可达。在第二阶段将供应耗尽至零后，故障模式 B 与引导路径相结合，导致了额外的约 90 万美元损失（第三阶段）。

0x2.1 `_calc_supply()` 中的不安全算术（主要）

图 2 将 _calc_supply() 的实现映射到 0x1.2 节的数学过程，并标注了下面分析的两个算术故障点：

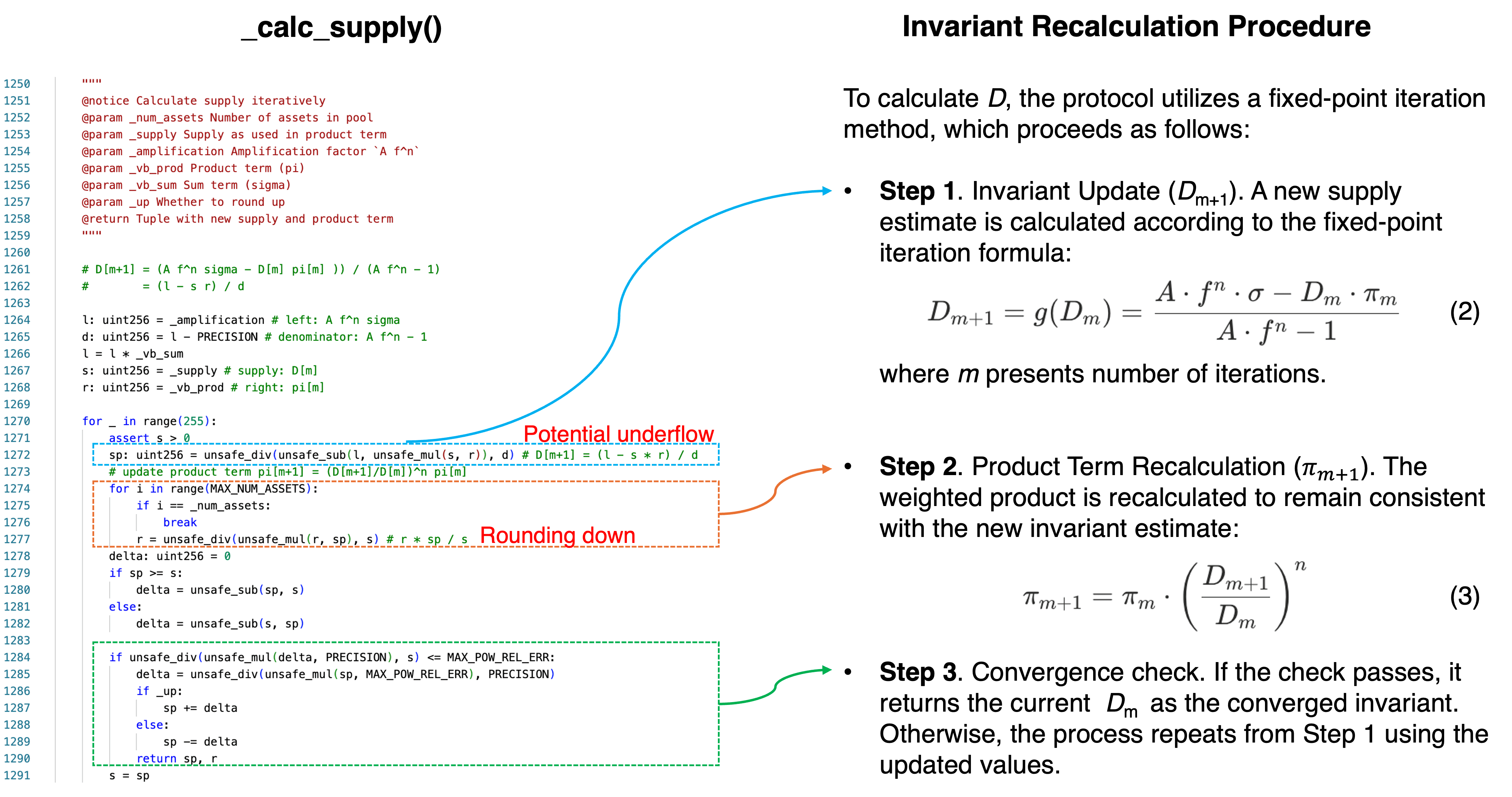
代码变量映射到数学项如下：

关键表达式为：

sp = unsafe_div(unsafe_sub(l, unsafe_mul(s, r)), d)   # 步骤 1: D[m+1]
r  = unsafe_div(unsafe_mul(r, sp), s)                 # 步骤 2: π 更新（每资产）

存在两种算术故障模式，针对不同的行并产生不同的效果。两者都需要池处于极端状态才能触发。

在正常条件下，迭代行为正确：l - s * r 是一个适度的正值，迭代在几轮内收敛。

1. 故障模式 A：向下舍入使乘积归零

在步骤 2 中，乘积按资产更新为：

r = unsafe_div(unsafe_mul(r, sp), s)   # r = r * sp / s

由于 unsafe_div() 执行整数除法，它始终向下舍入。当池严重失衡且 sp 远小于 s（在大量操纵性存款后发生）时，分子 r * sp 可能小于分母 s。整数除法随后产生**r = 0**。

一旦 r 为零，它在所有后续迭代中都保持零。乘积项 $\pi \backslash pi$ 已永久崩溃。

一个常见的归因错误声称此故障源于 pow_up() 和 pow_down() 之间的舍入不匹配。0x4 节提供了证据表明这是不正确的。

2. 故障模式 B：下溢导致供应膨胀

在步骤 1 中，新的供应估计计算如下：

sp = unsafe_div(unsafe_sub(l, unsafe_mul(s, r)), d)   # sp = (l - s*r) / d

l - s*r ${Af}^n\cdot \sigma -D_m\cdot {\pi }_m\backslash mathit\{Af\}^\{\backslash ,n\}\; \backslash cdot\; \backslash sigma\; -\; D\_m\; \backslash cdot\; \backslash pi\_m$ 在公式 2 中的减法。在正常条件下，这是正的。然而，当池达到零供应的退化状态时，add_liquidity() 中的初始化分支（详见 0x2.2 节）会从头开始重新计算乘积项，并且数量级可能会反转。

具体来说，当对零供应池进行“粉尘”金额的 add_liquidity() 调用时，初始化分支通过 _calc_vb_prod_sum() 计算新的值，使用公式（4）（0x1.3 节）。由于存款量很小，vb_sum 非常小（例如，16），但除以接近零的余额并提高到高次幂会放大乘积，使其达到不成比例的大值（例如，约 9.13e20）。当 s * r 超过 l 时，减法产生负的数学结果。

由于 unsafe_sub() 在未检查的 uint256 算术中执行减法，负结果会包装成一个巨大的正整数（接近 $2^{256}2^\{256\}$）。该包装值通过除法和后续迭代传播，产生一个荒谬的供应估计，然后协议将其作为真实 yETH 代币铸造。

一个常见的说法声称这种下溢发生在特定供应操纵步骤的第二次迭代中。0x4 节显示这种说法是不正确的：导致供应膨胀的实际下溢发生在完全不同的上下文中（攻击的第三阶段）。

3. 这些故障如何实现攻击

这两种故障模式在漏洞的不同阶段运行，具有不同的利润贡献：

• 故障模式 A（第二阶段，约 810 万美元）：当攻击者向严重失衡的池中存入资金时，乘积项归零，导致 _calc_supply() 返回膨胀的供应量。协议向攻击者超额铸造了 yETH。此故障模式本身，无需引导路径的任何参与，就使攻击者能够耗尽 yETH 加权稳定兑换池中的 LST 资产。

• 故障模式 B（第三阶段，约 90 万美元）：在供应量被耗尽至零后，引导路径通过粉尘存款重新计算了一个大的乘积项，导致减法下溢。协议铸造了天文数字的 yETH，攻击者利用这些 yETH 耗尽了单独的 yETH/WETH Curve 池，导致约 90 万美元的损失。

依赖关系是单向的：故障模式 A 可独立利用，造成了 90% 的损失；而故障模式 B 需要故障模式 A 首先将供应量降至零。

0x2.2 未禁用的引导路径（次要）

add_liquidity() 函数包含一个用于池初始存款的分支：

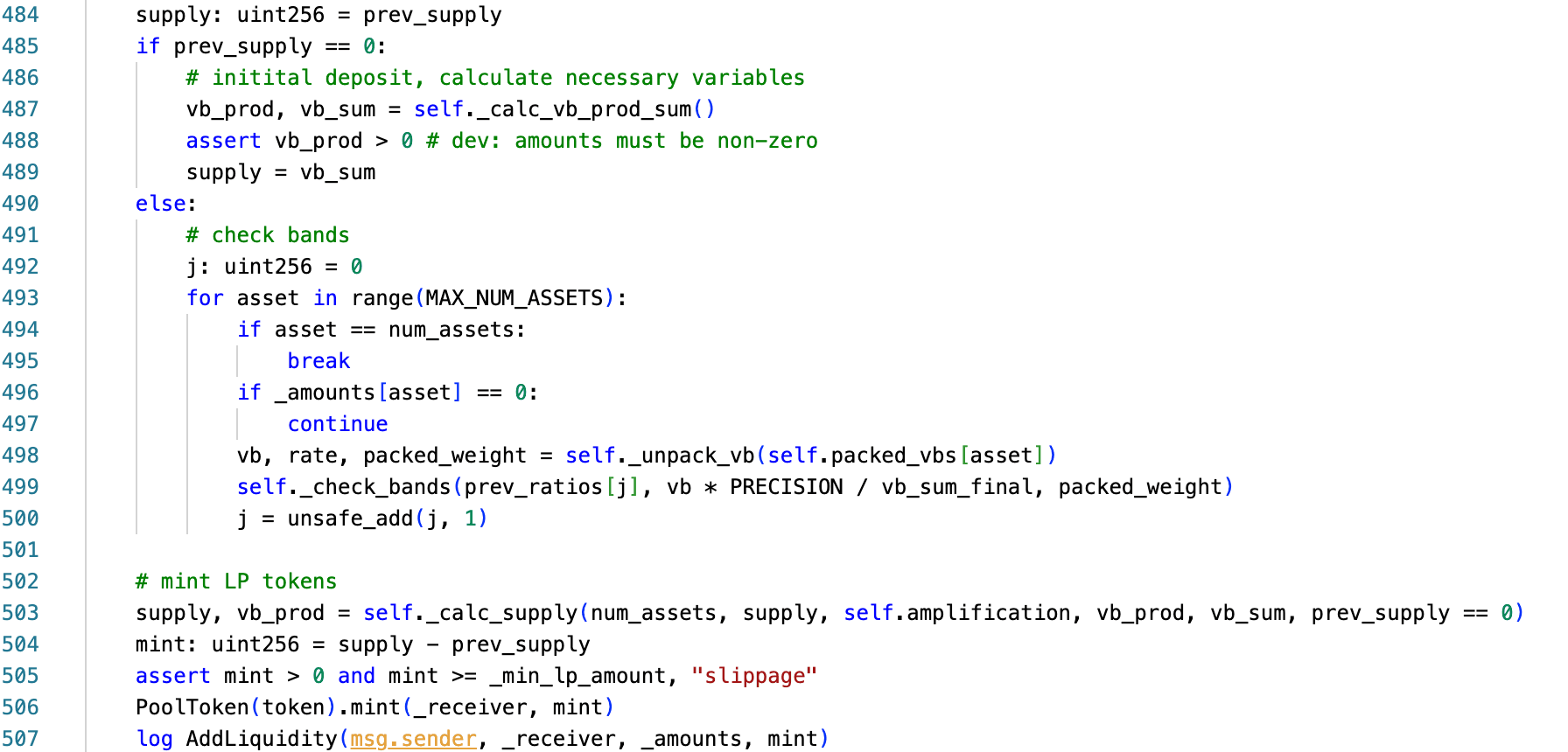
该逻辑可以抽象如下：

if prev_supply == 0:
    # 引导路径 — 从头计算 vb_prod 和 vb_sum
    vb_prod, vb_sum = _calc_vb_prod_sum(balances, rates, weights, ...)
    supply = vb_sum
else:
    # 正常路径 — 使用存储的 vb_prod，执行增量检查
    ...

# 在两个分支之后调用，prev_supply == 0 作为标志
supply, vb_prod = _calc_supply(num_assets, supply, amplification, vb_prod, vb_sum, prev_supply == 0)

当 prev_supply == 0 时，该函数会绕过存储的状态，并通过 _calc_vb_prod_sum() 从头开始重新计算 vb_prod 和 vb_sum，然后将这些值传递给 _calc_supply()。此引导分支原本设计用于池初始化期间的一次性使用，但在第一次存款后从未被永久禁用。

如果总供应量可以降至零（通过任何组合的销毁和提取），该分支将再次可达。利用此路径的攻击者可以控制传递给 _calc_supply() 的初始条件，可能在正常池操作永远不会出现的参数下触发上述算术故障。

这是一个已知的漏洞模式。2023 年 8 月，Balancer V2 事件也同样依赖于将供应量降至零以重置内部汇率，从而使攻击者能够以人为有利的参数重新进入初始化逻辑 [6]。部署的池是否可以恢复到其初始状态，以及在这种状态下哪些恒定值成立，这是协议设计者必须明确解决的问题。

0x3 攻击分析

此次利用通过一次协调的攻击交易 [5] 进行，分为三个阶段。每个阶段都建立在前一阶段建立的状态之上。

0x3.1 第一阶段：扭曲池（准备）

目标： 在资产之间造成极端的虚拟余额失衡。

下图说明了此阶段的交易追踪（出于空间限制，闪电贷步骤被省略）：

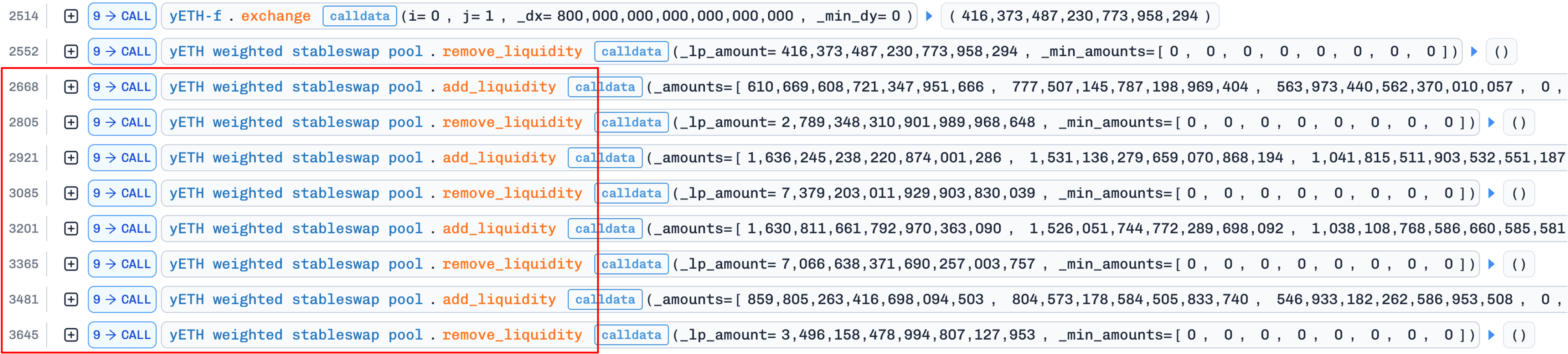
攻击者首先通过来自 Balancer 和 Aave 的闪电贷借入大量 LST 资产，特别是 5,500e18 wstETH、3,100e18 WETH、1,800e18 rETH、2,000e18 ETHx 和 200e18 cbETH。

接下来，攻击者在 yETH/WETH Curve 池中将约 800e18 WETH 兑换成约 416e18 yETH，然后使用获得的 yETH 从池中提取流动性。

核心操纵利用了 0x1 节（背景）中描述的接口不对称性：add_liquidity() 允许任意比例存款，而 remove_liquidity() 则按比例根据池权重提取资产（在上图的红色矩形中突出显示）。通过重复循环添加 → 移除操作，仅存入选定资产而按比例提取所有资产，攻击者逐步将池推入一个严重不平衡的状态：

资产 3 (cbETH)、6 (WOETH) 和 7 (mETH) 已被耗尽超过 98%。这种失衡不会直接提取利润。它为下一阶段创造了数值先决条件。

0x3.2 第二阶段：将供应量降至零（约 810 万美元）

目标： 将恒定值乘积降至零，然后将 yETH 供应量降至零。此阶段仅利用主要漏洞（不安全算术），造成了约 90% 的总损失。

此阶段使用重复的五步循环，执行三次：

1. 通过 add_liquidity() 破坏乘积；
2. 通过 add_liquidity() 建立纠正的先决条件；
3. 通过 remove_liquidity() 并设置 0 yETH 重置乘积；
4. 通过 update_rates() 纠正供应量；
5. 通过 remove_liquidity() 提取资产。

下图显示了此阶段的交易追踪，其中清楚可见五步循环的三次重复：

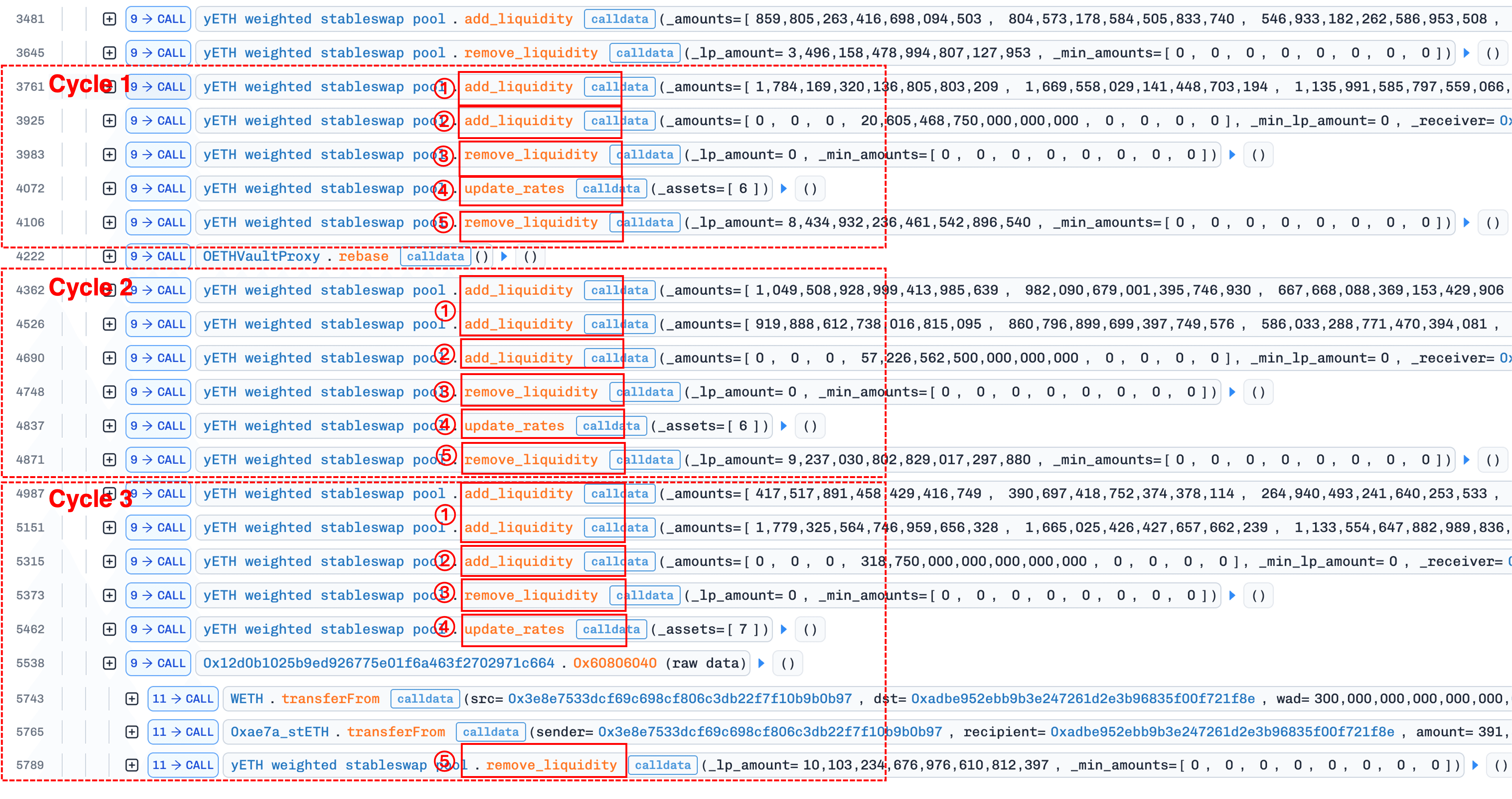
1. 通过 `add_liquidity()` 破坏乘积

攻击者存入大量高权重资产（索引 0、1、2、4、5：sfrxETH、wstETH、ETHx、rETH、apxETH），每种资产的存入量约为当前虚拟余额的三倍。

add_liquidity() 通过 0x1.3 节公式（5）中的增量更新来估计新的乘积项。由于高权重资产的 $x_i^{\mathrm{\prime }}\gg x_{i}x\_i\text{'}\; \backslash gg\; x\_i$，比率 $(x_i\mathrm{/}{x}_i^{\mathrm{\prime }})(x\_i\; /\; x\_i\text{'})$ 都是远小于 1 的分数，且被提升到高次幂。这导致 ${\pi }_{\text{new}}\backslash pi\_\{\backslash text\{new\}\}$ 从约 42e18 下降到约 0.00353e18，估计乘积接近于零。

该微小乘积进入 _calc_supply()。在迭代中，乘积更新 r = r * sp / s 遇到了 0x2 节（根本原因分析）中描述的向下舍入条件：分子小于分母，整数除法将 r 向下舍入为零。该函数返回一个零乘积和一个膨胀的供应量（约 vb_sum），导致协议超额铸造了 yETH。

2. 通过 `add_liquidity()` 建立纠正的先决条件

攻击者对资产索引 3（cbETH，一种已耗尽的低权重资产）进行单边流动性添加，存入约相当于该资产当前池余额的 6.5 倍。这只收到了很少的 yETH 代币，但足以重新平衡池，使得下一次迭代不会剧烈振荡。

如果没有这一步，即使在步骤 3 中将乘积重置为非零值，步骤 4 中的迭代仍会因极端失衡产生的剧烈振荡而产生零乘积。我们的 Foundry 模拟证实了这一点：跳过步骤 2 会导致步骤 4 中的纠正失败。

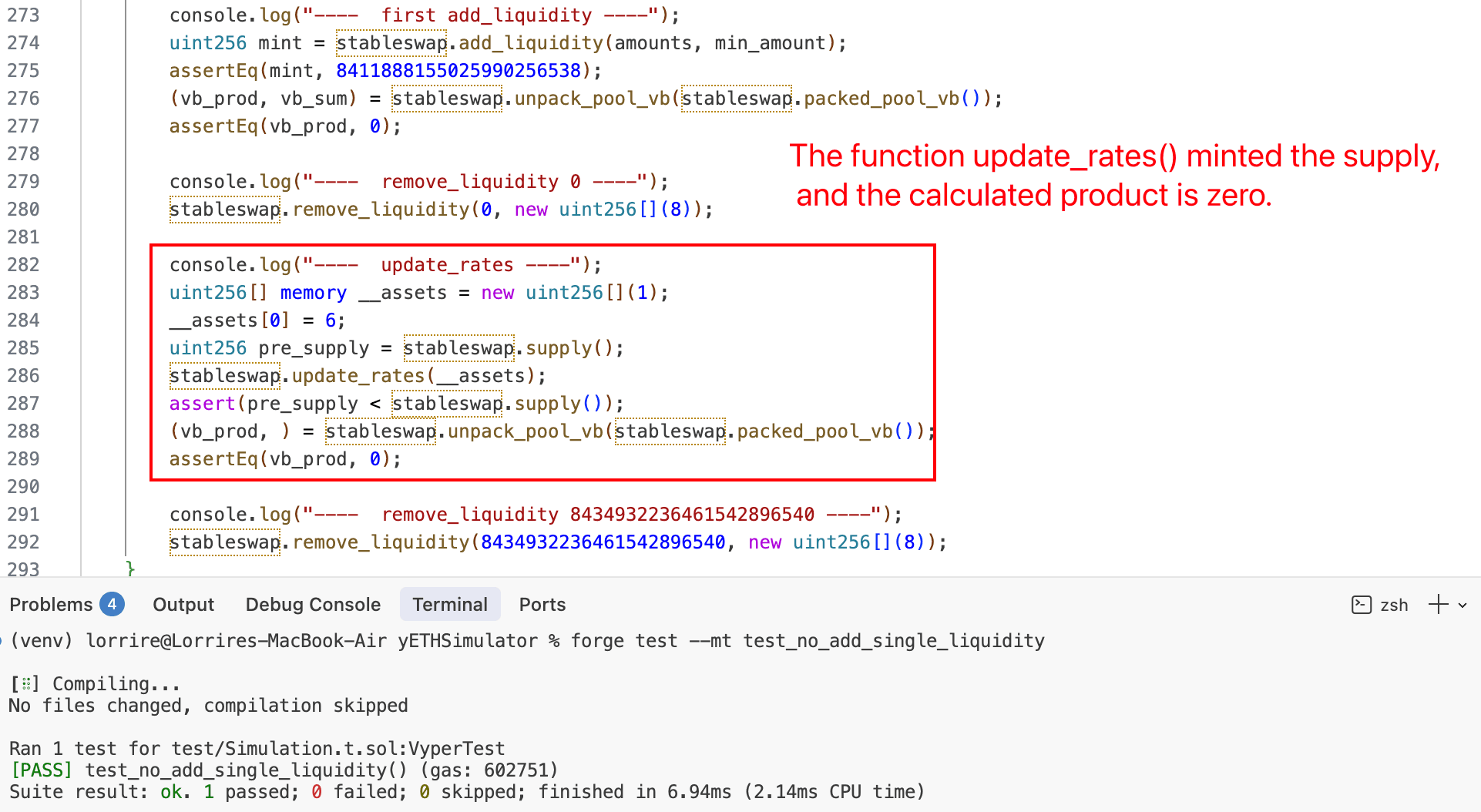
3. 通过 `remove_liquidity()` 并设置 0 yETH 重置乘积

攻击者在数量为 0 的情况下调用 remove_liquidity()。没有提取代币，但该函数使用当前池状态通过公式（4）（0x1.3 节）重新计算 vb_prod。由于虚拟余额不为零，这将产生一个非零乘积（约 9.09e19），覆盖了被破坏的零值。

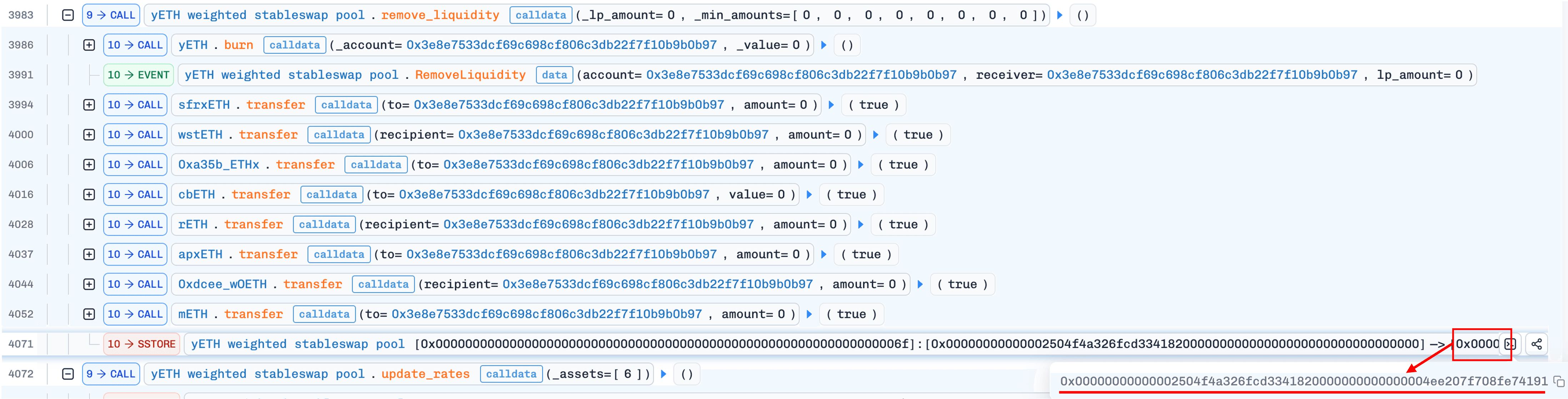
4. 通过 `update_rates()` 纠正供应量

攻击者为资产索引 6（WOETH）或 7（mETH）调用 update_rates()。如果自上次更新以来汇率发生变化，该函数将触发 _calc_supply()，并传入已恢复的（非零）乘积。这一次，迭代正确收敛，并产生一个远低于当前膨胀供应量的供应值。差额被销毁于 yETH 质押合约。根据官方事后分析 [2]，这构成协议拥有的流动性（POL），意味着销毁减少的是协议的头寸，而不是攻击者的持有量。这种不对称性至关重要：每次循环都会减少总供应量，而攻击者的 yETH 余额保持不变。

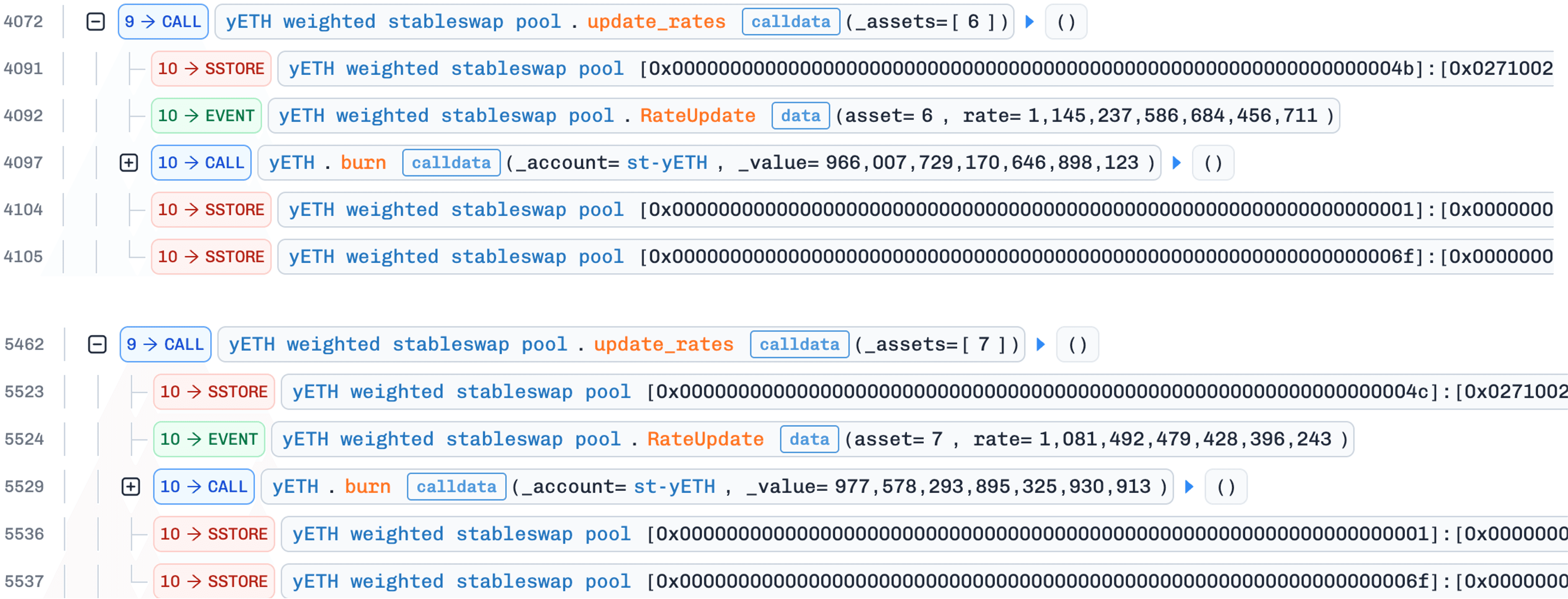
汇率差异本身并非利润来源；它仅作为触发机制。在三个池接口中，只有 add_liquidity() 和 update_rates() 调用 _calc_supply()；remove_liquidity() 使用比例缩放，不调用。在步骤 3 恢复非零乘积后，攻击者需要无需额外存入资产即可触发 _calc_supply()。调用一个汇率过时的 update_rates() 恰好实现了这一点：汇率变化触发供应重新计算，对攻击者零成本。

这解释了攻击中的一个微妙之处：在第一阶段（准备阶段），攻击者特意避免为 WOETH 和 mETH 添加流动性。如果在 add_liquidity() 期间更新了这些汇率，则不存在汇率差异，并且此步骤中的 update_rates() 不会触发 _calc_supply()。

5. 通过 `remove_liquidity()` 提取资产

在每个循环结束时，攻击者通过 remove_liquidity() 提取资产。

如何提取利润

利润机制如下：在步骤 1 中，攻击者存入 LST 并收到超额铸造的 yETH（由于乘积项被破坏）。在步骤 4 中，当供应量被纠正时，多余的 yETH 从 POL（质押合约）销毁，而不是从攻击者处销毁。在步骤 5 中，攻击者按其 yETH 持有量的比例提取 LST。由于 POL 吸收了销毁，而攻击者的 yETH 余额保持不变，攻击者最终提取的 LST 比存入的多。这个差额，通过三个循环提取，总计约 810 万美元。

Rebase 的目的

追踪（在第一次和第二次循环之间）还显示了一个调用 OETHVaultProxy.rebase() 的操作，该操作触发了一次 OETH rebase：WOETH 合约持有的 OETH 余额增加，提高了 WOETH 的有效汇率。这种“保存”的汇率差异使得第二次循环的步骤 4 再次成为可能：当最终调用 update_rates() 时，它检测到差异并触发 _calc_supply()。

耗尽至零

在重复此五步循环三次后，攻击者已将池的总供应量降至低于其持有的 yETH 数量。最后一次 remove_liquidity() 调用，用剩余的供应量，将其耗尽至零。

池现在持有零供应量、零乘积项和零 vb_sum。这种退化状态违反了池在之前存款后永远不会恢复到其未初始化状态的隐含设计假设。

0x3.3 第三阶段：利用零供应量获取额外利润（约 90 万美元）

目标： 从退化的池状态中铸造巨额 yETH，然后将其兑换成真实资产。此阶段利用了次要漏洞（未禁用的引导路径）和故障模式 B（下溢）的相互依赖组合，共同造成了约 10% 的总损失。

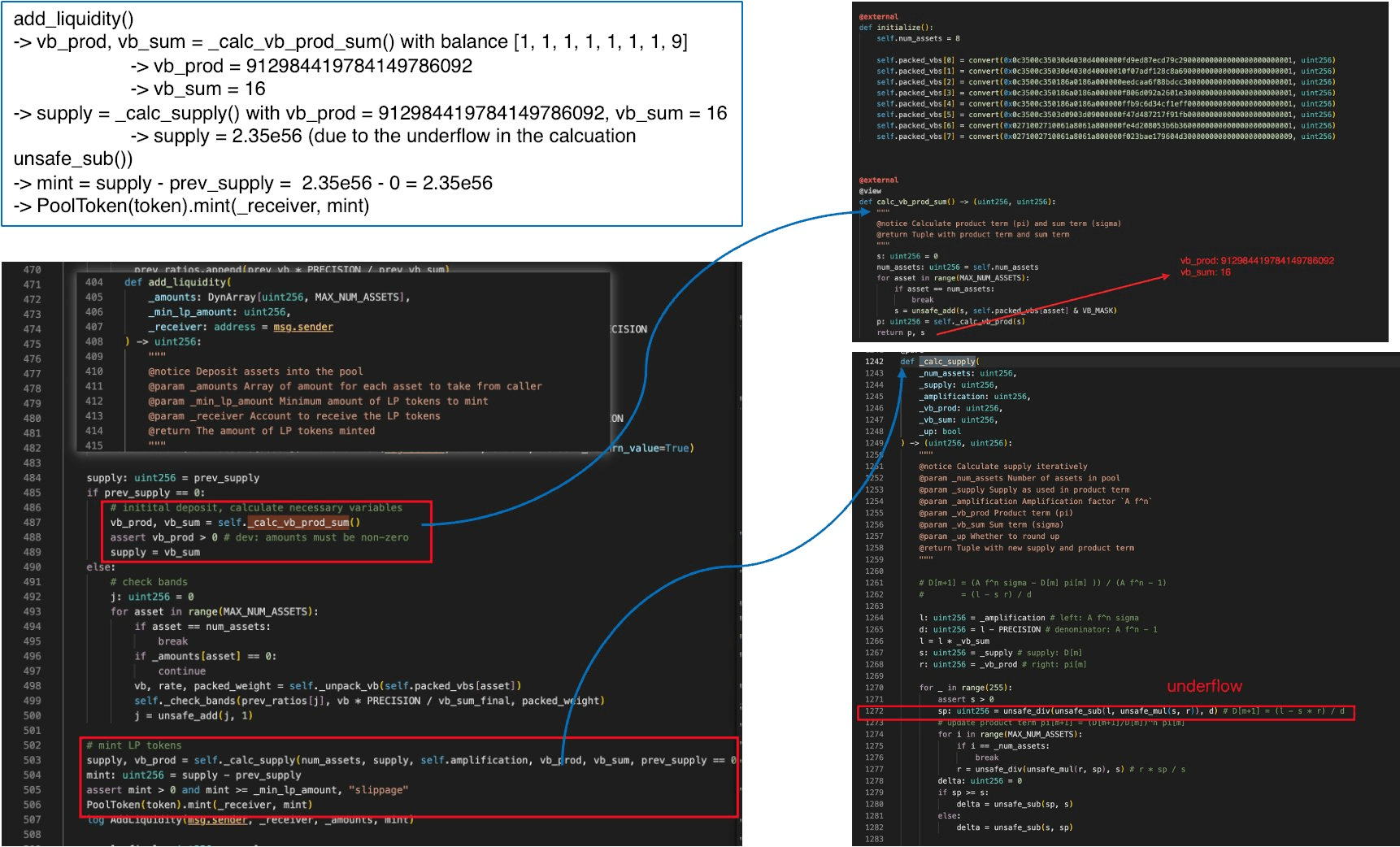
1. 通过下溢铸造

由于总供应量为零，攻击者调用 add_liquidity() 并传入粉尘金额（余额 [1, 1, 1, 1, 1, 1, 1, 9]）。

由于 prev_supply == 0，代码进入 0x2 节（根本原因分析）中描述的引导路径：它绕过存储状态，通过 _calc_vb_prod_sum() 从头开始重新计算 vb_prod 和 vb_sum，然后将这些值传入 _calc_supply()。这是第二个漏洞在起作用：攻击者已将池推回到其未初始化状态，从而获得了对输入到求解器的初始条件的控制权。

由于所有虚拟余额都为粉尘水平（汇率接近 1e18），计算出的值为：

• vb_sum = 16
• vb_prod ≈ 9.13e20
• _supply = vb_sum = 16

在 _calc_supply() 内部，变量初始化为：

• l = _amplification * _vb_sum ≈ 4.5e20 × 16 ≈ 7.2e21
• d = _amplification - PRECISION ≈ 4.49e20
• s = _supply = 16
• r = _vb_prod ≈ 9.13e20

现在进行减法 l - s * r：

$$7.2\times {10}^{21}-16\times 9.13\times {10}^{20}=7.2\times {10}^{21}-1.46\times {10}^{22}\approx -7.4\times {10}^{21}7.2\; \backslash times\; 10^\{21\}\; -\; 16\; \backslash times\; 9.13\; \backslash times\; 10^\{20\}\; =\; 7.2\; \backslash times\; 10^\{21\}\; -\; 1.46\; \backslash times\; 10^\{22\}\; \backslash approx\; -7.4\; \backslash times\; 10^\{21\}$$

这是负数。在未检查的 uint256 算术中，unsafe_sub 将其包装为约 $2^{256}-7.4\times {10}^{21}2^\{256\}\; -\; 7.4\; \backslash times\; 10^\{21\}$，一个天文数字。除以 d（约 4.49e20）后，得到的供应估计值约为 2.35e56，协议将所有这些数量铸造给了攻击者。只有因为第二阶段将总供应量降至零，才可能发生这种下溢；在任何非退化的池状态下，l > s * r 成立，减法是安全的。

2. 兑换成真实资产

攻击者将部分超额铸造的 yETH 在 yETH–WETH Curve 池中兑换成约 1,097e18 WETH，耗尽了该池的 WETH 储备。在扣除第一阶段花费的 800e18 WETH 后，净利润约为 90 万美元。

连同第二阶段提取的约 810 万美元 LST 资产，攻击者在偿还闪电贷后总计获得了约 900 万美元的总利润。

详细的资金流分析，包括资金来源和去向地址，已在其他已发表的分析中涵盖（例如 [2]），超出了本文的范围。

0x4 纠正误解

大多数已发表的对此次事件的分析侧重于算术症状，而没有完全解释攻击者如何设置先决条件。两个具体的说法值得纠正。

0x4.1 说法：“`pow_up()` 和 `pow_down()` 之间的舍入不匹配破坏了恒定值”

一种常见的解释将根本原因归结为某些代码路径中使用 pow_up() 而其他代码路径中使用 pow_down()，认为这种方向性不匹配引入了可利用的不一致性。

我们直接测试了这一点：我们修改了合约以统一使用 pow_down()（替换所有 pow_up() 调用），并在 Foundry 中重新运行了完整的攻击模拟。攻击成功地进行了，且结果完全相同。 乘积项仍然降至零，供应量仍然耗尽，下溢仍然产生膨胀的铸造。

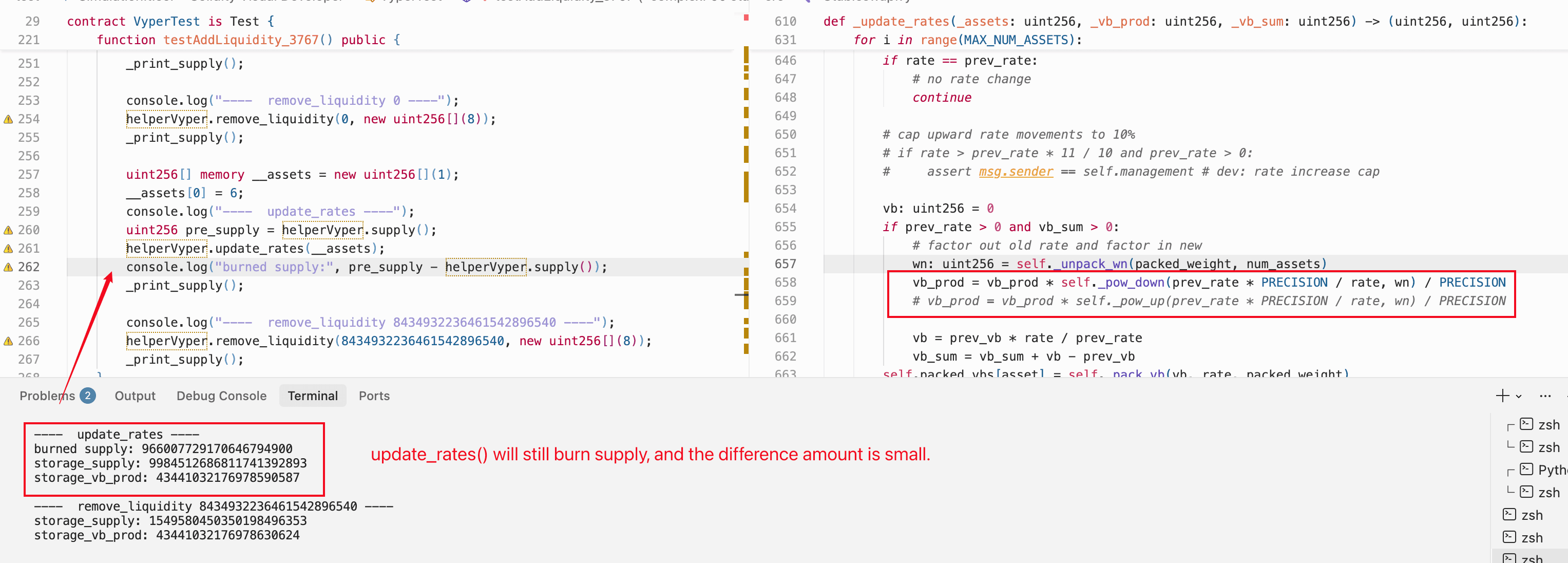
使零乘积状态成为可能的舍入是迭代循环内的**r = unsafe_div(unsafe_mul(r, sp), s) 中的地板除法，而不是用于估计初始乘积值的幂函数中的舍入方向。

0x4.2 说法：“第二次迭代中的下溢使中间项归零”

一个广泛引用的解释认为，在 _calc_supply() 的第二次迭代中，unsafe_sub 中的下溢产生了 sp ≈ 1.94e18，然后这导致 r 向下舍入为零。

我们使用 Foundry（链上回放）和 Python（数学验证）重现了精确的中间值。Foundry 模拟逐迭代地追踪 _calc_supply()：

======= _calc_supply iteration 0 =======
  l = 4905875511098192451202650000000000000000
  s = 2514373972590845290489        ← 初始供应量
  r = 3538247433646816               ← 初始乘积项（非常小）
  d = 4490000000000000000000

  sp = (l - s*r) / d ≈ 1.093e22     ← 新供应量跳升约 4 倍
  new r ≈ 4.49e22                    ← 乘积项急剧膨胀

======= _calc_supply iteration 1 =======
  s = 10926206313726454855296        ← 来自之前的 sp
  r = 44892226765713223838396        ← 来自之前的内循环

  sp = 19113493328251743069          ← ≈ 1.91e19，合法的小值
  new r = 0                          ← 舍入为零！

关键观察：在迭代 1 中，sp 的计算结果约为 1.91e19。这是一个合法的小正值，而不是下溢的产物。由于放大权重后的总和 l 和供应量-乘积项 s*r 在此迭代中数值接近，减法 l - s*r 产生了一个小的正结果。

导致乘积项归零的是接下来发生的事情：内循环计算 r = r * sp / s，其中 sp（约 1.91e19）远小于 s（约 1.09e22）。分子 r * sp 小于分母 s，整数除法将结果向下舍入为零。

我们通过 Python 独立验证了这一点，使用任意精度整数计算出相同的值，并确认减法没有发生下溢：

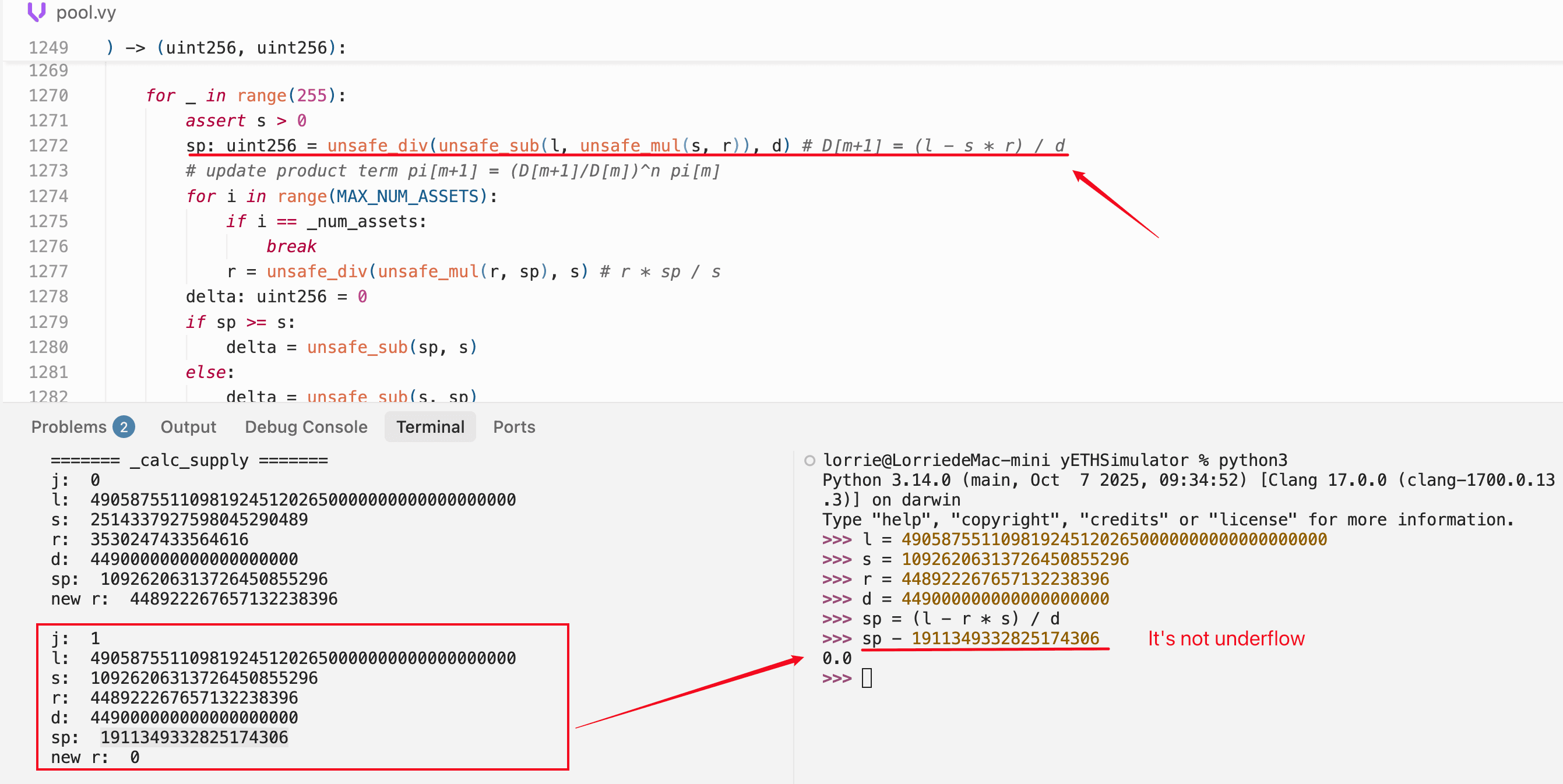
乘积项是由于除法中的舍入而归零，而不是由于减法中的下溢。导致供应量膨胀的 unsafe_sub 下溢发生在完全不同的上下文中：攻击的第三阶段，当粉尘流动性被添加到供应量降至零的池中时。

0x5 结论

yETH 漏洞利用涉及两个影响不对称的漏洞。不安全算术是主要根本原因：其向下舍入故障（故障模式 A）独立实现了约 810 万美元的损失，仅在第二阶段就已完成。未禁用的引导路径是次要漏洞；与下溢故障（故障模式 B）结合使用时，它在第三阶段额外实现了约 90 万美元的损失，但这仅发生在第二阶段已将供应量降至零之后。此损失细分区分了本次分析与其他已发表的报告，后者的报告未区分第二阶段和第三阶段的利润。

官方事后分析 [2] 确定了五个根本原因。我们将其重新归类为两个缺陷（不安全算术整合了官方的 #1 和 #5；未禁用的引导路径作为 #4）和两个架构先决条件（#2 不对称的 Π 处理；#3 POL 启用的零供应状态）。区别在于：缺陷是违反设计意图的实现错误（求解器不应产生零乘积或下溢），而先决条件是设计选择，当与缺陷结合时，它们会产生可利用的攻击面。

建议

• 恒定求解器中的已检查算术。 使用 safe_div 和 safe_sub，即使以牺牲 gas 效率为代价，也要显式回滚下溢/溢出。求解器最多运行 256 次迭代，gas 开销与安全风险相比微不足道。
• 中间值边界检查。 验证乘积项在迭代之间保持在合理范围内。乘积降至零或供应量在迭代之间增加几个数量级，都表明存在退化状态。
• 失衡限制。 强制执行任何资产的虚拟余额与其目标权重比例余额之间的最大偏差。这将阻止第一阶段产生先决条件。
• 恒定单调性检查。 _calc_supply() 返回后，验证新供应量是否与变化方向一致（例如，增加流动性绝不应减少供应量，汇率更新不应产生 10 倍的变化等）。
• 永久禁用初始化路径。 池首次存款后，限制 prev_supply == 0 引导路径，使其无法重新进入。这将完全阻止第三阶段。
• 防止零供应状态。 确保协议级别的销毁（来自 POL 或质押合约）不能在池持有非零余额时将总供应量降至零。最低供应地板将阻止向导致引导重新进入的退化状态的过渡。
• 实时异常检测。 监控异常状态转换（例如，乘积项降至零、供应量变化几个数量级，或短时间内重复的添加/移除循环），并在损失累积之前触发警报或熔断器。

参考资料

1. Yearn Finance 事件公告
2. Yearn 安全事后分析
3. yETH 文档
4. yETH 白皮书：恒定值推导
5. BlockSec Explorer 上的攻击交易
6. BlockSec：对 Balancer 增强池事件的分析（2023 年 8 月）

关于 BlockSec

BlockSec 是一个全栈区块链安全和加密合规提供商。我们构建产品和服务，帮助客户在协议和平台的整个生命周期内进行代码审计（包括智能合约、区块链和钱包）、实时拦截攻击、分析事件、追踪非法资金，并满足 AML/CFT 要求。

BlockSec 在享有盛誉的会议上发表了多篇区块链安全论文，报告了 DeFi 应用的数起零日攻击，阻止了多次黑客攻击以挽救超过 2000 万美元，并保障了数十亿美元的加密货币。

• 官方网站：https://blocksec.com/

• 官方 Twitter 账号：https://twitter.com/BlockSecTeam

• 🔗 BlockSec 审计服务 : 提交请求

• 🔗 Phalcon 安全 APP: 预订演示

• 🔗 Phalcon 合规