#10 全景事件：XOR线性破坏位置指纹方案

2025年8月25日，在Cantina和Seal911的协助下，Panoptic进行了一次白帽救援行动，挽回了约40万美元的风险资金[1]。根本原因是s_positionsHash构建中的一个缺陷：协议使用XOR来聚合位置ID的Keccak256哈希值，形成一个单一的指纹。虽然单个Keccak256哈希值保持抗碰撞性，但XOR的数学线性使其复合指纹不安全。攻击者可以生成一组伪造的位置ID，其XOR聚合哈希值与任何目标指纹匹配，从而绕过协议的位置验证，在不偿还债务的情况下提取抵押品。

背景

Panoptic是一个构建在以太坊上的去中心化永续期权交易协议，使用户能够交易看跌期权和看涨期权。

withdraw()函数有一个输入参数positionList，它由一组tokenId组成。每个tokenId代表一个仓位。withdraw()函数根据s_positionsHash检查每个仓位的债务状况，然后检索用户的抵押品。

为了节省Gas，协议不存储用户的每个仓位（即tokenId）。相反，它根据用户的所有tokenId计算一个指纹，并将其记录在s_positionsHash中。每个s_positionsHash的最高8位代表numLegs，而低248位代表user position hash。

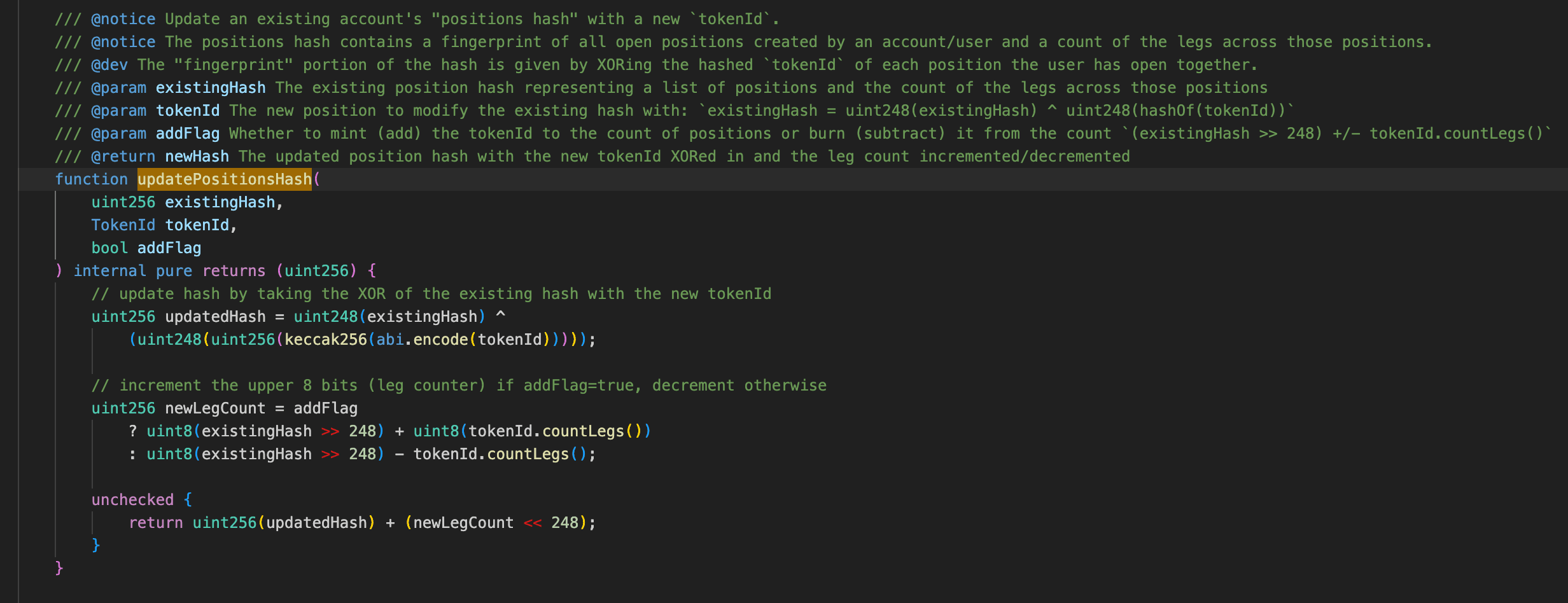
对于每个传入的tokenId，协议会计算其哈希值，取低248位，并通过与当前s_positionsHash的低248位进行按位XOR运算来更新user position hash。

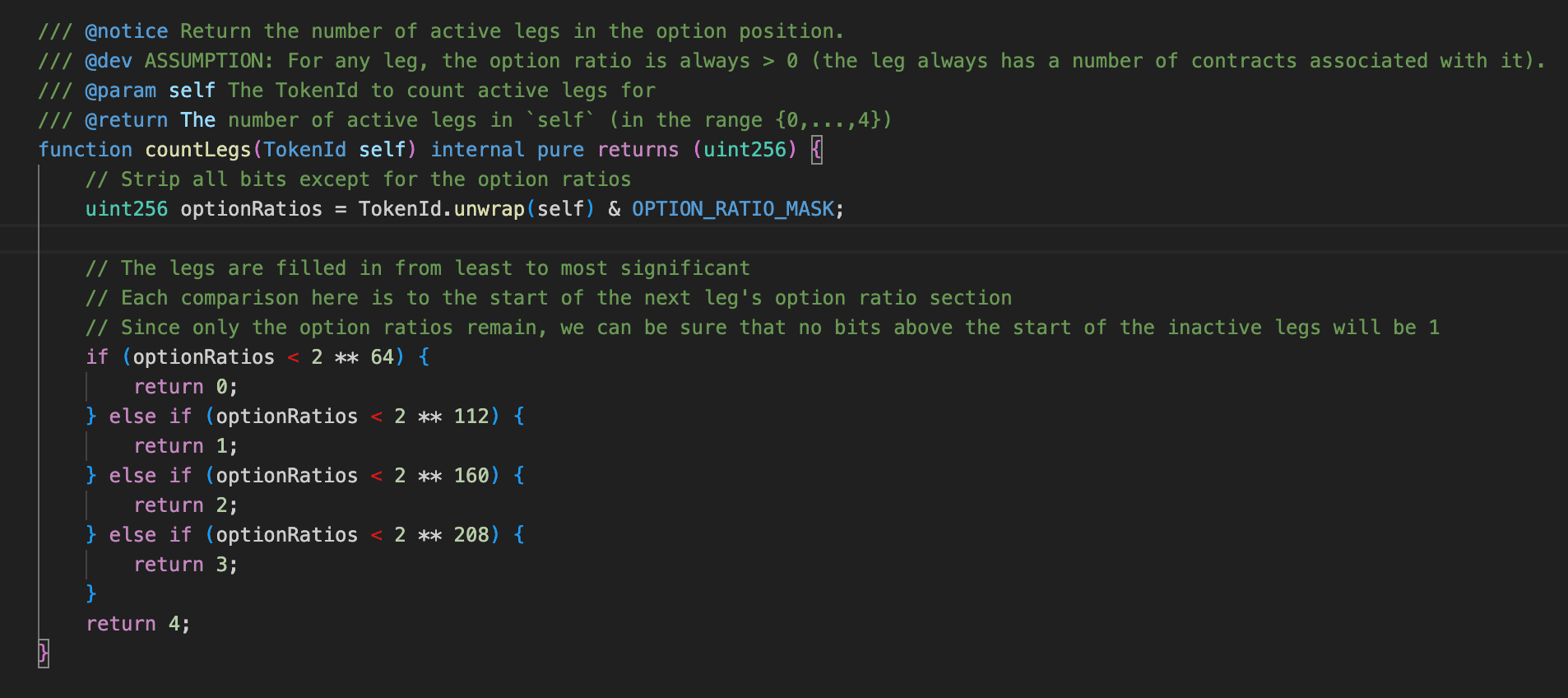
同时，countLegs会根据tokenId的数值范围进行调整：当tokenId小于$2^{64}2^\{64\}$时，它保持不变；当tokenId在$(2^{64},2^{112})(2^\{64\},\; 2^\{112\})$、$(2^{112},2^{168})(2^\{112\},\; 2^\{168\})$和$(2^{168},2^{208})(2^\{168\},\; 2^\{208\})$的范围内时，它分别增加1、2或3。最后，这些值被写入s_positionsHash的最高8位以更新numLegs。

漏洞分析

根本原因是合约构建s_positionsHash的算法存在缺陷，特别是使用XOR操作来聚合Keccak256哈希结果。虽然单个哈希函数是安全的，但XOR操作的数学线性使得整体指纹算法（即哈希值的XOR和）不安全[2]。

线性意味着攻击者不需要破解哈希函数本身（即从哈希值反向推导tokenId）。相反，他们可以采用组合策略：生成大量随机tokenId，计算它们的Keccak256(tokenId)，然后从这些哈希值中选择一个特定的子集，使得这些tokenId哈希值的XOR和正好等于受害者的目标指纹。

这使得攻击者在调用withdraw()时可以传递一组伪造的tokenId，从而通过健康检查并提取对应于s_positionsHash的所有抵押品。

理论

假设用户的仓位指纹s_positionsHash具有user position hash $TT$ 和numLegs $kk$，以及用户tokenId $\{t_1,t_2,\dots ,t_n\}\backslash \{t\_1,\; t\_2,\; \backslash dots,\; t\_n\backslash \}$。因此：

$$\underset{i=1}{\overset{k}{⨁}}[\text{Hash}(t_i)(\mathrm{m}\mathrm{o}\mathrm{d}{2}^{248})]=T\backslash bigoplus\_\{i=1\}^\{k\}\; [\backslash text\{Hash\}(t\_i)\; \backslash pmod\{2^\{248\}\}]\; =\; T$$

这里，每个248位的哈希值都可以看作一个248维的向量。

$$\text{Hash}(t_i)(\mathrm{m}\mathrm{o}\mathrm{d}{2}^{248})=[b_0,b_1,\dots ,b_{247}{]}^T,\text{其中 }{b}_i\in \{0,1\}\backslash text\{Hash\}(t\_i)\; \backslash pmod\{2^\{248\}\}\; =\; [b\_0,\; b\_1,\; \backslash dots,\; b\_\{247\}]^T,\; 其中\backslash \; b\_i\; \backslash in\; \backslash \{0,\; 1\backslash \}$$

因此，$TT$存在于一个由0和1组成的248维空间（${\mathbb{F}}_2^{248}\backslash mathbb\{F\}\_2^\{248\}$）中。在这个空间中，XOR操作等同于向量加法（附录I）。

攻击者的目标是找到$nn$个248维向量$\{v_1,v_2,\dots ,v_n\}\backslash \{v\_1,\; v\_2,\; \backslash dots,\; v\_n\backslash \}$，使得它们的XOR和的低248位等于$TT$。因此，我们可以将攻击者的目标表述为一个线性方程组：

$$x_1{v}_1+x_2{v}_2+\cdots +x_n{v}_n=Tx\_1\; v\_1\; +\; x\_2\; v\_2\; +\; \backslash dots\; +\; x\_n\; v\_n\; =\; T$$

具体来说，我们不需要直接尝试构造$TT$。相反，我们选择$nn$个线性无关的哈希向量$\{v_1,v_2,\dots ,v_n\}\backslash \{v\_1,\; v\_2,\; \backslash dots,\; v\_n\backslash \}$（其中$nn$等于维度248），并将它们作为列向量来构建一个$n\times nn\; \backslash times\; n$的矩阵$AA$：

$$A=[v_1,v_2,\dots ,v_n]A\; =\; [v\_1,\; v\_2,\; \backslash dots,\; v\_n]$$

问题则转化为寻找一个系数向量$xx$，使得：

$$A\cdot x=TA\; \backslash cdot\; x\; =\; T$$

其中 $x=[x_1,x_2,\dots ,x_n{]}^{T}x\; =\; [x\_1,\; x\_2,\; \backslash dots,\; x\_n]^T$，且 $x_i\in \{0,1\}x\_i\; \backslash in\; \backslash \{0,\; 1\backslash \}$。

根据线性代数理论，只要矩阵$AA$是满秩的，它就张成了整个$nn$维空间。这意味着对于任何目标$TT$，方程组都有唯一解。求解$xx$后，我们只需保留那些$x_i=1x\_i=1$的向量$v_{i}v\_i$；它们的XOR和就是$TT$。

示例

为了便于理解，我们用一个案例研究来演示这个构建过程。假设向量是3维的，每个维度只包含0或1，目标哈希值为101，即 $T=[1,0,1{]}^{T}T\; =\; [1,\; 0,\; 1]^T$。

接下来，我们随机生成3个哈希值：

• $v_1=[1,1,0{]}^{T}v\_1\; =\; [1,\; 1,\; 0]^T$
• $v_2=[0,1,0{]}^{T}v\_2\; =\; [0,\; 1,\; 0]^T$
• $v_3=[0,1,1{]}^{T}v\_3\; =\; [0,\; 1,\; 1]^T$

我们使用这三个向量作为列来构建矩阵$AA$，并建立方程$Ax=TAx=T$：

通过高斯消元法求解，我们得到 $x=[1,0,1{]}^{T}x\; =\; [1,\; 0,\; 1]^T$。这意味着我们需要选择$v_{1}v\_1$和$v_{3}v\_3$（对应于$x_1=1,x_3=1x\_1=1,\; x\_3=1$），它们的XOR和正好等于目标$TT$。

选择n个线性无关的向量

如前所述，为了求解$Ax=TAx=T$，我们需要构建一个满秩矩阵$AA$。考虑到我们处理的是一个非常大的向量空间（$m=2^{248}m\; =\; 2^\{248\}$），核心问题是：如何快速地从这个巨大的空间中选择$nn$个线性无关的向量？

考虑最简单的方法：随机生成$nn$个tokenId并选择它们的哈希结果作为向量。

在${\mathbb{F}}_2\backslash mathbb\{F\}\_2$上，$nn$个随机选择的$nn$维向量构成满秩矩阵的概率$PP$为：

$$P(n)=\prod _{k=0}^{n-1}(1-\frac{2^k}{2^n})P(n)\; =\; \backslash prod\_\{k=0\}^\{n-1\}\; \backslash left(1\; -\; \backslash frac\{2^k\}\{2^n\}\backslash right)$$

当$nn$很大时（在此示例中，$n=248n=248$），此概率收敛到一个常数（附录II）：

$$\underset{n\to \mathrm{\infty }}{\lim }P(n)\approx 0.28879\backslash lim\_\{n\; \backslash to\; \backslash infty\}\; P(n)\; \backslash approx\; 0.28879$$

这意味着每次随机尝试大约有**28.9%**的成功概率。平均而言，攻击者只需要大约3.5次尝试即可找到一组线性无关的向量。因此，计算成本极低，攻击者可以快速构建一个满足条件的矩阵$AA$。

为了控制最高8位的countLegs，我们只需要根据目标countLegs调整随机生成的tokenId值的范围。

例如，如果我们希望伪造指纹中的numLegs为0，我们只需确保随机生成的$nn$个tokenId都小于$2^{64}2^\{64\}$。由于此范围内的tokenId的leg增量为0，无论高斯消元解$xx$选择哪个向量，最终累积的numLegs都将不可避免地为0。

攻击分析

白帽救援者发起了多次救援交易。为简化起见，以下讨论基于其中一笔交易[3]。

核心逻辑包含以下5个步骤：

1. 通过Aave的闪贷借入0.23e8 WBTC和28e18 WETH。
2. 将0.23e8 WBTC和28e18 WETH存入poWBTC合约和0x1f8d_poWETH合约。
3. 调用PanopticPool合约的mintOptions()，使用一个正常的positionIdList来借入资金并开立杠杆头寸。
4. 调用withdraw()，传入伪造的tokenId。由于这些伪造的头寸positionSize为0，该函数返回的tokenRequired为0，这意味着所有头寸所需总抵押品被错误地计算为零。与此同时，这些tokenId生成的s_positionsHash与步骤3中生成的完全相同，使得救援者可以在不偿还任何债务的情况下提取所有抵押品。
5. 偿还闪贷并执行下一轮。

总结

此次事件暴露了两个复合缺陷，共同导致了未经授权的抵押品提取。

• XOR不是安全的哈希聚合函数。 Keccak256是抗碰撞的，但XOR的线性意味着多个哈希值的XOR和不会继承该属性。构造一组输入，其哈希值XOR得到任何目标值，就归结为在${\mathbb{F}}_2\backslash mathbb\{F\}\_2$上求解一个线性方程组，这是计算上微不足道的。哈希组合需要执行保留抗碰撞性的操作，例如连接后重新哈希。
• 仓位ID验证缺失。 该协议未验证传入的positionId是否对应于有效的期权仓位。小于$2^{64}2^\{64\}$的值带有0的countLegs和0的positionSize，意味着伪造的仓位不会产生任何债务。这使得攻击者可以用零抵押品需求通过健康检查，同时匹配目标指纹。

参考

1. https://x.com/Panoptic_xyz/status/1961187739866644524

2. https://cseweb.ucsd.edu/~mihir/papers/inchash.pdf

3. https://app.blocksec.com/explorer/tx/eth/0x67a45dfe5ff4b190058674d7c791bbdc48e889f319f937c24fa13a5f9093f088

附录

以下两个附录提供了对正文陈述的数学解释和证明，即XOR运算等同于向量加法（附录I），以及随机矩阵满秩的概率（附录II）。

附录I

在有限域${\mathbb{F}}_2=\{0,1\}\backslash mathbb\{F\}\_2\; =\; \backslash \{0,\; 1\backslash \}$中，加法定义为模2加法：

观察表明，这与异或（XOR，符号$\oplus \backslash oplus$）逻辑运算完全相同。

对于$nn$维向量空间${\mathbb{F}}_2^n\backslash mathbb\{F\}\_2^n$（在此例中为$n=248n=248$），两个向量$u=[u_1,\dots ,u_n{]}^{T}u\; =\; [u\_1,\; \backslash dots,\; u\_n]^T$和$v=[v_1,\dots ,v_n{]}^{T}v\; =\; [v\_1,\; \backslash dots,\; v\_n]^T$的加法定义为分量模2加法：

$$u+v=\left[\begin{array}{c}{u}_1+v_1(\mathrm{m}\mathrm{o}\mathrm{d}2)\\ \mathrm{⋮}\\ u_n+v_n(\mathrm{m}\mathrm{o}\mathrm{d}2)\end{array}\right]=\left[\begin{array}{c}{u}_1\oplus v_1\\ \mathrm{⋮}\\ u_n\oplus v_n\end{array}\right]=u\oplus vu\; +\; v\; =\; \backslash begin\{bmatrix\}\; u\_1\; +\; v\_1\; \backslash pmod\; 2\; \backslash \backslash \; \backslash vdots\; \backslash \backslash \; u\_n\; +\; v\_n\; \backslash pmod\; 2\; \backslash end\{bmatrix\}\; =\; \backslash begin\{bmatrix\}\; u\_1\; \backslash oplus\; v\_1\; \backslash \backslash \; \backslash vdots\; \backslash \backslash \; u\_n\; \backslash oplus\; v\_n\; \backslash end\{bmatrix\}\; =\; u\; \backslash oplus\; v$$

因此，在${\mathbb{F}}_2^n\backslash mathbb\{F\}\_2^\{n\}$向量空间中，向量加法等同于向量分量的按位XOR运算。

附录II

为了使矩阵满秩，这$nn$个向量必须是线性无关的。

第一个向量$v_{1}v\_1$可以是${\mathbb{F}}_2^n\backslash mathbb\{F\}\_2^n$中的任意非零向量，提供$2^n-12^n\; -\; 1$种选择；第二个向量$v_{2}v\_2$不能存在于$\{v_1\}\backslash \{v\_1\backslash \}$张成的子空间中，该子空间包含$2^{1}2^1$个向量，剩下$2^n-22^n\; -\; 2$种选择；按照这个逻辑，第$kk$个向量$v_{k}v\_k$不能存在于前$k-1k-1$个向量张成的子空间中，导致有$2^n-2^{k-1}2^n\; -\; 2^\{k-1\}$种可能选择。

这样的矩阵（即$GL(n,{\mathbb{F}}_2)GL(n,\; \backslash mathbb\{F\}\_2)$的阶数）总数为：

$$N=\prod _{k=0}^{n-1}(2^n-2^k)=(2^n-1)(2^n-2)(2^n-4)\cdots (2^n-2^{n-1})N\; =\; \backslash prod\_\{k=0\}^\{n-1\}\; (2^n\; -\; 2^k)\; =\; (2^n\; -\; 1)(2^n\; -\; 2)(2^n\; -\; 4)\backslash cdots(2^n\; -\; 2^\{n-1\})$$

而所有可能的$n\times nn\; \backslash times\; n$矩阵的总数为 $(2^n{)}^n=2^{n^2}(2^n)^n\; =\; 2^\{n^2\}$。

因此，概率$PP$为：

$$P=\frac{\prod _{k=0}^{n-1}(2^n-2^k)}{2^{n^2}}=\prod _{k=0}^{n-1}\left(\frac{2^n-2^k}{2^n}\right)=\prod _{k=0}^{n-1}(1-\frac{2^k}{2^n})P\; =\; \backslash frac\{\backslash prod\_\{k=0\}^\{n-1\}\; (2^n\; -\; 2^k)\}\{2^\{n^2\}\}\; =\; \backslash prod\_\{k=0\}^\{n-1\}\; \backslash left(\; \backslash frac\{2^n\; -\; 2^k\}\{2^n\}\; \backslash right)\; =\; \backslash prod\_\{k=0\}^\{n-1\}\; (1\; -\; \backslash frac\{2^k\}\{2^n\})$$

令 $j=n-kj\; =\; n\; -\; k$，我们可以将此表达式重写为：

$$P=\prod _{j=1}^n(1-\frac{1}{2^j})P\; =\; \backslash prod\_\{j=1\}^\{n\}\; \backslash left(1\; -\; \backslash frac\{1\}\{2^j\}\backslash right)$$

当 $n\to \mathrm{\infty }n\; \backslash to\; \backslash infty$时，该乘积收敛到一个常数：

$$P\approx 0.288788P\; \backslash approx\; 0.288788$$

这意味着对于大的$nn$，随机矩阵满秩的概率约为28.9%。

关于BlockSec

BlockSec是一家全栈区块链安全与加密合规提供商。我们构建产品和服务，帮助客户在协议和平台的整个生命周期中进行代码审计（包括智能合约、区块链和钱包）、实时拦截攻击、分析事件、追踪非法资金，并满足AML/CFT合规要求。

BlockSec在顶级会议上发表了多篇区块链安全论文，报告了多起DeFi应用的零日攻击，阻止了多次黑客攻击挽回了超过2000万美元，并保护了数十亿美元的加密货币。

• 官方网站：https://blocksec.com/

• 官方Twitter账号：https://twitter.com/BlockSecTeam

• 🔗 BlockSec审计服务: 提交请求

• 🔗 Phalcon安全APP: 预约演示

• 🔗 Phalcon合规