#5 Yearn Finance事件：不変ソルバーの安全でない算術演算がその名を汚す

2025年11月30日、Yearn FinanceのyETH Weighted Stable Poolが900万ドル以上を不正流用されました[1]。根本原因は、不安全な算術演算がインバリアントソルバー _calc_supply() に存在したこと、および初期化ロジックへの再エントリを許容する無効化されていないブートストラップパスでした。公式の事後分析[2]では、5つの項目が根本原因として挙げられていますが、これらは2つの欠陥（上記の脆弱性）と、これらの欠陥が存在する状況でのみ悪用可能になった2つのアーキテクチャ上の事前条件に再分類できます。他の利用可能な分析は、攻撃トランザクションの詳細なステップバイステップに焦点を当てています。高レベルの概要とトランザクションレベルの詳細の間にはギャップがあります。攻撃はどのように、そしてなぜ実際に機能したのでしょうか？この記事は、FoundryとPythonシミュレーションを使用して、主要な値がどのようにステップバイステップで進化し、計算がどこで破綻するかを追跡することにより、そのギャップを埋めます。

この分析は、主に以下の3つの貢献をしています。

1. 脆弱性ごとの損失の内訳。 2つの脆弱性は相互依存していません。不安全な算術演算だけで約810万ドル（総額の90％）の損失が発生し、ブートストラップパスが追加で約90万ドルの損失を可能にしました。これにより、どちらの脆弱性が主であったかが明確になります。
2. 根本原因の再分類。 公式レポートの5つの根本原因は、2つの実装上の欠陥（5項目のうち3項目を統合）と、欠陥と組み合わされた場合にのみ悪用可能になった2つのアーキテクチャ上の事前条件として理解する方が適切です。
3. 技術的な誤解の修正。 「2回目の反復でのアンダーフローが積項をゼロにする」という主張は成り立ちません。シミュレーションによると、積はアンダーフローではなく、除算における丸めによってゼロになり、利益を生むアンダーフローは完全に異なるフェーズで発生します。

この記事の残りは、以下のように構成されています。セクション0x1では、yETHのWeighted Stable Poolとインバリアントソルバーの背景について説明します。セクション0x2では、2つの根本原因とその障害モードを分析します。セクション0x3では、3フェーズの攻撃を詳細に追跡します。セクション0x4では、シミュレーション証拠を用いて2つの一般的な誤解を修正します。セクション0x5では、推奨事項で締めくくります。

TL;DR

根本原因： 2つの脆弱性が悪用されましたが、影響は非対称でした。

1. _calc_supply() の不安全な算術演算（主、〜810万ドル）。プール状態からyETH供給を再計算する関数には、2つの算術的障害があります。unsafe_div() の切り捨て丸めは内部積項をゼロにすることができ、unsafe_sub() のアンダーフローは中間値を巨大な正の整数にラップさせることができます。この脆弱性だけでも、yETH Weighted Stableswap Poolを空にするのに十分でした。
2. 無効化されていないブートストラップパス（副、〜90万ドル）。prev_supply == 0 の初期化ブランチは、デプロイ後も恒久的にゲートされませんでした。最初の脆弱性によって供給がゼロにされた後、このパスに到達可能になり、yETH/WETH Curve Poolからの追加利益が可能になりました。

不安全な算術演算の脆弱性内では、切り捨て丸め障害（障害モードA）のみがフェーズ2で使用されました（〜810万ドル）。アンダーフロー障害（障害モードB）はブートストラップパスと相互依存しており、それらが組み合わさってフェーズ3を可能にしました。

攻撃者は3フェーズのシーケンスを実行しました。

1. 準備： 仮想残高の極端な不均衡を作成するために、繰り返しの追加/削除サイクルを通じてプールの資産配分を歪める。
2. 供給操作： _calc_supply() の切り捨て丸めを悪用して積項をゼロに崩壊させ、その後、一連のミント/バーン操作を通じて総供給をゼロにする。すべてのプールのLSTが引き出され、WETHにスワップされた結果、〜810万ドルの損失が発生した。
3. 利益抽出： ダスト堆積物でブートストラップパス（prev_supply == 0）をトリガーし、_calc_supply() のアンダーフローを悪用して約2.35×10^56 yETHをミントし、それらを使用してyETH/WETH Curve Poolを空にし、〜90万ドルの損失につながった。

修正された2つの一般的な誤解：

• 「pow_up() と pow_down() が異なる丸めを行うため、インバリアントが破綻する。」 Foundryシミュレーションでpow_up()をpow_down()に置き換えることで検証しました。エクスプロイトは依然として機能します。丸め不一致は根本原因ではありません。
• 「2回目の反復でのアンダーフローが中間項をゼロにする。」 FoundryとPythonのシミュレーションは、2回目の反復でアンダーフローが発生しないことを示しています。実際の値は約1.91e19（主張されている〜1.94e18ではない）であり、正しい減算の正当な結果です。積がゼロになるのは、その後の除算での切り捨て丸めであり、アンダーフローではありません。

0x1 背景

このインシデントで資産を失ったプールは2つです：yETH Weighted StableSwap Pool（LSTを保有するYearnプール、〜810万ドルの損失）とyETH/WETH Curve Pool（Curve StableSwap Pool、〜90万ドルの損失）。yETH Weighted StableSwap Poolが、中心的な脆弱性が存在する場所です。このセクションでは、脆弱性とエクスプロイトを理解するために必要な背景情報を提供します。

0x1.1 仮想残高とインバリアント

yETHプロトコルは、Ethereum Liquid Staking Tokens（LST）のAutomated Market Maker（AMM）です[3]。影響を受けたyETH Weighted StableSwap Poolは、複数のLSTを単一のプールに集約します。ユーザーはLSTを預け入れ、プールシェアトークンとしてyETHを受け取ります。

各LSTは、時間とともに報酬を蓄積するステーキングされたETHを表すため、ベースETHに対する交換レートが変化します。会計を統一するために、プールは各資産の仮想残高 $x_{i}x\_i$ を定義します：オンチェーン残高 × 交換レート。これにより、すべての資産がビーコンチェーンETH単位に正規化されます。すべての仮想残高の合計は $\sigma =\sum x_i\backslash sigma\; =\; \backslash sum\; x\_i$ で表されます。

プールには8つの資産（インデックス0〜7）が含まれており、それぞれに指定された重み $w_{i}w\_i$ があります。

プールの状態は、重み付きStableSwapスタイルのインバリアントによって管理されます[4]。

$$\begin{array}{cccc}& {Af}^n\sigma +D={Af}^{n}D+D\cdot \pi & & \text{(1)}\end{array}\backslash mathit\{Af\}^\{\backslash ,n\}\backslash ;\backslash sigma\; +\; D\; =\; \backslash mathit\{Af\}^\{\backslash ,n\}\backslash ;D\; +\; D\; \backslash cdot\; \backslash pi\; \backslash tag\{1\}$$

ここで：

• $DD$ はインバリアントスケールであり、このプール全体の総yETH供給に直接等しくなります。プールが完全にバランスしている場合、$D=\sigma D\; =\; \backslash sigma$ です。
• $\pi \backslash pi$ は重み付き積項であり、$\pi =D^n{\prod }_i{\left(\frac{w_i}{x_i}\right)}^{v_i}\backslash pi\; =\; D^n\; \backslash prod\_\{i\}\; \backslash left(\backslash frac\{w\_i\}\{x\_i\}\backslash right)^\{v\_i\}$ と定義されます。ここで、$w_{i}w\_i$ は資産 i の重み、$v_i=w_i\cdot nv\_i\; =\; w\_i\; \backslash cdot\; n$ です。
• $Af\backslash mathit\{Af\}$ は増幅係数であり、単一のプロトコルパラメータです（$A\times fA\; \backslash times\; f$ ではありません）。${Af}^n\backslash mathit\{Af\}^\{\backslash ,n\}$ はこの係数に $nn$ を乗じたものを表します。ここで、$nn$ は資産数（このプールでは8）です。これは、均衡付近の定数和と極端での定数積の間の曲線の形状を制御します。

重要な特性：$DD$ には閉形式解がありません。数値的に解決する必要があります。そのソルバー、_calc_supply() が算術脆弱性が存在する場所です。

0x1.2 インバリアントソルバー

プロトコルは、256回の反復で制限された不動点反復により $DD$ を再計算します。このアルゴリズムはコード内の _calc_supply() として実装されています（セクション0x2.1で詳細）。各反復は3つのステップを実行します。

ステップ1：供給推定値の更新。

$$\begin{array}{cccc}& D_{m+1}=\frac{{Af}^n\cdot \sigma -D_m\cdot {\pi }_m}{{Af}^n-1}& & \text{(2)}\end{array}D\_\{m+1\}\; =\; \backslash frac\{\backslash mathit\{Af\}^\{\backslash ,n\}\; \backslash cdot\; \backslash sigma\; -\; D\_m\; \backslash cdot\; \backslash pi\_m\}\{\backslash mathit\{Af\}^\{\backslash ,n\}\; -\; 1\}\; \backslash tag\{2\}$$

ステップ2：新しい供給に一致するように積項を更新。

$$\begin{array}{cccc}& {\pi }_{m+1}={\pi }_m\cdot {\left(\frac{D_{m+1}}{D_m}\right)}^n& & \text{(3)}\end{array}\backslash pi\_\{m+1\}\; =\; \backslash pi\_m\; \backslash cdot\; \backslash left(\backslash frac\{D\_\{m+1\}\}\{D\_m\}\backslash right)^n\; \backslash tag\{3\}$$

ステップ3：収束の確認。

ならば $D_{m}D\_\{m\}$ を返します。そうでなければステップ1から繰り返します。

初期値 $D_{0}D\_0$、${\pi }_0\backslash pi\_0$、および $\sigma \backslash sigma$ は初期反復に影響を与えます。理論的には最終的な収束には無関係ですが、有限の反復と固定小数点演算のため実際の結果に影響します。

実装では、固定小数点整数演算が使用されます。除算は切り捨てられ、減算はアンダーフローをガードしません。通常のプール条件下では、中間値は安全な範囲内に留まります。極端なプール状態では、そうはなりません。セクション0x2.1では、これらの障害モードを詳細に分析します。

0x1.3 3つのインターフェースとインバリアントソルバー

プロトコルは、重み付き積項 $\pi \backslash pi$（コードでは vb_prod として保存）を更新することにより、プール状態に影響を与える3つのエントリーポイントを公開します。

非対称性は重要です。add_liquidity() は任意の比率の預け入れを許可しますが（プールを大幅に歪めることができます）、remove_liquidity() は常に比例して引き出します。したがって、追加/削除の繰り返しサイクルは、プールをますます不均衡な状態にラチェットさせることができます。

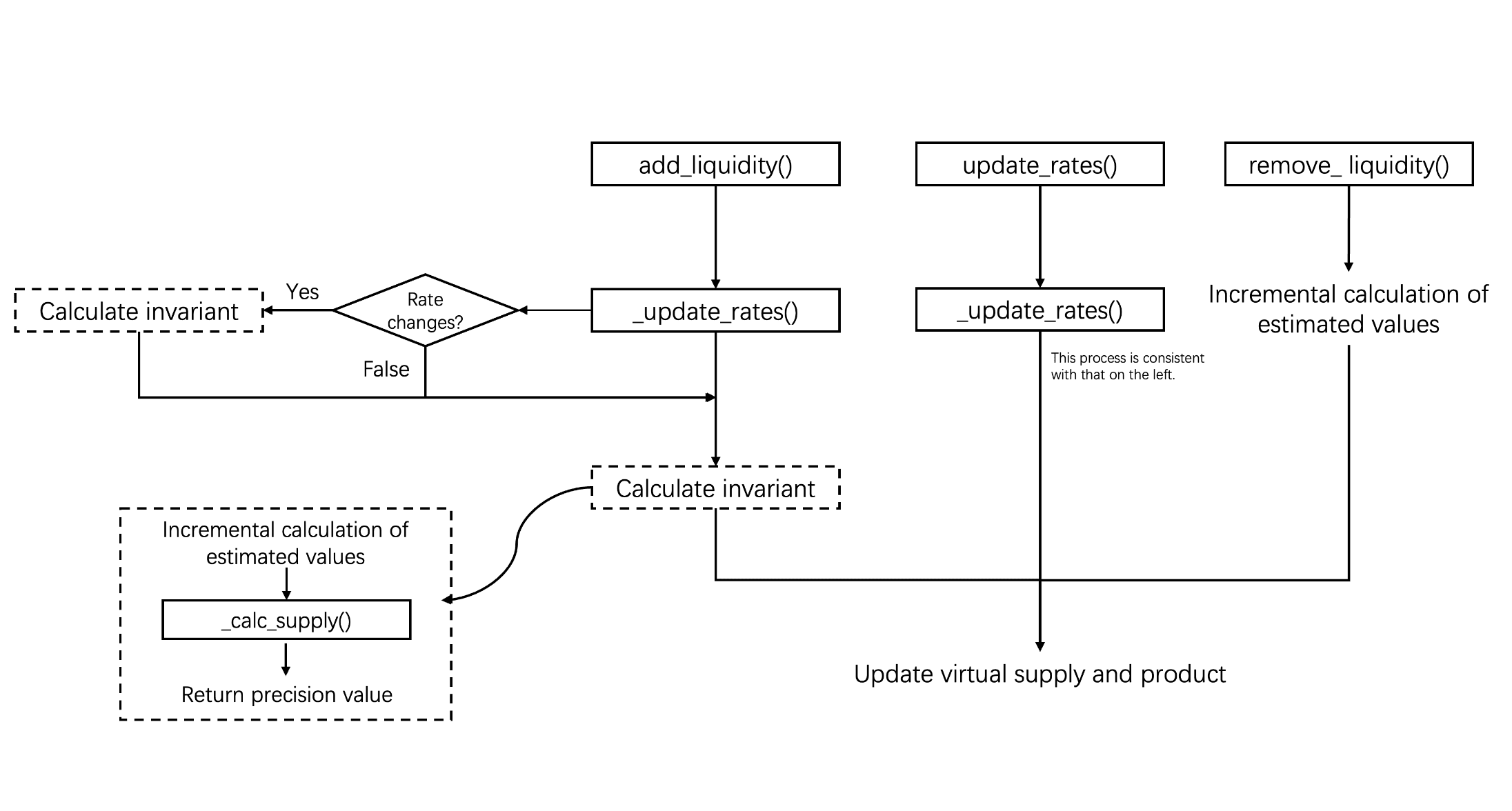
レート更新のメカニズム

前述のように、仮想残高（$x_{i}x\_i$）はLSTの交換レートに基づいて計算されます。したがって、レートを更新する方法を理解することが重要です。

具体的には、add_liquidity() および update_rates() 関数は、内部関数 _update_rates() を介してレートを更新できますが、remove_liquidity() 関数はレート同期を実行しません。

• add_liquidity() は、重要な操作を実行する前に _update_rates() を呼び出し、資産交換レートが最新の状態に同期されていることを確認します。
• update_rates() は、手動のレート更新を許可します。

_update_rates() 関数は、コントラクト内に記録された交換レートが外部レートと一致しているかどうかを確認します。不一致が検出された場合、仮想残高の再計算をトリガーし、その後インバリアントを更新します。そうでなければ、更新プロセスはスキップされます。

各インターフェースが $\pi$ を処理する方法

インバリアントに影響を与える方法に基づいて、これら3つの関数は2つのカテゴリに分類できます。具体的には、add_liquidity() と update_rates() は仮想残高の非比例的な変更を許可するため、供給 $DD$ と積 $\pi \backslash pi$ の反復的な再計算が必要です。対照的に、remove_liquidity() は比例して流動性を引き出し、反復計算を必要としません。

積をゼロから計算するための基本式は次のとおりです。

$$\begin{array}{cccc}& \pi =\prod _i{\left(\frac{D\cdot w_i}{x_i}\right)}^{n\cdot w_i}& & \text{(4)}\end{array}\backslash pi\; =\; \backslash prod\_\{i\}\; \backslash left(\backslash frac\{D\; \backslash cdot\; w\_i\}\{x\_i\}\backslash right)^\{n\; \backslash cdot\; w\_i\}\; \backslash tag\{4\}$$

ここで、$DD$ は供給、$w_{i}w\_i$ は資産 $ii$ の重み、$x_{i}x\_i$ はその仮想残高（コードでは vb[i] として保存）、$nn$ は資産数です。この形式は、セクション0x1.1の定義と代数的に同等であり、$D^{n}D^n$ が積に分配されています。

1. add_liquidity() には2つのパスがあります（セクション0x2.2でコードを表示）。

   • ブートストラップパス（prev_supply == 0 の場合）：式（4）を使用して、vb_prod をゼロから計算します。デプロイ後にこのパスがアクセス可能であることは、セクション0x2.2で議論されている状態管理の脆弱性です。
   • 通常パス（prev_supply > 0 の場合）：計算プロセスは2つのステップに分かれています。
     • a) 古い仮想残高と新しい仮想残高の比率に基づく増分更新を使用します。

       $$\begin{array}{cccc}& {\pi }_{\text{estimated}}=\pi \cdot \prod _{i=0}^{n-1}{\left(\frac{x_i}{x_i^{\mathrm{\prime }}}\right)}^{w_i\cdot n}& & \text{(5)}\end{array}\backslash pi\_\{\backslash text\{estimated\}\}\; =\; \backslash pi\; \backslash cdot\; \backslash prod\_\{i=0\}^\{n-1\}\; \backslash left(\backslash frac\{x\_i\}\{x\_i\text{'}\}\backslash right)^\{w\_i\; \backslash cdot\; n\}\; \backslash tag\{5\}$$

       ここで、$x_{i}x\_i$ と $x_i^{\mathrm{\prime }}x\_i\text{'}$ は預け入れ前後の仮想残高です。
     • b) この推定値を入力として _calc_supply() を呼び出し、インバリアント $DD$ と正確な $\pi \backslash pi$ の値を再計算することで、正確な値を反復的に校正します。

2. update_rates() は、交換レートが変更され、対応する資産の仮想残高が更新されるときにトリガーされます。その後の計算フローは、add_liquidity() の通常パスに従います。つまり、インバリアントは反復的に再計算されます。さらに、新しく計算された供給に基づいて、コントラクトはyETHをミントまたはバーンして、流動性供給が更新された仮想残高状態と一致することを保証します。

3. remove_liquidity() は、各仮想残高を比例的に削減した後、常に式（4）を使用してゼロから vb_prod を計算します。

0x2 根本原因分析

2つの脆弱性が悪用され、異なる役割と影響がありました。主な根本原因は、_calc_supply() インバリアントソルバーの計算上の欠陥であり、2つの障害モードがありました。（A）切り捨て丸めは積項をゼロにすることができ、インバリアントを定数和モデルに縮退させ、過剰なLPミント（供給インフレ）につながりました。そして（B）アンダーフロー条件も供給をインフレさせることができました。障害モードAのみがフェーズ2（〜810万ドル）で使用されました。障害モードBは、二次的な脆弱性と相互依存していました。

二次的な根本原因は、状態管理の欠陥でした。プールの初期化ブランチがアクセス可能なままでした。フェーズ2で供給がゼロにされた後、障害モードBとブートストラップパスが組み合わさって、追加で約90万ドルの損失（フェーズ3）を可能にしました。

0x2.1 `_calc_supply()` の不安全な算術演算（主）

図2は、_calc_supply() の実装をセクション0x1.2の数学的手順にマッピングし、以下で分析される2つの算術障害サイトを注釈付けしています。

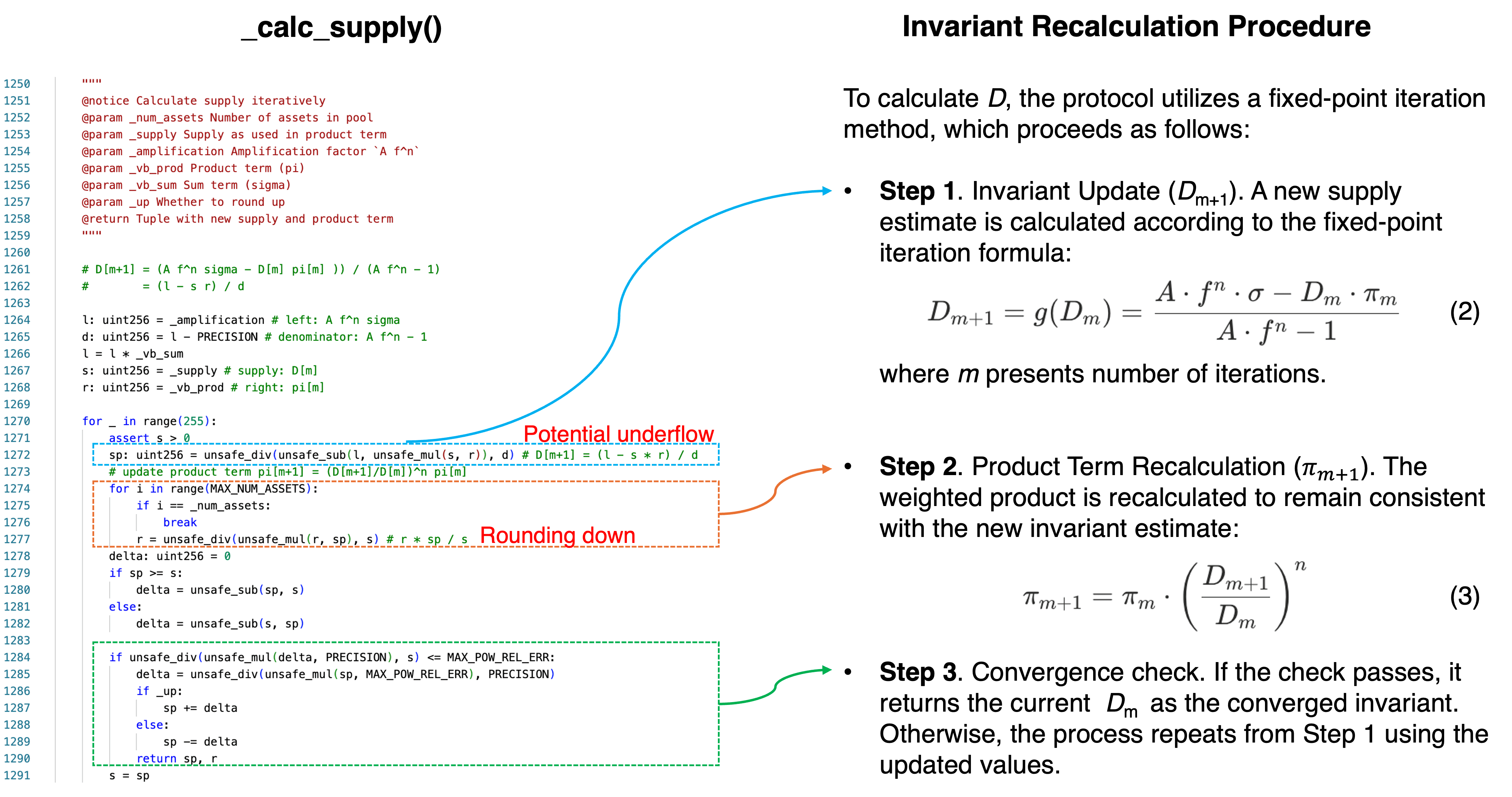
コード変数は次のように数学的用語にマッピングされます。

重要な式は次のとおりです。

sp = unsafe_div(unsafe_sub(l, unsafe_mul(s, r)), d)   # ステップ1: D[m+1]
r  = unsafe_div(unsafe_mul(r, sp), s)                 # ステップ2: π 更新 (資産ごと)

2つの算術障害モードがあり、それぞれ異なる行をターゲットにし、異なる効果を生み出します。どちらも、プールが極端な状態にあることをトリガーする必要があります。

通常の条件下では、反復は正しく動作します。l - s*r はわずかな正の値であり、反復は数回の反復で収束します。

1. 障害モードA：切り捨て丸めにより積がゼロになる

ステップ2では、積は資産ごとに次のように更新されます。

r = unsafe_div(unsafe_mul(r, sp), s)   # r = r * sp / s

unsafe_div() は整数除算を実行するため、常に切り捨て丸めを行います。プールが大幅に不均衡で、sp が s よりはるかに小さい場合（操作された大規模な預け入れ後に発生）、分子 r * sp は分母 s より小さくなる可能性があります。整数除算により、r = 0 となります。

r がゼロになると、後続のすべての反復でゼロのままになります。積項 $\pi \backslash pi$ は永久に崩壊しました。

一般的な誤謬は、この障害が pow_up() と pow_down() の間の丸め不一致から生じると主張しています。セクション0x4では、これが誤りである証拠を提示します。

2. 障害モードB：アンダーフローにより供給がインフレする

ステップ1では、新しい供給推定値は次のように計算されます。

sp = unsafe_div(unsafe_sub(l, unsafe_mul(s, r)), d)   # sp = (l - s*r) / d

l - s*r の減算 ${Af}^n\cdot \sigma -D_m\cdot {\pi }_m\backslash mathit\{Af\}^\{\backslash ,n\}\; \backslash cdot\; \backslash sigma\; -\; D\_m\; \backslash cdot\; \backslash pi\_m$ は式2にあります。通常の条件下では、これは正です。しかし、プールがゼロ供給の縮退状態に達すると、add_liquidity() の初期化ブランチ（セクション0x2.2で詳細）は式（4）（セクション0x1.3）を使用して積項をゼロから再計算し、相対的な magnitudes が反転する可能性があります。

具体的には、ダスト量のゼロ供給プールで add_liquidity() が呼び出されると、初期化ブランチは _calc_vb_prod_sum() を呼び出して、式（4）（セクション0x1.3）を使用して新しい値を計算します。微量の預け入れでは、vb_sum はごくわずか（例：16）ですが、ゼロに近い残高で除算し、高べき乗で累乗すると、積が不均衡に大きな値（例：〜9.13e20）に増幅されます。 s * r が l を超えると、減算は負の数学的結果を生成します。

unsafe_sub() がチェックされていない uint256 演算で減算を実行するため、負の結果は巨大な正の整数（$2^{256}2^\{256\}$ に近い）にラップアラウンドします。このラップアラウンド値は、除算と後続の反復を通じて伝播し、法外に大きな供給推定値を生成し、プロトコルはそれを実際のyETHトークンとしてミントします。

一般的な主張は、このようなアンダーフローが特定の供給操作ステップの2回目の反復で発生すると述べています。セクション0x4は、この主張が誤りであることを示しています。供給をインフレさせる実際のアンダーフローは、攻撃のフェーズ3で、まったく異なるコンテキストで発生します。

3. これらの障害が攻撃を可能にする方法

これらの2つの障害モードは、異なる影響を及ぼす異なるフェーズで動作します。

• 障害モードA（フェーズ2、〜810万ドル）：攻撃者が極端に不均衡なプールに預け入れると、積項がゼロになり、_calc_supply() がインフレした供給を返す原因となります。プロトコルは過剰にyETHを攻撃者にミントします。この障害モード単独で、ブートストラップパスの関与なしに、攻撃者がyETH Weighted StableSwap PoolからLST資産を空にすることができました。
• 障害モードB（フェーズ3、〜90万ドル）：供給がゼロにされた後、ブートストラップパスはダスト預け入れで大きな積項を再計算し、減算がアンダーフローを引き起こします。プロトコルは天文学的に大きな量のyETHをミントし、攻撃者はそれを使用して別のyETH/WETH Curve Poolを空にします。

依存関係は一方向です。障害モードAは単独で悪用可能であり、損失の90％の原因となりました。障害モードBは、フェーズ2がまず供給をゼロに駆動することを必要とします。

0x2.2 無効化されていないブートストラップパス（二次）

add_liquidity() 関数には、プールの初期預け入れのためのブランチが含まれています。

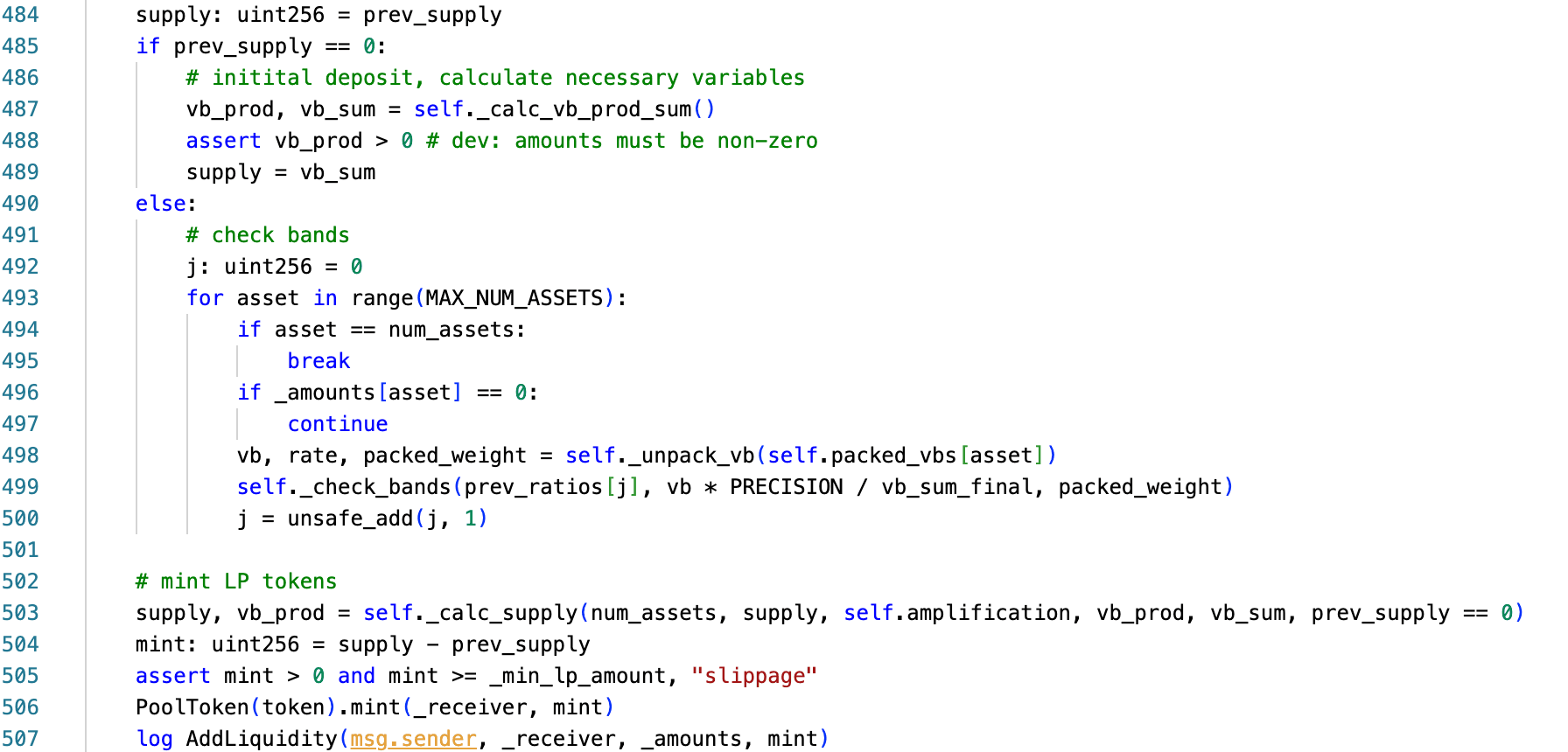
ロジックは次のように抽象化できます。

if prev_supply == 0:
    # ブートストラップパス — vb_prod と vb_sum をゼロから計算
    vb_prod, vb_sum = _calc_vb_prod_sum(balances, rates, weights, ...)
    supply = vb_sum
else:
    # 通常パス — 格納された vb_prod を使用し、増分チェックを実行
    ...

# 両方のブランチの後、prev_supply == 0 をフラグとして呼び出される
supply, vb_prod = _calc_supply(num_assets, supply, amplification, vb_prod, vb_sum, prev_supply == 0)

prev_supply == 0 の場合、関数は格納された状態をバイパスし、_calc_vb_prod_sum() を介して vb_prod と vb_sum をゼロから再計算し、それらを _calc_supply() に渡します。これは、プール初期化中に一度だけ使用されることを意図していましたが、最初の預け入れ後に永続的にゲートされませんでした。

総供給がゼロに駆動される場合（バーンと引き出しの任意の組み合わせによる）、ブランチが再び到達可能になります。このパスに再エントリする攻撃者は、通常のプール操作では発生しないパラメータで算術障害をトリガーする可能性があります。

これは既知の脆弱性パターンです。2023年8月、Balancer V2インシデントも、攻撃者が有利なパラメータで初期化ロジックに再エントリできるように、供給をゼロに駆動することに依存していました[6]。デプロイされたプールを初期状態に戻すことができるか、またその際にどのようなインバリアントが成り立つかは、プロトコル設計者が明示的に対処する必要がある問題です。

0x3 攻撃分析

エクスプロイトは、攻撃トランザクション[5]の調整されたシーケンス全体で3つのフェーズに展開されます。各フェーズは、前のフェーズによって確立された状態に基づいています。

0x3.1 フェーズ1：プールを歪める（準備）

目標： 資産間の仮想残高に極端な不均衡を作成する。

以下の図は、このフェーズのトランザクショントレースを示しています（フラッシュローンステップはスペースの都合上省略されています）。

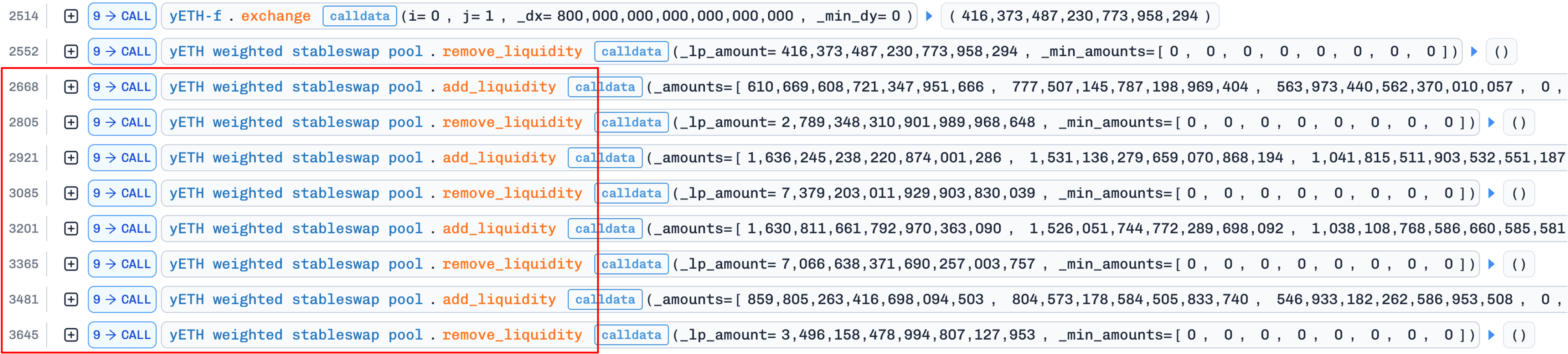
攻撃者はまず、BalancerとAaveからフラッシュローンを介して大量のLST資産（具体的には5,500e18 wstETH、3,100e18 WETH、1,800e18 rETH、2,000e18 ETHx、および200e18 cbETH）を借入しました。

次に、攻撃者はyETH/WETH Curve Poolで約800e18 WETHを約416e18 yETHにスワップし、取得したyETHを使用してプールから流動性を引き出しました。

主な操作は、セクション0x1（背景）で説明されているインターフェースの非対称性を利用します。add_liquidity() は任意の比率の預け入れを許可しますが、remove_liquidity() はプール重みに比例して資産を引き出します（上記の図の赤い四角で強調されています）。追加 → 削除のサイクルを繰り返し、少数の選択された資産のみを預け入れ、すべての資産を比例して引き出すことにより、攻撃者はプールを極端に不均衡な状態に徐々に駆動します。

資産3（cbETH）、6（WOETH）、および7（mETH）は98％以上枯渇しました。この不均衡は直接利益を抽出しません。次のフェーズの数値的な事前条件を作成します。

0x3.2 フェーズ2：供給をゼロに崩壊させる（〜810万ドル）

目標： インバリアント積をゼロに駆動し、その後yETH供給をゼロに排出する。このフェーズは、主脆弱性（不安全な算術演算）のみを悪用し、総損失の約90％の原因となりました。

このフェーズでは、3回実行される5ステップの繰り返しサイクルを使用します。

1. add_liquidity() により積を破損する。
2. add_liquidity() により修正のための事前条件を確立する。
3. 0 yETH で remove_liquidity() により積をリセットする。
4. update_rates() により供給を修正する。
5. remove_liquidity() により資産を引き出す。

以下の図は、5ステップサイクルの3回の繰り返しが明確に見えるトランザクショントレースを示しています。

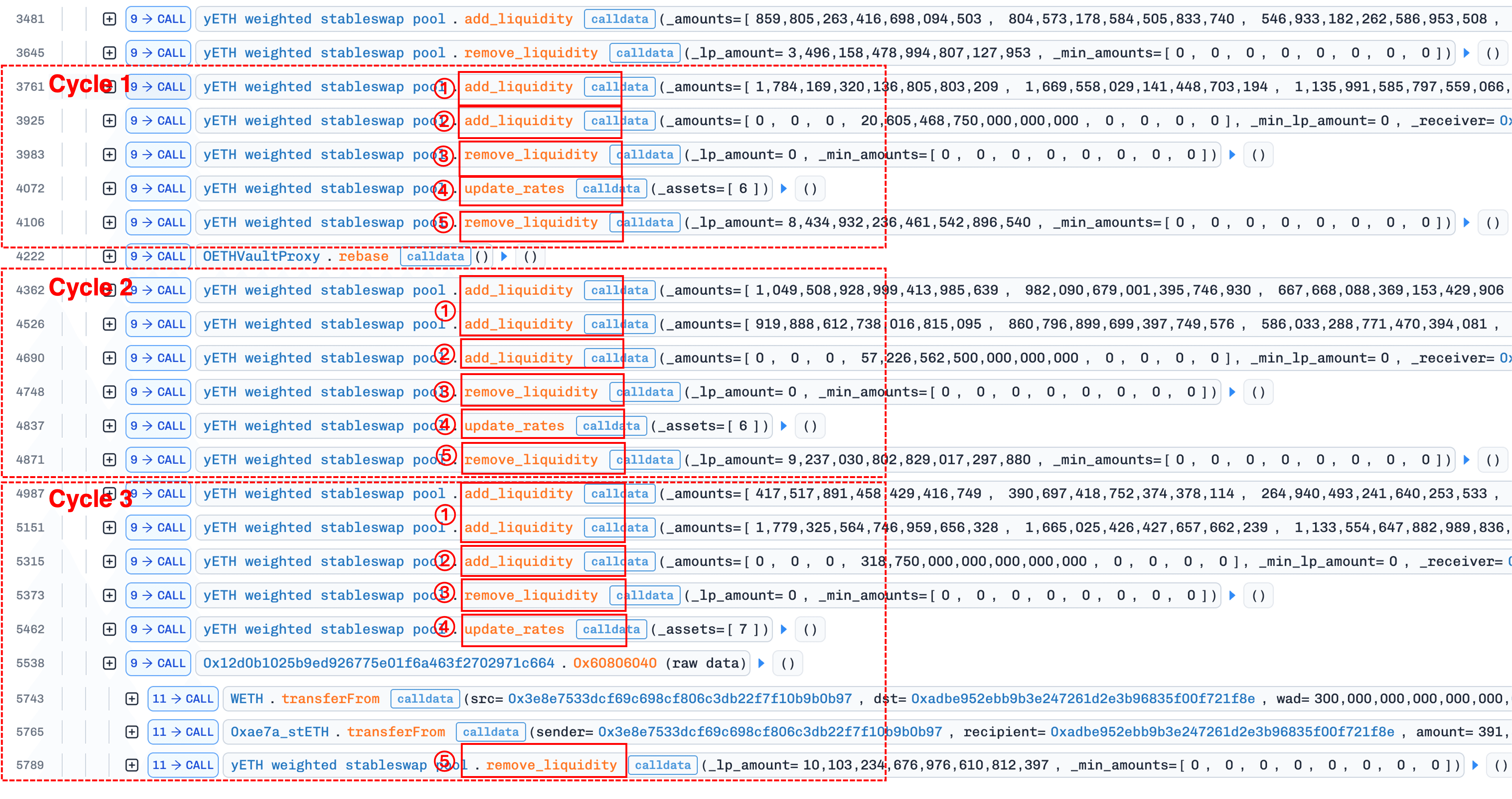
1. `add_liquidity()` により積を破損する

攻撃者は、高重み資産（インデックス0、1、2、4、5：sfrxETH、wstETH、ETHx、rETH、apxETH）の大部分を預け入れます。各資産の預け入れ量は、現在の仮想残高の約3倍です。

add_liquidity() は、式（5）（セクション0x1.3）の増分更新により、新しい積項を推定します。$x_i^{\mathrm{\prime }}\gg x_{i}x\_i\text{'}\; \backslash gg\; x\_i$ は高重み資産に対してすべて当てはまるため、比率 $(x_i\mathrm{/}{x}_i^{\mathrm{\prime }})(x\_i\; /\; x\_i\text{'})$ はすべて1未満の小数であり、高べき乗で累乗されます。これにより、${\pi }_{\text{new}}\backslash pi\_\{\backslash text\{new\}\}$ は〜42e18から〜0.00353e18に縮小し、ほぼゼロの推定積となります。

この微小な積が _calc_supply() に入ります。反復では、積の更新 r = r * sp / s は、セクション0x2（根本原因分析）で説明されている切り捨て丸め条件に遭遇します。分子は分母より小さくなり、整数除算により r はゼロに切り捨てられます。関数はゼロ積を返し、インフレした供給（〜vb_sum）を返すため、プロトコルはyETHを過剰にミントします。

2. `add_liquidity()` により修正のための事前条件を確立する

攻撃者は、資産インデックス3（cbETH、枯渇した低重み資産）の単一サイド流動性を追加し、約6.5倍の資産の現在のプール残高を預け入れます。これはわずかなyETHトークンしか受け取りませんが、プールを再バランスさせ、次の反復が激しく振動しないようにします。

このステップがない場合、ステップ3で積をゼロ以外にリセットした後でも、フェーズ4の反復は極端な不均衡から激しい振動が発生するため、ゼロ積になります。当社のFoundryシミュレーションはこれを保証します。ステップ2をスキップすると、ステップ4での修正が失敗します。

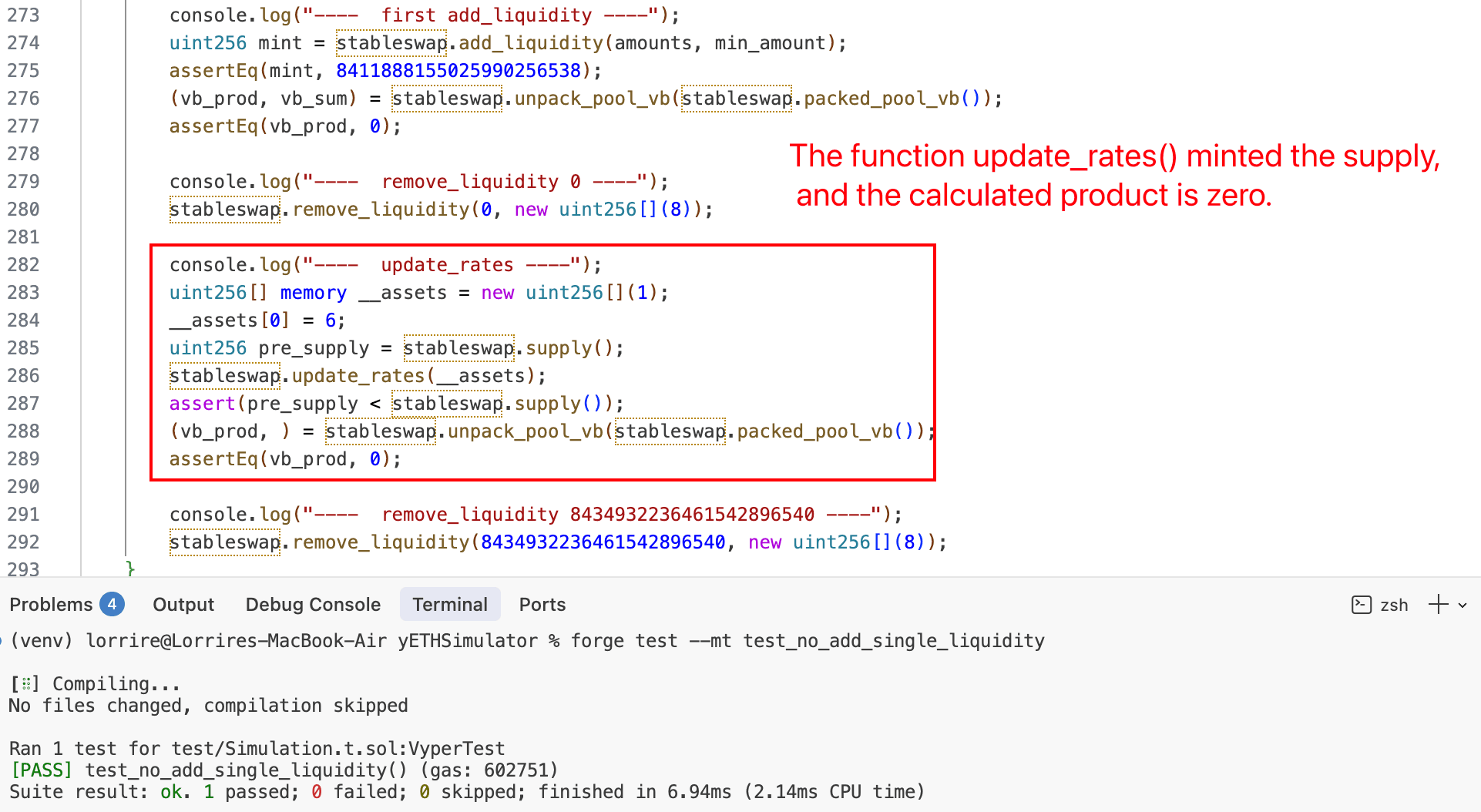
3. 0 yETH で `remove_liquidity()` により積をリセットする

攻撃者は remove_liquidity() を0の額で呼び出します。トークンは引き出されませんが、関数は現在のプール状態から式（4）（セクション0x1.3）を使用して**vb_prod を再計算します**。仮想残高がゼロ以外であるため、これはゼロ以外の積（〜9.09e19）を生成し、破損したゼロ値を上書きします。

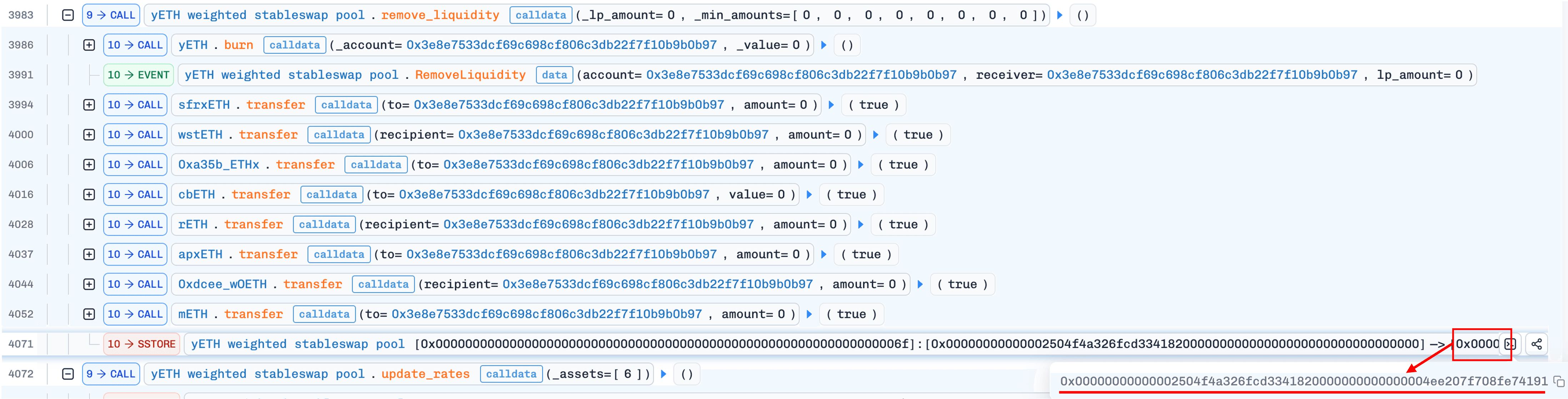
4. `update_rates()` により供給を修正する

攻撃者は資産インデックス6（WOETH）または7（mETH）に対して update_rates() を呼び出します。交換レートが最後に更新されてから変更されている場合、関数は、復元された（ゼロ以外の）積を持つ _calc_supply() をトリガーします。今回は、反復が正しく収束し、現在のインフレした値よりもはるかに低い供給値を生成します。差額はyETHステーキングコントラクトからバーンされます。公式の事後分析[2]によると、これはProtocol-Owned Liquidity（POL）を構成します。つまり、バーンは攻撃者の保有ではなく、プロトコルのポジションを削減します。この非対称性は重要です。各サイクルは、攻撃者のyETH残高がそのまま維持されながら、総供給を削減します。

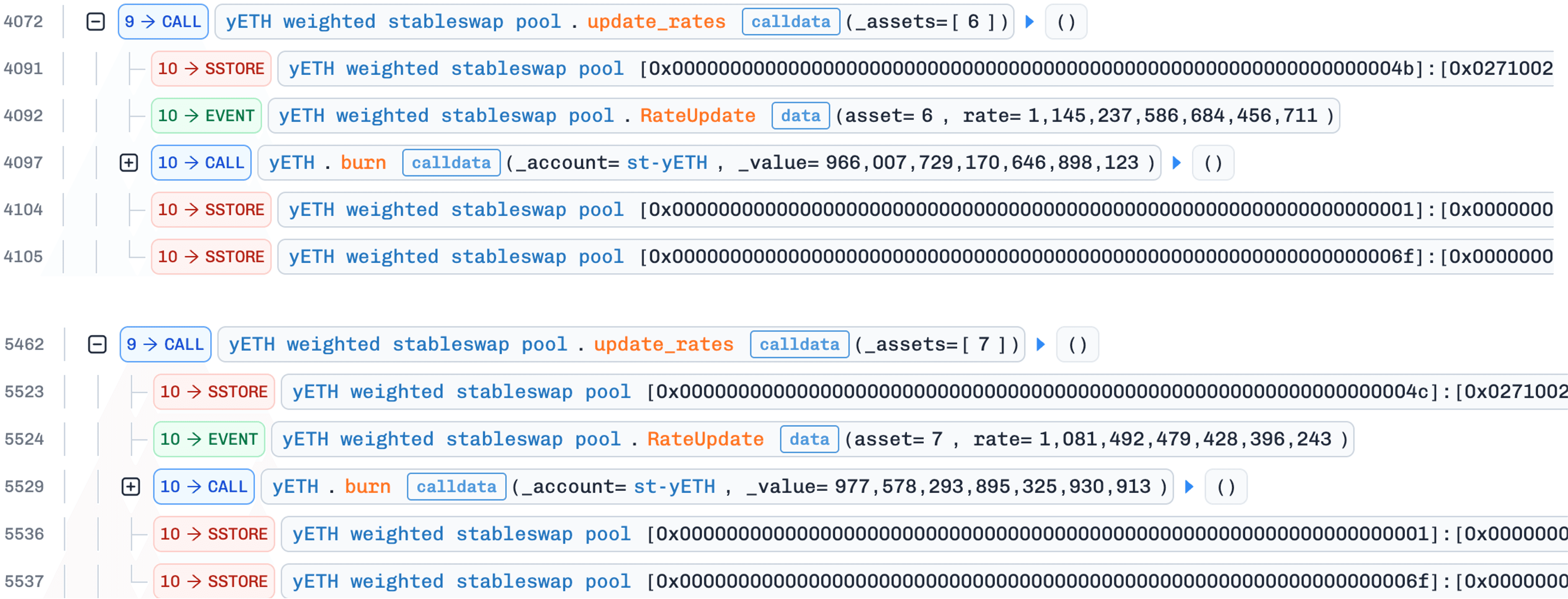
レートの不一致自体は利益の源ではありません。それは純粋にトリガーメカニズムとして機能します。3つのプールインターフェースのうち、add_liquidity() と update_rates() だけが _calc_supply() を呼び出します。remove_liquidity() は比例スケーリングを使用し、呼び出しません。ステップ3でゼロ以外の積を復元した後、攻撃者は追加の資産を預け入れることなく _calc_supply() をトリガーする必要があります。不正確なレートで update_rates() を呼び出すことは、まさにこれを達成します。レートの変更は、攻撃者に追加コストなしで _calc_supply() の供給再計算をトリガーします。

これが攻撃の微妙な側面を説明しています。準備フェーズ（フェーズ1）中、攻撃者はWOETHとmETHへの流動性の追加を意図的に避けました。これらのレートが add_liquidity() 中に更新されていた場合、レートの不一致は存在せず、このステップでの update_rates() は _calc_supply() をトリガーしませんでした。

5. `remove_liquidity()` により資産を引き出す

各サイクルの終わりに、攻撃者は remove_liquidity() を介して引き出します。

利益抽出方法

利益メカニズムは次のようになります。ステップ1では、攻撃者はLSTを預け入れ、過剰にミントされたyETH（破損した積のため）を受け取ります。ステップ4で、供給が修正されると、過剰なyETHはPOL（ステーキングコントラクト）からバーンされ、攻撃者からではありません。ステップ5では、攻撃者はyETH保有量に比例してLSTを引き出します。POLがバーンを吸収する一方で、攻撃者のyETH残高はそのまま維持されたため、攻撃者は預け入れた量よりも多くのLSTを引き出すことになります。この差額は、3サイクルにわたって抽出され、合計で約810万ドルになります。

リベースの目的

トレース（最初のサイクルと2回目のサイクルの間）では、OETHVaultProxy.rebase() の呼び出しも示されています。これはOETHのリベースをトリガーします。WOETHコントラクトが保持するOETH残高が増加し、WOETHの実効交換レートが上昇します。この「保存された」レートの不一致は、2回目のサイクルのステップ4を再び可能にするものです。update_rates() が最終的に呼び出されると、不一致を検出し、_calc_supply() をトリガーします。

ゼロへの排出

この5ステップサイクルを3回繰り返した後、攻撃者はプールの総供給量を保有しているyETH量より少なくしました。最後の remove_liquidity() 呼び出しは、残りの供給量をゼロに排出します。

プールは現在、ゼロ供給、ゼロ積、ゼロ vb_sum を保持しています。この縮退状態は、以前の預け入れがあったプールが決して初期化されていない状態に戻らないという暗黙の設計仮定に違反しています。

0x3.3 フェーズ3：ゼロ供給を悪用した追加利益（〜90万ドル）

目標： 縮退したプール状態から巨大な量のyETHをミントし、その後、実資産にスワップする。このフェーズは、二次的な脆弱性（無効化されていないブートストラップパス）と障害モードB（アンダーフロー）の相互依存的な組み合わせを悪用し、合計で総損失の約10％を占めました。

1. アンダーフローによるミント

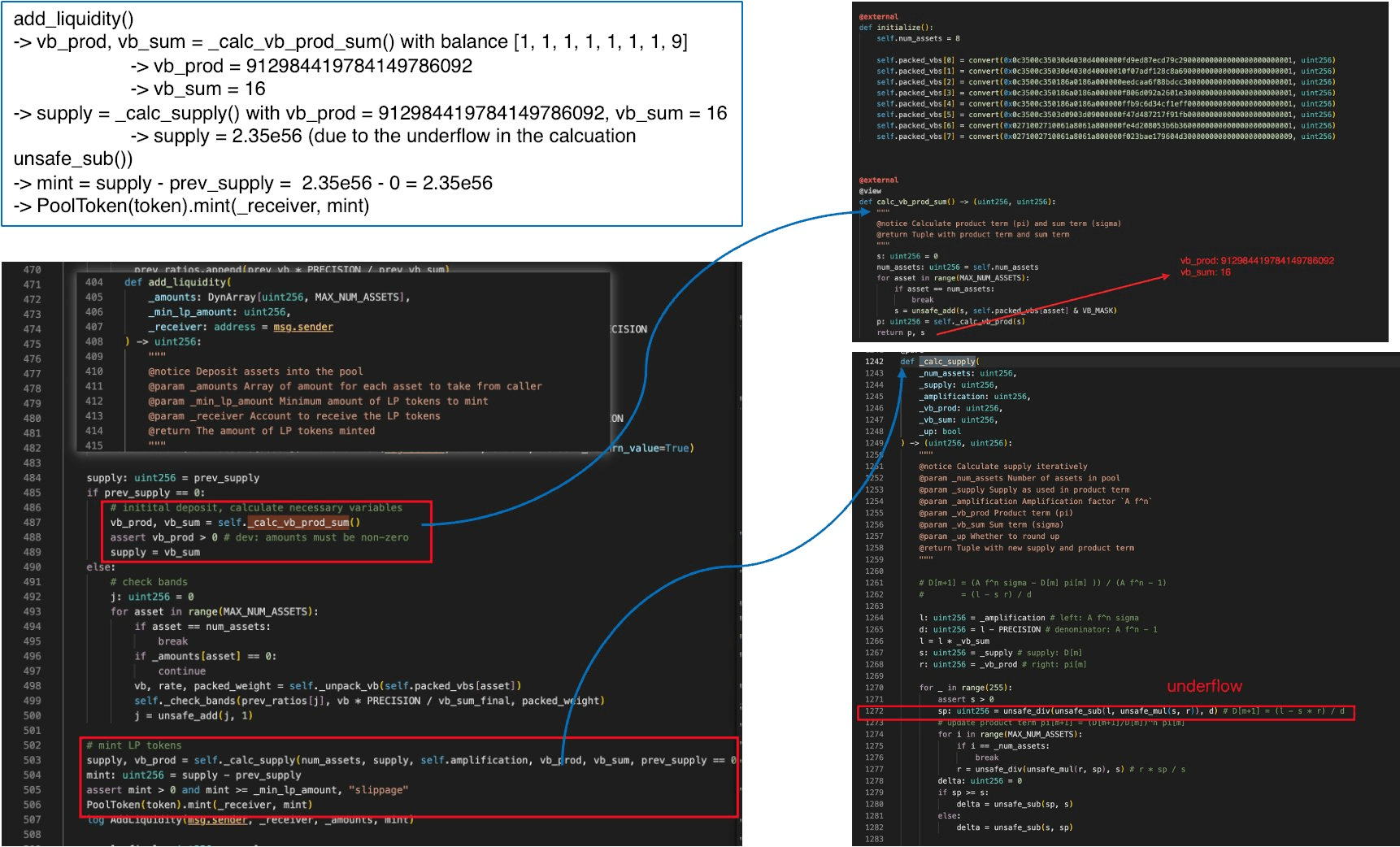
総供給がゼロになったため、攻撃者はダスト量の add_liquidity() を呼び出します（残高 [1, 1, 1, 1, 1, 1, 1, 9]）。

prev_supply == 0 であるため、コードはセクション0x2（根本原因分析）で説明されているブートストラップパスに入ります。格納された状態をバイパスし、_calc_vb_prod_sum() を介して vb_prod と vb_sum をゼロから再計算し、それらを _calc_supply() に渡します。これは2番目の脆弱性の稼働中です。攻撃者はプールを初期化されていない状態に戻し、ソルバーに渡される初期条件を制御しました。

すべての仮想残高がダストレベル（交換レートが1e18に近い）にあるため、計算された値は次のようになります。

• vb_sum = 16
• vb_prod ≈ 9.13e20
• _supply = vb_sum = 16

_calc_supply() 内で、変数は次のように初期化されます。

• l = _amplification * _vb_sum ≈ 4.5e20 × 16 ≈ 7.2e21
• d = _amplification - PRECISION ≈ 4.49e20
• s = _supply = 16
• r = _vb_prod ≈ 9.13e20

ここで減算 l - s * r を計算します。

$$7.2\times {10}^{21}-16\times 9.13\times {10}^{20}=7.2\times {10}^{21}-1.46\times {10}^{22}\approx -7.4\times {10}^{21}7.2\; \backslash times\; 10^\{21\}\; -\; 16\; \backslash times\; 9.13\; \backslash times\; 10^\{20\}\; =\; 7.2\; \backslash times\; 10^\{21\}\; -\; 1.46\; \backslash times\; 10^\{22\}\; \backslash approx\; -7.4\; \backslash times\; 10^\{21\}$$

これは負です。チェックされていない uint256 演算では、unsafe_sub はこれを約 $2^{256}-7.4\times {10}^{21}2^\{256\}\; -\; 7.4\; \backslash times\; 10^\{21\}$ にラップアラウンドします。これは法外に大きな値です。 d（〜4.49e20）で除算した後、結果の供給推定値は約 2.35e56 となり、プロトコルはこれらすべてを攻撃者にミントします。このアンダーフローは、フェーズ2で総供給がゼロに駆動されたためにのみ可能です。非縮退したプール状態では、l > s * r が成り立つため、減算は安全です。

2. 実資産へのスワップ

攻撃者は、過剰にミントされたyETHの一部をyETH–WETH Curve Poolで約1,097e18 WETHにスワップし、そのWETH準備金を空にします。フェーズ1で費やされた800e18 WETHを考慮すると、純利益は約90万ドルでした。

フェーズ2で抽出された約810万ドルのLST資産と合わせて、攻撃者は合計で約900万ドルの利益を得ました。

詳細な資金フロー分析（資金源と宛先アドレスを含む）は、他の公開されている分析（例：[2]）でカバーされており、この記事の範囲外です。

0x4 誤解の修正

このインシデントのほとんどの公開された分析は、攻撃者が事前条件をどのように設定したかを完全に説明せずに、算術的な症状に焦点を当てています。2つの特定の主張は修正に値します。

0x4.1 主張：「`pow_up()` と `pow_down()` の間の丸め不一致がインバリアントを破損する」

一般的な解釈では、pow_up() と pow_down() の使用方向の不一致が、悪用可能な不整合をもたらすと主張して、根本原因を pow_up() と pow_down() の方向性の違いに帰しています。

これを直接テストしました。コントラクトを修正して、一貫して pow_down() を使用するように（すべての pow_up() 呼び出しを置き換える）し、Foundryで完全な攻撃シミュレーションを再実行しました。エクスプロイトは同様に成功しました。 積は依然としてゼロに崩壊し、供給は排出され、アンダーフローは依然としてインフレしたミントを生成しました。

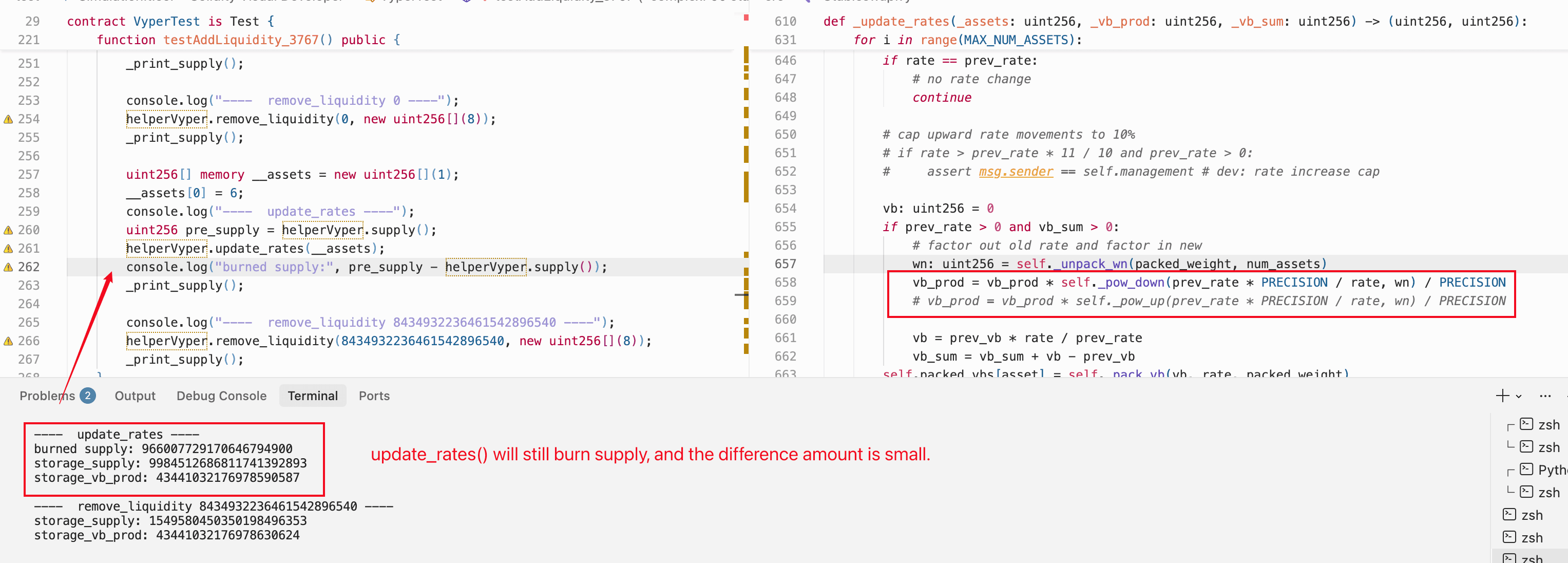
ゼロ積状態を可能にする丸めは、pow() 関数での丸め方向ではなく、反復ループ内の r = unsafe_div(unsafe_mul(r, sp), s) における床除算です。

0x4.2 主張：「2回目の反復でのアンダーフローが中間項をゼロにする」

広く引用されている説明は、_calc_supply() の2回目の反復中に、unsafe_sub のアンダーフローが sp ≈ 1.94e18 を生成し、それが r をゼロに丸める原因となると述べています。

Foundry（オンチェーンリプレイ）とPython（数学的検証）の両方を使用して、正確な中間値を再現しました。Foundryシミュレーションは、_calc_supply() を反復ごとにトレースします。

======= _calc_supply iteration 0 =======
  l = 4905875511098192451202650000000000000000
  s = 2514373972590845290489        ← 初期供給
  r = 3538247433646816               ← 初期積 (非常に小さい)
  d = 4490000000000000000000

  sp = (l - s*r) / d ≈ 1.093e22     ← 新しい供給が約4倍にジャンプ
  new r ≈ 4.49e22                    ← 積が劇的にインフレ

======= _calc_supply iteration 1 =======
  s = 10926206313726454855296        ← 前の sp から
  r = 44892226765713223838396        ← 前の内部ループから

  sp = 19113493328251743069          ← ≈ 1.91e19、正当に小さい
  new r = 0                          ← ゼロに丸められる！

重要な観察：反復1では、sp は約1.91e19と評価されます。これは正当に小さな正の値であり、アンダーフローのアーティファクトではありません。増幅重み付き合計 l と供給積項 s*r がこの反復で近い大きさであるため、減算 l - s*r はわずかな正の結果を生成します。

積をゼロにするのは、その後に起こることです。内部ループは r = r * sp / s を計算します。ここで sp（〜1.91e19）は s（〜1.09e22）よりもはるかに小さいです。分子 r * sp は分母 s より小さくなり、整数除算により結果はゼロに丸められます。

Pythonで同じ値を任意精度整数で計算し、減算がアンダーフローしないことを確認して、これを独立に検証しました。

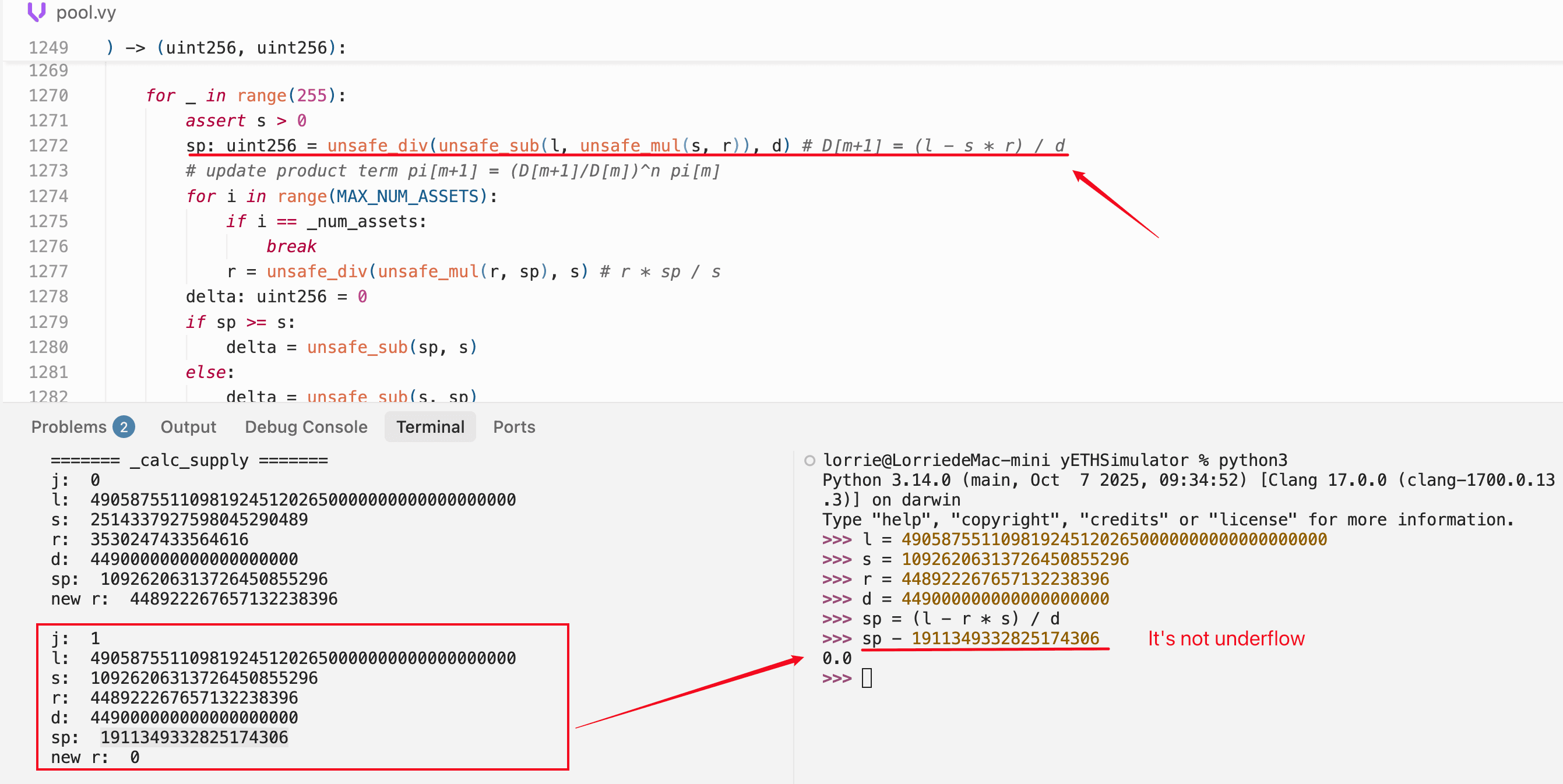
積は、減算のアンダーフローではなく、除算の丸めによってゼロになります。供給をインフレさせる unsafe_sub アンダーフローは、まったく異なるコンテキストで発生します。フェーズ3の攻撃で、ゼロ供給に排出されたプールにダスト流動性が追加される場合です。

0x5 結論

yETHエクスプロイトは、非対称な影響を持つ2つの脆弱性を伴いました。不安全な算術演算は _calc_supply() にあり、主要な根本原因でした。その切り捨て丸め障害（障害モードA）は、フェーズ2だけで〜810万ドルの損失を独立に可能にしました。無効化されていないブートストラップパスは二次的な脆弱性でした。障害モードB（アンダーフロー）と組み合わされて、〜90万ドルの追加利益（フェーズ3）を可能にしましたが、フェーズ2がすでに供給をゼロに排出した後でした。この損失の内訳は、フェーズ2とフェーズ3の利益を区別しない他の公開レポートから、本分析を区別します。

公式の事後分析[2]は5つの根本原因を特定しています。これらを2つの欠陥（公式の#1と#5を統合した不安全な算術演算。無効化されていないブートストラップパスを#4として）と2つのアーキテクチャ上の事前条件（#2 非対称なΠ処理。#3 POLによるゼロ供給状態）に再分類します。区別：欠陥は設計意図に違反する実装バグです（ソルバーはゼロ積を生成したりアンダーフローしたりすべきではない）。一方、事前条件は設計上の選択であり、欠陥と組み合わされたときに悪用可能な攻撃サーフェスを作成する場合、意図どおりに機能します。

推奨事項

• インバリアントソルバーでのチェック付き算術演算。 ガス効率を犠牲にしてでも、アンダーフロー/オーバーフロー時の明示的なリバートを伴うsafe_divとsafe_subを使用してください。ソルバーは最大256回の反復で実行され、ガスオーバーヘッドはセキュリティリスクと比較して無視できます。
• 中間値の境界チェック。 積項が反復間で健全な範囲内に留まることを検証します。積がゼロに低下したり、反復間で供給推定値が桁違いに増加したりすることは、縮退状態を示します。
• 不均衡制限。 資産の仮想残高と、そのターゲットの重み比例残高との間の最大偏差を強制します。これにより、フェーズ1が事前条件を作成することを防ぐことができます。
• インバリアント単調性チェック。 _calc_supply() が返された後、新しい供給が変化の方向と一致していることを検証します（流動性の追加は供給を減らすべきではなく、レート更新は10倍の変化を生成すべきではないなど）。
• 初期化パスの永続的な無効化。 プールの最初の預け入れ後、prev_supply == 0 ブートストラップブランチをゲートして、再エントリできないようにします。これにより、フェーズ3が完全にブロックされます。
• ゼロ供給状態の防止。 プールがゼロ以外の残高を保持している間、プロトコルレベルのバーン（POLまたはステーキングコントラクトから）が総供給をゼロに削減できないことを保証します。最小供給フロアは、ブートストラップ再エントリを可能にする縮退状態への遷移をブロックします。
• リアルタイム異常検出。 異常な状態遷移（積項がゼロに低下する、供給が桁違いに変化する、短期間に繰り返しの追加/削除サイクルが発生するなど）を監視し、損失が累積する前にアラートまたはサーキットブレーカーをトリガーします。

参考文献

1. Yearn Finance インシデント発表
2. Yearn Security 事後分析
3. yETH ドキュメント
4. yETH ホワイトペーパー: インバリアント導出
5. BlockSec Explorer の攻撃トランザクション
6. BlockSec: Balancer ブーストプールインシデントの分析（2023年8月）

BlockSecについて

BlockSecは、フルスタックのブロックチェーンセキュリティおよび暗号コンプライアンスプロバイダーです。私たちは、プロトコルおよびプラットフォームのライフサイクル全体を通じて、コード監査（スマートコントラクト、ブロックチェーン、ウォレットを含む）、リアルタイムでの攻撃傍受、インシデント分析、不正資金追跡、AML/CFT義務の遵守を支援する製品とサービスを構築しています。

BlockSecは、著名な会議で複数のブロックチェーンセキュリティ論文を発表し、DeFiアプリケーションのいくつかのゼロデイ攻撃を報告し、複数のハッキングをブロックして2000万ドル以上を救済し、数十億ドル相当の暗号資産を確保してきました。

• 公式ウェブサイト：https://blocksec.com/
• 公式Twitterアカウント：https://twitter.com/BlockSecTeam
• 🔗 BlockSec 監査サービス : リクエストを送信
• 🔗 Phalcon Security APP : デモを予約
• 🔗 Phalcon Compliance