#10 パノプティック事件：XOR線形性が位置フィンガープリントスキームを破る

2025年8月25日、CantinaとSeal911の協力を得て、Panopticはホワイトハットレスキュー作戦を実行し、約40万ドルのリスク資産を確保しました [1]。根本原因は s_positionsHash の構築における欠陥でした。プロトコルは、ポジションIDのKeccak256ハッシュをXORで集約して単一のフィンガープリントを作成していました。個々のKeccak256ハッシュは衝突耐性を維持しますが、XORの数学的線形性により、複合フィンガープリントは安全ではありませんでした。攻撃者は、XOR集約ハッシュが任意のターゲットフィンガープリントと一致する偽のポジションIDのセットを生成し、プロトコルのポジション検証をバイパスして、負債を返済せずに担保を引き出すことができました。

背景

Panopticは、ユーザーがプットオプションとコールオプションを取引できる、イーサリアム上に構築された分散型永久オプション取引プロトコルです。

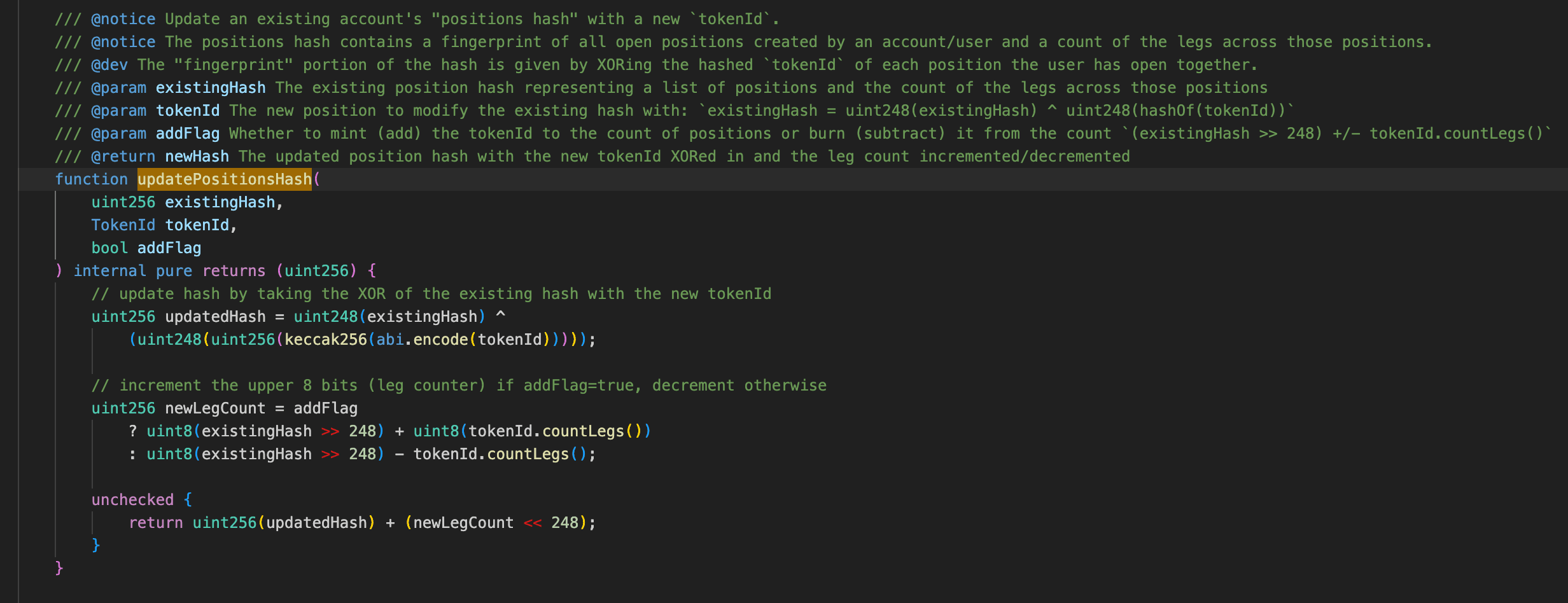
withdraw() 関数には、tokenId のセットで構成される入力パラメータ positionList があります。各 tokenId はポジションを表します。 withdraw() 関数は、s_positionsHash に基づいて各ポジションの負債状況をチェックし、その後ユーザーの担保を取得します。

ガスを節約するため、プロトコルはユーザーのすべてのポジション (tokenId) を保存しません。代わりに、ユーザーのすべての tokenId に基づいてフィンガープリントを計算し、s_positionsHash に記録します。各 s_positionsHash の最上位8ビットは numLegs を表し、下位248ビットは user position hash を表します。

渡された各 tokenId について、プロトコルはそのハッシュを計算し、下位248ビットを取得し、現在の s_positionsHash の下位248ビットとのビットごとのXORを実行して user position hash を更新します。

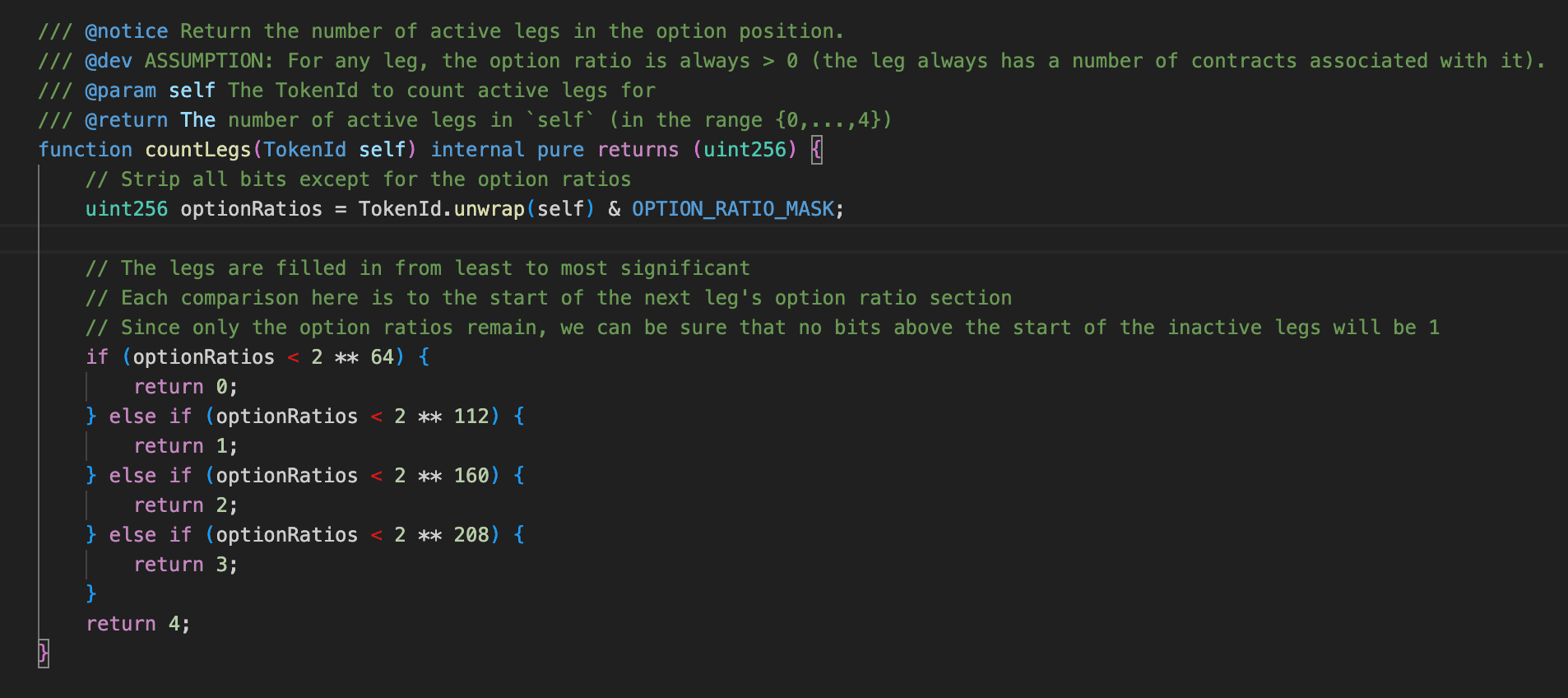
同時に、countLegs は tokenId の数値範囲に基づいて調整されます。 tokenId が $2^{64}2^\{64\}$ 未満の場合は変更されず、範囲 $(2^{64},2^{112})(2^\{64\},\; 2^\{112\})$、$(2^{112},2^{168})(2^\{112\},\; 2^\{168\})$、および $(2^{168},2^{208})(2^\{168\},\; 2^\{208\})$ の場合はそれぞれ1、2、または3増加します。これは最終的に s_positionsHash の上位8ビットに書き込まれて numLegs が更新されます。

脆弱性分析

根本原因は、s_positionsHash を構築するコントラクトのアルゴリズム、特にKeccak256ハッシュ結果を集約するためにXOR演算を使用することにおける欠陥でした。単一のハッシュ関数は安全ですが、XOR演算の数学的線形性により、全体的なフィンガープリントアルゴリズム（つまり、ハッシュのXOR合計）は安全ではありません [2]。

線形性とは、攻撃者がハッシュ関数自体を破る（つまり、ハッシュから tokenId を逆算する）必要がないことを意味します。代わりに、組み合わせ戦略を採用できます。多数のランダムな tokenId を生成し、それらの Keccak256(tokenId) を計算し、これらのハッシュ値から、これらの tokenId ハッシュのXOR合計が正確に犠牲者のターゲットフィンガープリントと一致するような特定のサブセットを選択します。

これにより、攻撃者は withdraw() を呼び出す際に偽の tokenId のセットを渡すことができ、ヘルスチェックを通過し、s_positionsHash に対応するすべての担保を取得できます。

理論

ユーザーのポジションフィンガープリント s_positionsHash が user position hash $TT$ と numLegs $kk$ を持ち、ユーザーの tokenId を $\{t_1,t_2,\dots ,t_n\}\backslash \{t\_1,\; t\_2,\; \backslash dots,\; t\_n\backslash \}$ と仮定します。したがって：

$$\underset{i=1}{\overset{k}{⨁}}[\text{Hash}(t_i)(\mathrm{m}\mathrm{o}\mathrm{d}{2}^{248})]=T\backslash bigoplus\_\{i=1\}^\{k\}\; [\backslash text\{Hash\}(t\_i)\; \backslash pmod\{2^\{248\}\}]\; =\; T$$

ここで、各248ビットハッシュ値は248次元ベクトルと見なすことができます。

$$\text{Hash}(t_i)(\mathrm{m}\mathrm{o}\mathrm{d}{2}^{248})=[b_0,b_1,\dots ,b_{247}{]}^T,\text{ここで }{b}_i\in \{0,1\}\backslash text\{Hash\}(t\_i)\; \backslash pmod\{2^\{248\}\}\; =\; [b\_0,\; b\_1,\; \backslash dots,\; b\_\{247\}]^T,\; ここで\backslash \; b\_i\; \backslash in\; \backslash \{0,\; 1\backslash \}$$

したがって、$TT$ は0と1で構成される248次元空間 (${\mathbb{F}}_2^{248}\backslash mathbb\{F\}\_2^\{248\}$) に存在します。この空間では、XOR演算はベクトル加算に相当します（付録I）。

攻撃者の目標は、それらのXOR合計の下位248ビットが $TT$ と等しくなるような、利用可能なすべてのベクトルから $nn$ 個の248次元ベクトル $\{v_1,v_2,\dots ,v_n\}\backslash \{v\_1,\; v\_2,\; \backslash dots,\; v\_n\backslash \}$ を見つけることです。したがって、攻撃者の目的を線形方程式のシステムとして定式化できます。

$$x_1{v}_1+x_2{v}_2+\cdots +x_n{v}_n=Tx\_1\; v\_1\; +\; x\_2\; v\_2\; +\; \backslash dots\; +\; x\_n\; v\_n\; =\; T$$

具体的には、$TT$ を直接構築しようとする必要はありません。代わりに、$nn$ 個の線形独立なハッシュベクトル $\{v_1,v_2,\dots ,v_n\}\backslash \{v\_1,\; v\_2,\; \backslash dots,\; v\_n\backslash \}$ （ここで $nn$ は次元248に等しい）を選択し、それらを列ベクトルとして使用して $n\times nn\; \backslash times\; n$ 行列 $AA$ を構築します。

$$A=[v_1,v_2,\dots ,v_n]A\; =\; [v\_1,\; v\_2,\; \backslash dots,\; v\_n]$$

問題は、次のような係数ベクトル $xx$ を見つけることに変換されます。

$$A\cdot x=TA\; \backslash cdot\; x\; =\; T$$

ここで、$x=[x_1,x_2,\dots ,x_n{]}^{T}x\; =\; [x\_1,\; x\_2,\; \backslash dots,\; x\_n]^T$ であり、$x_i\in \{0,1\}x\_i\; \backslash in\; \backslash \{0,\; 1\backslash \}$ です。

線形代数の理論によれば、行列 $AA$ がフルランクである限り、それは $nn$ 次元の空間全体をスパンします。これは、任意のターゲット $TT$ に対して、方程式のシステムが一意の解を持つことを意味します。$xx$ を解いた後、$x_i=1x\_i=1$ となるベクトル $v_{i}v\_i$ を保持するだけでよく、それらのXOR合計は $TT$ になります。

例

理解を容易にするために、ケーススタディでこの構築プロセスを説明します。ベクトルが3次元で、各次元が0または1のみで構成され、ターゲットハッシュ値が 101、つまり $T=[1,0,1{]}^{T}T\; =\; [1,\; 0,\; 1]^T$ であると仮定します。

次に、3つのハッシュ値をランダムに生成します。

• $v_1=[1,1,0{]}^{T}v\_1\; =\; [1,\; 1,\; 0]^T$
• $v_2=[0,1,0{]}^{T}v\_2\; =\; [0,\; 1,\; 0]^T$
• $v_3=[0,1,1{]}^{T}v\_3\; =\; [0,\; 1,\; 1]^T$

これらの3つのベクトルを列として使用して行列 $AA$ を構築し、方程式 $Ax=TAx=T$ を設定します。

ガウスの消去法で解くと、$x=[1,0,1{]}^{T}x\; =\; [1,\; 0,\; 1]^T$ が得られます。これは、$v_{1}v\_1$ と $v_{3}v\_3$ （$x_1=1,x_3=1x\_1=1,\; x\_3=1$ に対応）を選択する必要があることを意味し、それらのXOR合計は正確にターゲット $TT$ に等しくなります。

$n$ 個の線形独立なベクトルの選択

前述のように、$Ax=TAx=T$ を解くには、フルランク行列 $AA$ を構築する必要があります。非常に大きなベクトル空間 ($m=2^{248}m\; =\; 2^\{248\}$) を扱っているため、中心的な質問は次のようになります。この広大な空間から $nn$ 個の線形独立なベクトルを迅速に選択するにはどうすればよいでしょうか？

最も簡単な方法を考えます。$nn$ 個の tokenId をランダムに生成し、それらのハッシュ結果をベクトルとして選択します。

${\mathbb{F}}_2\backslash mathbb\{F\}\_2$ 上では、$nn$ 個のランダムに選択された $nn$ 次元ベクトルがフルランク行列を形成する確率 $PP$ は次のようになります。

$$P(n)=\prod _{k=0}^{n-1}(1-\frac{2^k}{2^n})P(n)\; =\; \backslash prod\_\{k=0\}^\{n-1\}\; \backslash left(1\; -\; \backslash frac\{2^k\}\{2^n\}\backslash right)$$

$nn$ が大きい場合（この例では $n=248n=248$）、この確率は定数に収束します（付録II）。

$$\underset{n\to \mathrm{\infty }}{\lim }P(n)\approx 0.28879\backslash lim\_\{n\; \backslash to\; \backslash infty\}\; P(n)\; \backslash approx\; 0.28879$$

これは、各ランダムな試行が約 28.9% の成功確率を持つことを意味します。平均して、攻撃者は線形独立なベクトルのセットを見つけるために約3.5回の試行で十分です。したがって、計算コストは非常に低く、攻撃者は条件を満たす行列 $AA$ を迅速に構築できます。

上位8ビットの countLegs を制御するには、ターゲット countLegs に基づいてランダムに生成された tokenId の範囲を調整するだけで十分です。

たとえば、偽造されたフィンガープリントの numLegs を0にしたい場合、$nn$ 個のランダムに生成された tokenId がすべて $2^{64}2^\{64\}$ 未満であることを確認するだけで済みます。この範囲の tokenId のレッグインクリメントは0であるため、ガウスの消去法ソリューション $xx$ がどのベクトルを選択しても、最終的な累積 numLegs は必然的に0になります。

攻撃分析

ホワイトハットレスキュー担当者は、複数のレスキュートランザクションを開始しました。簡単のため、以下の議論はこれらのトランザクションのうち1つに基づいています [3]。

コアロジックは、次の5つのステップで構成されます。

1. Aaveからフラッシュローンで0.23e8 WBTCと28e18 WETHを借入します。
2. 0.23e8 WBTCと28e18 WETHをpoWBTCコントラクトと0x1f8d_poWETHコントラクトに預け入れます。
3. 通常の positionIdList を使用して PanopticPool コントラクトの mintOptions() を呼び出し、資金を借入してレバレッジポジションを開きます。
4. 偽造された tokenId を渡して withdraw() を呼び出します。これらの偽造されたポジションは positionSize が0であるため、関数は tokenRequired を0として返します。これは、すべてのポジションに必要な合計担保が誤ってゼロとして計算されることを意味します。Meanwhile,これらの tokenId によって生成された s_positionsHash は、ステップ3で生成されたものとまったく同じであり、レスキュー担当者は負債を返済せずにすべての担保を取得できます。
5. フラッシュローンを返済し、次のラウンドを実行します。

要約

このインシデントは、2つの累積的な欠陥により、不正な担保引き出しが可能になったことを浮き彫りにしています。

• XORはハッシュの安全な集約関数ではありません。 Keccak256は衝突耐性がありますが、XORの線形性により、複数のハッシュのXOR合計はそのプロパティを継承しません。XORでターゲット値になる入力のセットを構築することは、${\mathbb{F}}_2\backslash mathbb\{F\}\_2$ 上の線形方程式のシステムを解くことに帰着し、計算上は単純です。ハッシュの合成には、衝突耐性を維持する操作（例：連結後の再ハッシュ）が必要です。
• ポジションIDの検証漏れ。 プロトコルは、渡された positionId が有効なオプションポジションに対応するかどうかを検証しませんでした。 $2^{64}2^\{64\}$ 未満の値は countLegs が0で positionSize が0であるため、偽造されたポジションは負債を発生させません。これにより、攻撃者はターゲットフィンガープリントと一致させながら、担保要件ゼロでヘルスチェックを通過することができました。

参照

1. https://x.com/Panoptic_xyz/status/1961187739866644524

2. https://cseweb.ucsd.edu/~mihir/papers/inchash.pdf

3. https://app.blocksec.com/explorer/tx/eth/0x67a45dfe5ff4b190058674d7c791bbdc48e889f319f937c24fa13a5f9093f088

付録

以下の2つの付録は、本文中のステートメント、すなわちXOR演算がベクトル加算に相当すること（付録I）およびランダム行列がフルランクである確率（付録II）の数学的説明と証明を提供します。

付録I

有限体 ${\mathbb{F}}_2=\{0,1\}\backslash mathbb\{F\}\_2\; =\; \backslash \{0,\; 1\backslash \}$ では、加算は2を法とする加算として定義されます。

観測によると、これは排他的論理和（XOR、記号 $\oplus \backslash oplus$）論理演算と同一です。

$nn$ 次元ベクトル空間 ${\mathbb{F}}_2^n\backslash mathbb\{F\}\_2^n$ （この場合 $n=248n=248$）では、2つのベクトル $u=[u_1,\dots ,u_n{]}^{T}u\; =\; [u\_1,\; \backslash dots,\; u\_n]^T$ と $v=[v_1,\dots ,v_n{]}^{T}v\; =\; [v\_1,\; \backslash dots,\; v\_n]^T$ の加算は、要素ごとの2を法とする加算として定義されます。

$$u+v=\left[\begin{array}{c}{u}_1+v_1(\mathrm{m}\mathrm{o}\mathrm{d}2)\\ \mathrm{⋮}\\ u_n+v_n(\mathrm{m}\mathrm{o}\mathrm{d}2)\end{array}\right]=\left[\begin{array}{c}{u}_1\oplus v_1\\ \mathrm{⋮}\\ u_n\oplus v_n\end{array}\right]=u\oplus vu\; +\; v\; =\; \backslash begin\{bmatrix\}\; u\_1\; +\; v\_1\; \backslash pmod\; 2\; \backslash \backslash \; \backslash vdots\; \backslash \backslash \; u\_n\; +\; v\_n\; \backslash pmod\; 2\; \backslash end\{bmatrix\}\; =\; \backslash begin\{bmatrix\}\; u\_1\; \backslash oplus\; v\_1\; \backslash \backslash \; \backslash vdots\; \backslash \backslash \; u\_n\; \backslash oplus\; v\_n\; \backslash end\{bmatrix\}\; =\; u\; \backslash oplus\; v$$

したがって、${\mathbb{F}}_2^n\backslash mathbb\{F\}\_2^\{n\}$ ベクトル空間では、ベクトル加算はベクトル成分のビットごとのXOR演算に相当します。

付録II

行列をフルランクにするには、これらの $nn$ 個のベクトルが線形独立である必要があります。

最初のベクトル $v_{1}v\_1$ は、ゼロベクトル以外の任意のベクトル ${\mathbb{F}}_2^n\backslash mathbb\{F\}\_2^n$ になり得ます。これは $2^n-12^n\; -\; 1$ の選択肢を提供します。2番目のベクトル $v_{2}v\_2$ は、$2^{1}2^1$ 個のベクトルを含む $\{v_1\}\backslash \{v\_1\backslash \}$ によってスパンされる部分空間に属してはなりません。これにより、$2^n-22^n\; -\; 2$ の選択肢が残ります。この論理に従うと、$kk$ 番目のベクトル $v_{k}v\_k$ は、前の $k-1k-1$ 個のベクトルによってスパンされる部分空間に属することはできず、$2^n-2^{k-1}2^n\; -\; 2^\{k-1\}$ の可能な選択肢があります。

そのような行列の総数（つまり、$GL(n,{\mathbb{F}}_2)GL(n,\; \backslash mathbb\{F\}\_2)$ の位数）は次のとおりです。

$$N=\prod _{k=0}^{n-1}(2^n-2^k)=(2^n-1)(2^n-2)(2^n-4)\cdots (2^n-2^{n-1})N\; =\; \backslash prod\_\{k=0\}^\{n-1\}\; (2^n\; -\; 2^k)\; =\; (2^n\; -\; 1)(2^n\; -\; 2)(2^n\; -\; 4)\backslash cdots(2^n\; -\; 2^\{n-1\})$$

そして、すべての可能な $n\times nn\; \backslash times\; n$ 行列の総数は $(2^n{)}^n=2^{n^2}(2^n)^n\; =\; 2^\{n^2\}$ です。

したがって、確率 $PP$ は次のようになります。

$$P=\frac{\prod _{k=0}^{n-1}(2^n-2^k)}{2^{n^2}}=\prod _{k=0}^{n-1}\left(\frac{2^n-2^k}{2^n}\right)=\prod _{k=0}^{n-1}(1-\frac{2^k}{2^n})P\; =\; \backslash frac\{\backslash prod\_\{k=0\}^\{n-1\}\; (2^n\; -\; 2^k)\}\{2^\{n^2\}\}\; =\; \backslash prod\_\{k=0\}^\{n-1\}\; \backslash left(\; \backslash frac\{2^n\; -\; 2^k\}\{2^n\}\; \backslash right)\; =\; \backslash prod\_\{k=0\}^\{n-1\}\; (1\; -\; \backslash frac\{2^k\}\{2^n\})$$

$j=n-kj\; =\; n\; -\; k$ と置くと、この式は次のように書き直すことができます。

$$P=\prod _{j=1}^n(1-\frac{1}{2^j})P\; =\; \backslash prod\_\{j=1\}^\{n\}\; \backslash left(1\; -\; \backslash frac\{1\}\{2^j\}\backslash right)$$

$n\to \mathrm{\infty }n\; \backslash to\; \backslash infty$ とすると、この積は定数に収束します。

$$P\approx 0.288788P\; \backslash approx\; 0.288788$$

これは、大きな $nn$ に対して、ランダム行列がフルランクである確率は約 28.9% であることを意味します。

BlockSecについて

BlockSecは、フルスタックのブロックチェーンセキュリティおよび暗号コンプライアンスプロバイダーです。私たちは、顧客がコード監査（スマートコントラクト、ブロックチェーン、ウォレットを含む）、リアルタイムでの攻撃の傍受、インシデントの分析、不正資金の追跡、およびプロトコルとプラットフォームのライフサイクル全体にわたるAML/CFT義務の遵守を支援する製品とサービスを構築しています。

BlockSecは、著名なカンファレンスで複数のブロックチェーンセキュリティ論文を発表し、DeFiアプリケーションの複数のゼロデイ攻撃を報告し、2000万ドル以上の救済をもたらした複数のハッキングを阻止し、数十億ドル相当の暗号資産を保護してきました。

• 公式ウェブサイト: https://blocksec.com/

• 公式Twitterアカウント: https://twitter.com/BlockSecTeam

• 🔗 BlockSec監査サービス : リクエストを送信

• 🔗 PhalconセキュリティAPP: デモを予約

• 🔗 Phalconコンプライアンス