#5 Yearn Finance Vorfall: Unsichere Arithmetik im Invarianten-Solver macht seinem Namen alle Ehre

Am 30. November 2025 wurde der yETH Weighted Stable Pool von Yearn Finance für über 9 Millionen US-Dollar ausgenutzt [1]. Die Hauptursachen waren unsichere Arithmetik im Invariantenlöser _calc_supply() und ein nicht deaktivierter Bootstrap-Pfad, der eine erneute Ausführung der Initialisierungslogik ermöglichte. Der offizielle Post-Mortem [2] listet fünf Punkte als Hauptursachen auf; wir stufen diese neu als zwei Mängel (die oben genannten Schwachstellen) und zwei architektonische Vorbedingungen ein, die nur in Anwesenheit dieser Mängel ausnutzbar wurden. Andere verfügbare Analysen konzentrieren sich auf schrittweise Details der Angriffstransaktionen. Zwischen High-Level-Zusammenfassungen und Details auf Transaktionsebene bleibt eine Lücke: Warum und wie hat der Angriff tatsächlich funktioniert? Dieser Beitrag schließt diese Lücke, indem er Simulationen mit Foundry und Python verwendet, um zu verfolgen, wie sich Schlüsselwerte Schritt für Schritt entwickeln und wo die Berechnungen fehlschlagen.

Diese Analyse leistet hauptsächlich die folgenden drei Beiträge:

1. Aufschlüsselung der Verluste nach Schwachstelle. Die beiden Schwachstellen sind nicht voneinander abhängig: Unsichere Arithmetik allein verursachte Verluste von ca. 8,1 Mio. US-Dollar (90% des Gesamtbetrags), während der Bootstrap-Pfad zusätzliche ca. 0,9 Mio. US-Dollar ermöglichte. Dies verdeutlicht, welche Schwachstelle primär war.
2. Neustrukturierung der Hauptursachen. Die fünf Hauptursachen des offiziellen Berichts werden besser als zwei Implementierungsfehler (die drei der fünf Punkte konsolidieren) plus zwei architektonische Vorbedingungen verstanden, die nur in Kombination mit den Fehlern ausnutzbar wurden.
3. Korrektur technischer Missverständnisse. Die Behauptung, dass "ein Unterlauf in der zweiten Iteration den Produktterm auf Null setzt", trifft nicht zu: Unsere Simulationen zeigen, dass das Produkt durch Rundung bei der Division auf Null gesetzt wird, nicht durch Unterlauf, und der Gewinn erzeugende Unterlauf tritt in einer ganz anderen Phase auf.

Der Rest dieses Beitrags ist wie folgt organisiert. Abschnitt 0x1 gibt einen Überblick über den gewichteten Stable-Pool von yETH und seinen Invariantenlöser. Abschnitt 0x2 analysiert die beiden Hauptursachen und ihre Fehlermodi. Abschnitt 0x3 verfolgt den dreiphasigen Angriff im Detail. Abschnitt 0x4 korrigiert zwei gängige Missverständnisse mit Simulationsbeweisen. Abschnitt 0x5 schließt mit Empfehlungen.

TL;DR

Hauptursachen: Zwei Schwachstellen wurden ausgenutzt, jedoch mit asymmetrischem Einfluss:

1. Unsichere Arithmetik in _calc_supply() (primär, ca. 8,1 Mio. US-Dollar). Die Funktion, die die yETH-Versorgung aus dem Poolzustand neu berechnet, enthält zwei arithmetische Fehler: Abrundung in unsafe_div() kann den internen Produktterm auf Null setzen, und Unterlauf in unsafe_sub() kann einen Zwischenwert auf eine riesige positive ganze Zahl umwickeln. Diese Schwachstelle allein reichte aus, um den yETH Weighted Stableswap Pool zu leeren.
2. Nicht deaktivierter Bootstrap-Pfad (sekundär, ca. 0,9 Mio. US-Dollar). Der Initialisierungszweig prev_supply == 0 wurde nach der Bereitstellung nie dauerhaft abgesperrt. Nachdem die erste Schwachstelle die Versorgung auf Null reduziert hatte, wurde dieser Pfad erreichbar und ermöglichte zusätzliche Gewinne aus dem yETH/WETH Curve Pool.

Innerhalb der unsicheren Arithmetik-Schwachstelle wurde nur der Abrundungsfehler (Fehlermodus A) in Phase 2 verwendet; der Unterlauffehler (Fehlermodus B) ist vom Bootstrap-Pfad abhängig, und zusammen ermöglichten sie Phase 3.

Der Angreifer führte eine dreiphasige Sequenz durch:

1. Vorbereitung: Verzerren Sie die Asset-Verteilung des Pools durch wiederholte Hinzufüge-/Entnahmezyklen, wodurch eine extreme Ungleichheit der virtuellen Salden entsteht.
2. Angebotsmanipulation: Ausnutzen der Abrundung in _calc_supply(), um das Produkt auf Null zu reduzieren, und dann die Gesamtversorgung durch eine Reihe von Präge-/Verbrennungsoperationen auf Null zu reduzieren. Alle LSTs des Pools wurden entnommen und danach in WETH getauscht, was zu Verlusten von ca. 8,1 Mio. US-Dollar führte.
3. Gewinnabschöpfung: Auslösen des Bootstrap-Pfads (prev_supply == 0) mit Staubablagerungen, Ausnutzen des Unterlaufs in _calc_supply(), um ca. 2,35 x 10⁵⁶ yETH zu prägen, die zum Leeren des yETH/WETH Curve Pools verwendet wurden, was zu Verlusten von ca. 0,9 Mio. US-Dollar führte.

Zwei gängige Missverständnisse, die korrigiert werden:

• "Die Invariante bricht, weil pow_up() und pow_down() unterschiedlich runden." Wir haben durch den Ersatz von pow_up() durch pow_down() in einer Foundry-Simulation verifiziert: Der Exploit funktioniert immer noch. Die Rundungsinkongruenz ist keine Hauptursache.
• "Ein Unterlauf in der zweiten Iteration lässt einen Zwischenterm auf Null zusammenfallen." Unsere Foundry- und Python-Simulationen zeigen, dass in der zweiten Iteration kein Unterlauf auftritt. Der tatsächliche Wert beträgt ca. 1,91e19 (nicht ca. 1,94e18 wie behauptet), ein legitimes Ergebnis einer korrekten Subtraktion. Was das Produkt auf Null setzt, ist die anschließende Abrundung bei der Division, nicht ein Unterlauf.

0x1 Hintergrund

Bei diesem Vorfall gingen Vermögenswerte aus zwei Pools verloren: dem yETH Weighted Stableswap Pool (ein Yearn Pool, der LSTs hält, ca. 8,1 Mio. US-Dollar Verlust) und dem yETH/WETH Curve Pool (ein Curve Stableswap Pool, ca. 0,9 Mio. US-Dollar Verlust). Der yETH Weighted Stableswap Pool ist die Stelle, an der die Kernschwachstelle liegt. Dieser Abschnitt gibt den Hintergrund, der zum Verständnis der Schwachstelle und des Exploits notwendig ist.

0x1.1 Virtuelle Salden und die Invariante

Das yETH-Protokoll ist ein Automated Market Maker (AMM) für Ethereum Liquid Staking Tokens (LSTs) [3]. Der betroffene yETH Weighted Stableswap Pool aggregiert mehrere LSTs in einem einzigen Pool: Benutzer zahlen LSTs ein und erhalten yETH als Pool-Share-Token.

Da jeder LST gestaktes ETH darstellt, das im Laufe der Zeit Belohnungen erwirtschaftet, ändert sich sein Wechselkurs im Verhältnis zu Basis-ETH. Um die Buchhaltung zu vereinheitlichen, definiert der Pool für jedes Asset einen virtuellen Saldo $x_{i}x\_i$: On-Chain-Saldo × Wechselkurs. Dies normalisiert alle Assets in Beacon-Chain-ETH-Einheiten. Die Summe aller virtuellen Salden wird mit $\sigma =\sum x_i\backslash sigma\; =\; \backslash sum\; x\_i$ bezeichnet.

Der Pool enthält 8 Assets (indiziert 0–7), jedes mit einem zugewiesenen Gewicht $w_{i}w\_i$:

Der Zustand des Pools wird durch eine gewichtete StableSwap-artige Invariante gesteuert [4]:

$$\begin{array}{cccc}& {Af}^n\sigma +D={Af}^{n}D+D\cdot \pi & & \text{(1)}\end{array}\backslash mathit\{Af\}^\{\backslash ,n\}\backslash ;\backslash sigma\; +\; D\; =\; \backslash mathit\{Af\}^\{\backslash ,n\}\backslash ;D\; +\; D\; \backslash cdot\; \backslash pi\; \backslash tag\{1\}$$

wobei:

• $DD$ der Skalierungsfaktor der Invariante ist, der direkt der gesamten yETH-Versorgung dieses Pools entspricht. Wenn der Pool perfekt ausbalanciert ist, gilt $D=\sigma D\; =\; \backslash sigma$.
• $\pi \backslash pi$ der gewichtete Produktterm ist, definiert als $\pi =D^n{\prod }_i{\left(\frac{w_i}{x_i}\right)}^{v_i}\backslash pi\; =\; D^n\; \backslash prod\_\{i\}\; \backslash left(\backslash frac\{w\_i\}\{x\_i\}\backslash right)^\{v\_i\}$, wobei $w_{i}w\_i$ das Gewicht des Assets i und $v_i=w_i\cdot nv\_i\; =\; w\_i\; \backslash cdot\; n$ ist.
• $Af\backslash mathit\{Af\}$ der Verstärkungsfaktor ist, ein einzelner Protokollparameter (nicht $A\times fA\; \backslash times\; f$). ${Af}^n\backslash mathit\{Af\}^\{\backslash ,n\}$ bezeichnet diesen Faktor, hoch n, wobei n die Anzahl der Assets ist (in diesem Pool 8). Er steuert die Kurvenform zwischen konstant-sum (nahe dem Gleichgewicht) und konstant-product (an den Extremen).

Die Schlüsseleigenschaft: $DD$ hat keine geschlossene Form. Es muss numerisch gelöst werden. Dieser Löser, _calc_supply(), ist die Stelle, an der sich die arithmetische Schwachstelle befindet.

0x1.2 Der Invariantenlöser

Das Protokoll berechnet $DD$ durch eine Festpunktiteration, die auf 256 Runden begrenzt ist. Dieser Algorithmus ist im Code als _calc_supply() implementiert (detailliert in Abschnitt 0x2.1). Jede Runde führt drei Schritte aus:

Schritt 1: Schätzung der Versorgung aktualisieren.

$$\begin{array}{cccc}& D_{m+1}=\frac{{Af}^n\cdot \sigma -D_m\cdot {\pi }_m}{{Af}^n-1}& & \text{(2)}\end{array}D\_\{m+1\}\; =\; \backslash frac\{\backslash mathit\{Af\}^\{\backslash ,n\}\; \backslash cdot\; \backslash sigma\; -\; D\_m\; \backslash cdot\; \backslash pi\_m\}\{\backslash mathit\{Af\}^\{\backslash ,n\}\; -\; 1\}\; \backslash tag\{2\}$$

Schritt 2: Produktterm aktualisieren, um die neue Versorgung anzupassen.

$$\begin{array}{cccc}& {\pi }_{m+1}={\pi }_m\cdot {\left(\frac{D_{m+1}}{D_m}\right)}^n& & \text{(3)}\end{array}\backslash pi\_\{m+1\}\; =\; \backslash pi\_m\; \backslash cdot\; \backslash left(\backslash frac\{D\_\{m+1\}\}\{D\_m\}\backslash right)^n\; \backslash tag\{3\}$$

Schritt 3: Konvergenz prüfen.

Wenn , gib $D_{m}D\_\{m\}$ zurück; andernfalls wiederhole von Schritt 1.

Die Anfangswerte $D_{0}D\_0$, ${\pi }_0\backslash pi\_0$ und $\sigma \backslash sigma$ beeinflussen die frühen Iterationen; obwohl sie theoretisch für die endgültige Konvergenz irrelevant sind, beeinflussen sie die Ergebnisse in der Praxis aufgrund endlicher Iterationen und Festkomma-Arithmetik.

Die Implementierung verwendet Festkomma-Ganzzahloperationen: Division rundet ab, und Subtraktion schützt nicht vor Unterlauf. Unter normalen Poolbedingungen bleiben die Zwischenwerte in sicheren Bereichen. Unter extremen Poolzuständen tun sie das nicht. Abschnitt 0x2.1 analysiert diese Fehlermodi im Detail.

0x1.3 Die drei Schnittstellen und der Invariantenlöser

Das Protokoll stellt drei Einstiegspunkte bereit, die den Poolzustand beeinflussen, indem sie den gewichteten Produktterm $\pi \backslash pi$ (im Code als vb_prod gespeichert) aktualisieren:

Die Asymmetrie ist wichtig: add_liquidity() erlaubt Einzahlungen in beliebigen Proportionen (es kann den Pool massiv verzerren), während remove_liquidity() immer proportional abzieht. Wiederholte Zyklen von Hinzufügen/Entfernen können daher den Pool immer weiter in immer unausgeglichenere Zustände treiben.

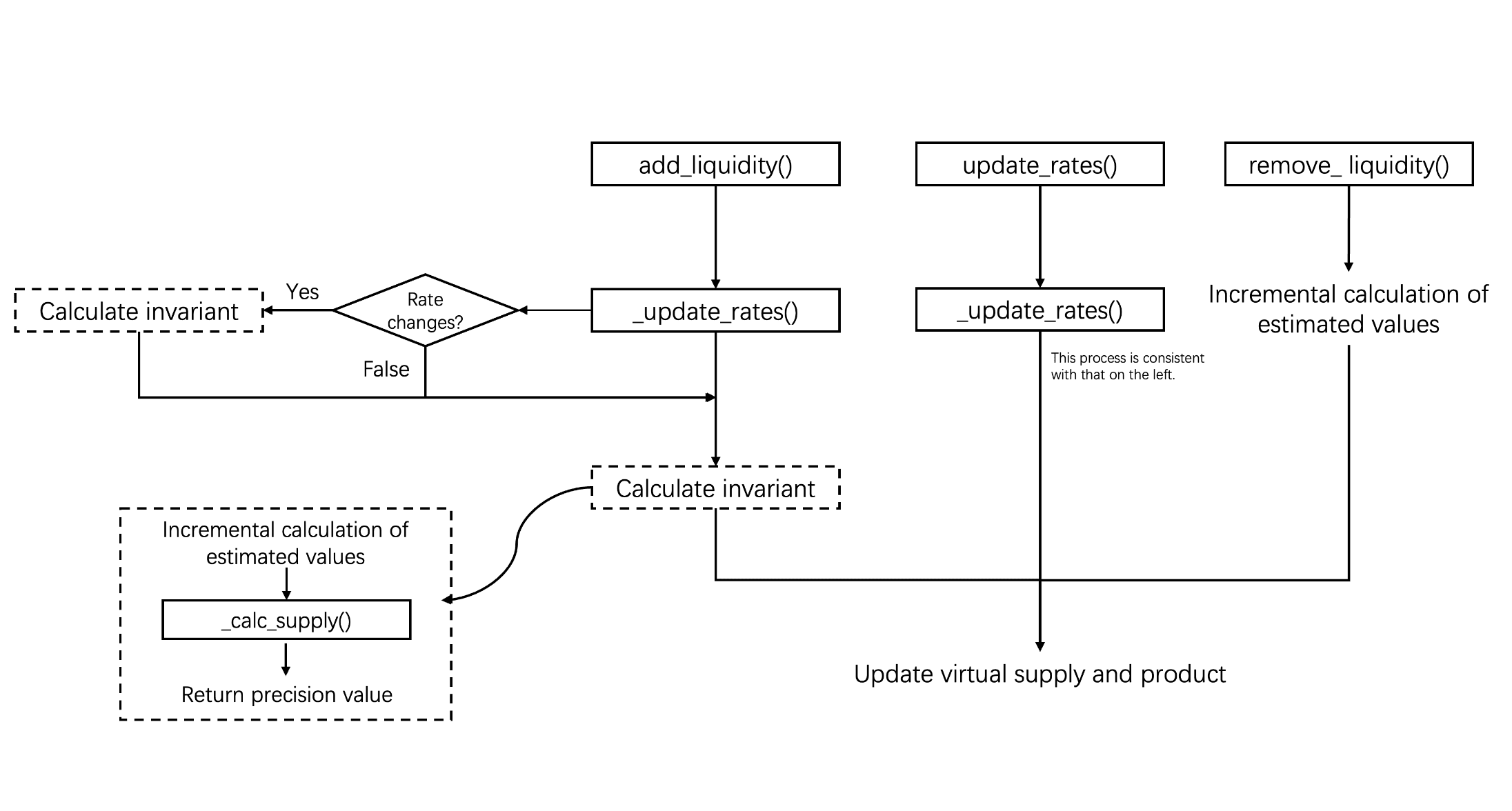
Der Mechanismus zur Aktualisierung der Kurse

Wie oben diskutiert, werden die virtuellen Salden ($x_{i}x\_i$) basierend auf den Wechselkursen der LSTs berechnet. Daher ist es wichtig, die Methode zur Aktualisierung der Kurse zu verstehen.

Insbesondere können die Funktionen add_liquidity() und update_rates() die Kurse über die interne Funktion _update_rates() aktualisieren, während die Funktion remove_liquidity() keine Raten-Synchronisation durchführt.

• add_liquidity() ruft _update_rates() auf, bevor kritische Operationen ausgeführt werden, um sicherzustellen, dass die Asset-Wechselkurse mit dem neuesten Stand synchronisiert sind.
• update_rates() ermöglicht manuelle Ratenaktualisierungen.

Die Funktion _update_rates() prüft, ob die im Vertrag aufgezeichneten Wechselkurse mit den externen Kursen übereinstimmen. Wenn eine Diskrepanz festgestellt wird, löst sie eine Neuberechnung der virtuellen Salden aus und aktualisiert anschließend die Invariante; andernfalls wird der Aktualisierungsprozess übersprungen.

Wie jede Schnittstelle mit π umgeht

Basierend darauf, wie sie die Invariante beeinflussen, können diese drei Funktionen in zwei Kategorien eingeteilt werden. Insbesondere erlauben add_liquidity() und update_rates() nicht-proportionale Änderungen der virtuellen Salden und erfordern daher eine iterative Neuberechnung des Angebots $DD$ und des Produkts $\pi \backslash pi$. Im Gegensatz dazu zieht remove_liquidity() Liquidität proportional ab und erfordert keine iterative Berechnung.

Die Basisformel zur Berechnung des Produkts von Grund auf lautet:

$$\begin{array}{cccc}& \pi =\prod _i{\left(\frac{D\cdot w_i}{x_i}\right)}^{n\cdot w_i}& & \text{(4)}\end{array}\backslash pi\; =\; \backslash prod\_\{i\}\; \backslash left(\backslash frac\{D\; \backslash cdot\; w\_i\}\{x\_i\}\backslash right)^\{n\; \backslash cdot\; w\_i\}\; \backslash tag\{4\}$$

wobei $DD$ das Angebot, $w_{i}w\_i$ das Gewicht von Asset $ii$, $x_{i}x\_i$ sein virtueller Saldo (im Code als vb[i] gespeichert) und n die Anzahl der Assets ist. Diese Form ist algebraisch äquivalent zur Definition in Abschnitt 0x1.1, wobei $D^{n}D^n$ in das Produkt verteilt ist.

1. add_liquidity() hat zwei Pfade (Code in Abschnitt 0x2.2 gezeigt):

• Bootstrap-Pfad (wenn prev_supply == 0): Berechnet vb_prod von Grund auf neu anhand der Gleichung (4). Dieser Pfad, der nach der Bereitstellung zugänglich blieb, ist die Zustandsverwaltungs-Schwachstelle, die in Abschnitt 0x2.2 diskutiert wird.
• Normaler Pfad (wenn prev_supply > 0): Der Berechnungsprozess ist in zwei Schritte unterteilt:

  • a) Verwendet eine inkrementelle Aktualisierung basierend auf dem Verhältnis von altem zu neuem virtuellen Saldo:

    $$\begin{array}{cccc}& {\pi }_{\text{gesch}\ddot{\text{a}}\text{tzt}}=\pi \cdot \prod _{i=0}^{n-1}{\left(\frac{x_i}{x_i^{\mathrm{\prime }}}\right)}^{w_i\cdot n}& & \text{(5)}\end{array}\backslash pi\_\{\backslash text\{geschätzt\}\}\; =\; \backslash pi\; \backslash cdot\; \backslash prod\_\{i=0\}^\{n-1\}\; \backslash left(\backslash frac\{x\_i\}\{x\_i\text{'}\}\backslash right)^\{w\_i\; \backslash cdot\; n\}\; \backslash tag\{5\}$$

    wobei $x_{i}x\_i$ und $x_i^{\mathrm{\prime }}x\_i\text{'}$ die virtuellen Salden vor und nach der Einzahlung sind.

  • b) Kalibriert iterativ den genauen Wert, indem _calc_supply() mit dieser Schätzung als Eingabe aufgerufen wird, wobei die Invariante $DD$ und der exakte Wert von $\pi \backslash pi$ neu berechnet werden.

2. update_rates() wird ausgelöst, wenn sich die Wechselkurse ändern, was zur Aktualisierung der virtuellen Salden der entsprechenden Assets führt. Sein nachfolgender Berechnungsfluss folgt dem normalen Pfad von add_liquidity(), d.h. die Invariante wird iterativ neu berechnet. Darüber hinaus prägt oder verbrennt der Vertrag basierend auf dem neu berechneten Angebot yETH, um sicherzustellen, dass das Liquiditätsangebot mit dem aktualisierten virtuellen Saldenzustand konsistent bleibt.

3. remove_liquidity() berechnet vb_prod immer von Grund auf neu anhand der Gleichung (4), nachdem jeder virtuelle Saldo proportional reduziert wurde.

0x2 Hauptursachenanalyse

Zwei Schwachstellen wurden ausgenutzt, mit unterschiedlichen Rollen und Auswirkungen. Die primäre Hauptursache war ein Rechenfehler im Invariantenlöser _calc_supply(), der zwei Fehlermodi hatte: (A) Abrundung konnte das Produkt auf Null setzen, wodurch die Invariante zu einem konstant-sum-Modell degenerierte und zu übermäßiger LP-Prägung (Angebotsinflation) führte; und (B) ein Unterlaufzustand konnte ebenfalls das Angebot aufblähen. Nur Fehlermodus A wurde in Phase 2 (ca. 8,1 Mio. US-Dollar) verwendet. Fehlermodus B war abhängig von der sekundären Schwachstelle.

Die sekundäre Hauptursache war ein Zustandsverwaltungsfehler: Der Initialisierungszweig des Pools blieb erreichbar. Nachdem Phase 2 das Angebot auf Null reduziert hatte, kombinierte Fehlermodus B mit dem Bootstrap-Pfad, um zusätzliche Verluste von ca. 0,9 Mio. US-Dollar zu ermöglichen (Phase 3).

0x2.1 Unsichere Arithmetik in _calc_supply() (Primär)

Abbildung 2 bildet die Implementierung von _calc_supply() auf das mathematische Verfahren aus Abschnitt 0x1.2 ab und annotiert die beiden unten analysierten arithmetischen Fehlerstellen:

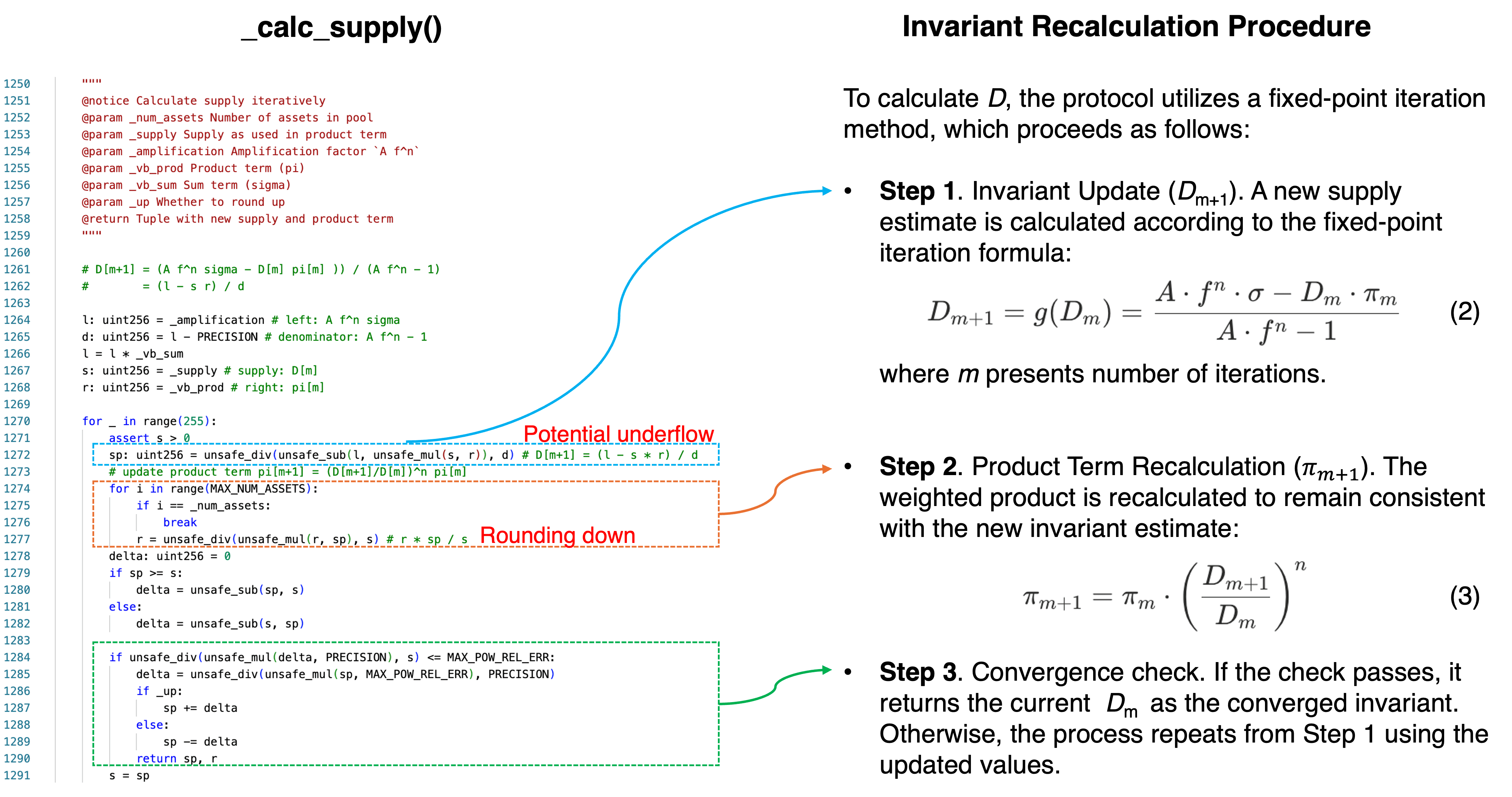
Die Codevariablen entsprechen den mathematischen Begriffen wie folgt:

Die kritischen Ausdrücke sind:

sp = unsafe_div(unsafe_sub(l, unsafe_mul(s, r)), d)   # Schritt 1: D[m+1]
r  = unsafe_div(unsafe_mul(r, sp), s)                 # Schritt 2: π-Aktualisierung (pro Asset)

Es existieren zwei arithmetische Fehlermodi innerhalb dieser Funktion, die unterschiedliche Zeilen ansprechen und unterschiedliche Effekte erzielen. Beide erfordern, dass der Pool in einem extremen Zustand ist, um ausgelöst zu werden.

Unter normalen Bedingungen verhält sich die Iteration korrekt: l - s * r ist ein moderater positiver Wert, und die Iteration konvergiert in wenigen Runden.

1. Fehlermodus A: Abrundung setzt das Produkt auf Null

In Schritt 2 wird das Produkt pro Asset aktualisiert als:

r = unsafe_div(unsafe_mul(r, sp), s)   # r = r * sp / s

Da unsafe_div() Ganzzahl-Division durchführt, rundet sie immer ab. Wenn der Pool stark unausgeglichen ist und sp viel kleiner als s ist (wie es nach einer manipulierten großen Einzahlung geschieht), kann der Zähler r * sp kleiner als der Nenner s werden. Ganzzahl-Division ergibt dann r = 0.

Sobald r Null ist, bleibt es für alle nachfolgenden Iterationen Null. Der Produktterm $\pi \backslash pi$ ist permanent kollabiert.

Eine häufige falsche Zuschreibung behauptet, dass dieser Fehler von einer Rundungsinkongruenz zwischen pow_up() und pow_down() herrührt. Abschnitt 0x4 liefert Beweise dafür, dass dies falsch ist.

2. Fehlermodus B: Unterlauf bläht das Angebot auf

In Schritt 1 wird die neue Angebotsschätzung berechnet als:

sp = unsafe_div(unsafe_sub(l, unsafe_mul(s, r)), d)   # sp = (l - s*r) / d

Die Subtraktion l - s*r ${Af}^n\cdot \sigma -D_m\cdot {\pi }_m\backslash mathit\{Af\}^\{\backslash ,n\}\; \backslash cdot\; \backslash sigma\; -\; D\_m\; \backslash cdot\; \backslash pi\_m$ in Gleichung 2. Unter normalen Bedingungen ist dies positiv. Wenn der Pool jedoch einen degenerierten Zustand mit Null-Angebot erreicht, berechnet der Initialisierungszweig in add_liquidity() (detailliert in Abschnitt 0x2.2) den Produktterm von Grund auf neu, und die relativen Größen können sich umkehren.

Insbesondere wenn add_liquidity() auf einem Null-Angebot-Pool mit Staubbeträgen aufgerufen wird, ruft der Initialisierungszweig _calc_vb_prod_sum() auf, um frische Werte anhand der Gleichung (4) (Abschnitt 0x1.3) zu berechnen. Bei winzigen Einzahlungen ist vb_sum winzig (z.B. 16), aber die Division durch fast Null-Salden und die Potenzierung zu hohen Potenzen verstärkt das Produkt auf einen unverhältnismäßig großen Wert (z.B. ~9,13e20). Wenn s * r größer als l ist, ergibt die Subtraktion ein mathematisch negatives Ergebnis.

Da unsafe_sub() eine Subtraktion in ungeprüfter uint256-Arithmetik durchführt, wickelt sich ein negatives Ergebnis zu einer riesigen positiven ganzen Zahl (nahe $2^{256}2^\{256\}$) um. Dieser gewickelte Wert breitet sich durch die Division und nachfolgende Iterationen aus und erzeugt eine absurd große Angebotsschätzung, die das Protokoll dann als echte yETH-Tokens prägt.

Eine häufige Behauptung besagt, dass ein solcher Unterlauf in der zweiten Iteration eines bestimmten Angebotsmanipulationsschritts auftritt. Abschnitt 0x4 zeigt, dass diese Behauptung falsch ist: Der tatsächliche Unterlauf, der das Angebot aufbläht, tritt in einem völlig anderen Kontext auf (Phase 3 des Angriffs).

3. Wie diese Fehler den Angriff ermöglichen

Diese beiden Fehlermodi wirken in verschiedenen Phasen des Exploits mit unterschiedlichen Gewinnbeiträgen:

• Fehlermodus A (Phase 2, ca. 8,1 Mio. US-Dollar): Wenn der Angreifer in einen stark unausgeglichenen Pool einzahlt, wird der Produktterm auf Null gesetzt, was dazu führt, dass _calc_supply() ein aufgeblähtes Angebot zurückgibt. Das Protokoll prägt dem Angreifer übermäßig yETH. Diese Schwachstelle allein, ohne jegliche Beteiligung des Bootstrap-Pfads, ermöglichte es dem Angreifer, den yETH Weighted Stableswap Pool seiner LST-Assets zu leeren.

• Fehlermodus B (Phase 3, ca. 0,9 Mio. US-Dollar): Nachdem das Angebot auf Null reduziert wurde, berechnet der Bootstrap-Pfad durch Staubablagerungen einen großen Produktterm neu, was zu einer negativen Subtraktion führt. Das Protokoll prägt eine astronomisch hohe Menge yETH, die der Angreifer verwendet, um den separaten yETH/WETH Curve Pool zu leeren.

Die Abhängigkeit ist unidirektional: Fehlermodus A ist unabhängig ausnutzbar und verursachte 90% der Verluste, während Fehlermodus B Fehlermodus A erfordert, um zuerst das Angebot auf Null zu treiben.

0x2.2 Nicht deaktivierter Bootstrap-Pfad (Sekundär)

Die Funktion add_liquidity() enthält einen Zweig für die erste Einzahlung des Pools:

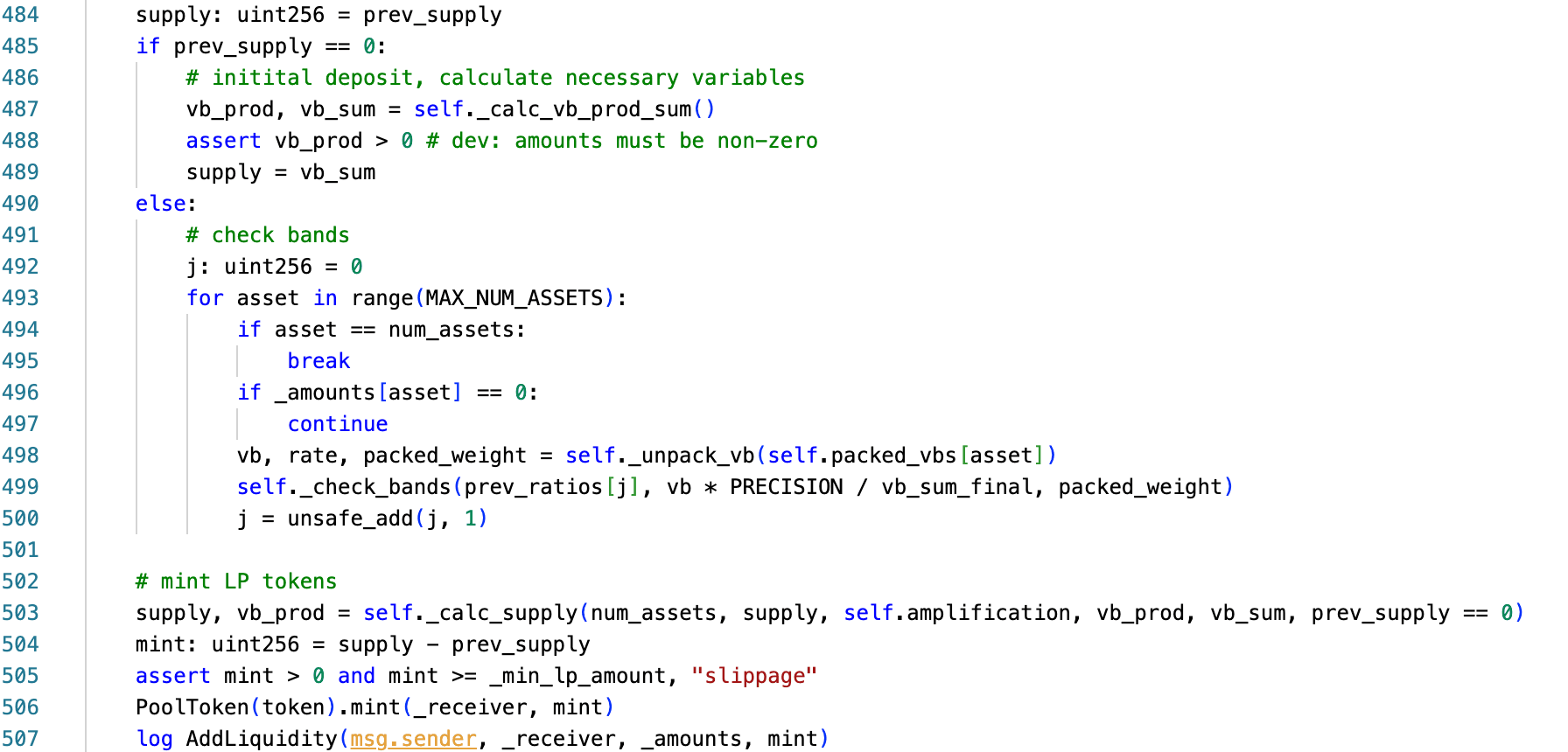
Die Logik kann wie folgt abstrahiert werden:

if prev_supply == 0:
    # Bootstrap-Pfad — berechnet vb_prod und vb_sum von Grund auf
    vb_prod, vb_sum = _calc_vb_prod_sum(balances, rates, weights, ...)
    supply = vb_sum
else:
    # Normaler Pfad — verwendet gespeichertes vb_prod, führt inkrementelle Prüfungen durch
    ...

# Nach beiden Zweigen aufgerufen, mit prev_supply == 0 als Flag
supply, vb_prod = _calc_supply(num_assets, supply, amplification, vb_prod, vb_sum, prev_supply == 0)

Wenn prev_supply == 0, umgeht die Funktion gespeicherte Zustände und berechnet vb_prod und vb_sum von Grund auf neu über _calc_vb_prod_sum(), unter Verwendung der Gleichung (4) (Abschnitt 0x1.3). Dieser Bootstrap-Zweig war für eine einmalige Verwendung während der Poolinitialisierung gedacht, wurde aber nach der ersten Einzahlung nie dauerhaft abgesperrt.

Wenn die Gesamtversorgung auf Null reduziert werden kann (durch eine beliebige Kombination von Verbrennungen und Entnahmen), wird der Zweig wieder erreichbar. Ein Angreifer, der diesen Pfad erneut betritt, kontrolliert die Anfangsbedingungen, die an _calc_supply() übergeben werden, und kann möglicherweise die oben beschriebenen arithmetischen Fehler unter Parametern auslösen, die während des normalen Poolbetriebs niemals auftreten würden.

Dies ist ein bekanntes Schwachstellenmuster. Im August 2023 war der Balancer V2-Vorfall ähnlich auf die Reduzierung der Versorgung auf Null angewiesen, um interne Raten zurückzusetzen, was es dem Angreifer ermöglichte, die Initialisierungslogik zu künstlich günstigen Parametern neu einzugeben [6]. Ob ein bereitgestellter Pool in seinen Anfangszustand zurückversetzt werden kann und welche Invarianten dabei gelten, ist eine Frage, die Protokolldesigner explizit angehen müssen.

0x3 Angriffsanalyse

Der Exploit entfaltet sich über eine koordinierte Abfolge von Angriffstransaktionen [5], die in drei Phasen organisiert sind. Jede Phase baut auf dem von der vorherigen Phase etablierten Zustand auf.

0x3.1 Phase 1: Verzerren des Pools (Vorbereitung)

Ziel: Extreme Ungleichheit bei den virtuellen Salden der Assets schaffen.

Die folgende Abbildung zeigt den Transaktionsverlauf für diese Phase (der Flash-Loan-Schritt wird aus Platzgründen weggelassen):

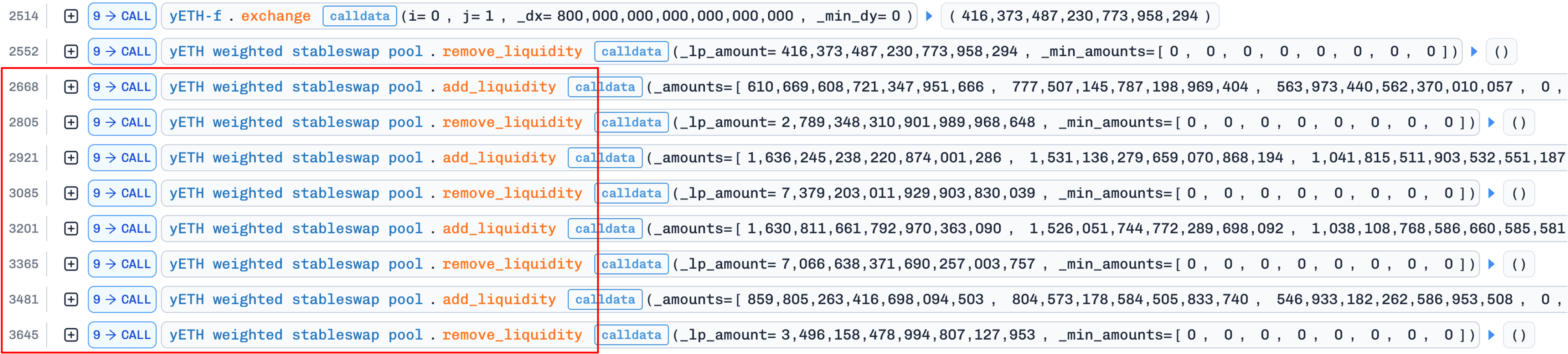
Der Angreifer leiht sich zunächst große Mengen an LST-Assets über Flash-Loans von Balancer und Aave, insbesondere 5.500e18 wstETH, 3.100e18 WETH, 1.800e18 rETH, 2.000e18 ETHx und 200e18 cbETH.

Als nächstes tauscht der Angreifer ungefähr 800e18 WETH gegen etwa 416e18 yETH im yETH/WETH Curve Pool und verwendet dann das erworbene yETH, um Liquidität aus dem Pool zu entnehmen.

Die Kernmanipulation nutzt die Schnittstellenasymmetrie aus, die in Abschnitt 0x1 (Hintergrund) beschrieben ist: add_liquidity() erlaubt Einzahlungen in beliebiger Proportion, während remove_liquidity() Assets proportional nach Poolgewicht abzieht (im roten Rechteck in der obigen Abbildung hervorgehoben). Durch wiederholtes Durchlaufen von Hinzufügen → Entfernen, Einzahlen nur ausgewählter Assets, während alle Assets proportional abgezogen werden, treibt der Angreifer den Pool schrittweise in einen stark unausgeglichenen Zustand:

Die Assets 3 (cbETH), 6 (WOETH) und 7 (mETH) wurden um über 98% erschöpft. Diese Ungleichheit zieht nicht direkt Profit ab. Sie schafft die numerischen Voraussetzungen für die nächste Phase.

0x3.2 Phase 2: Kollabierende Versorgung auf Null (ca. 8,1 Mio. US-Dollar)

Ziel: Das Invariantenprodukt auf Null treiben und dann die yETH-Versorgung auf Null reduzieren. Diese Phase nutzt nur die primäre Schwachstelle (unsichere Arithmetik) aus und verursachte ca. 90% der Gesamtverluste.

Diese Phase verwendet einen wiederholten Fünf-Schritte-Zyklus, der dreimal ausgeführt wird:

1. Produkt verderben durch add_liquidity();
2. Voraussetzung für Korrektur schaffen durch add_liquidity();
3. Produkt zurücksetzen durch remove_liquidity() mit 0 yETH;
4. Versorgung korrigieren durch update_rates();
5. Assets abziehen durch remove_liquidity().

Die folgende Abbildung zeigt den Transaktionsverlauf, wo drei Wiederholungen des Fünf-Schritte-Zyklus deutlich sichtbar sind:

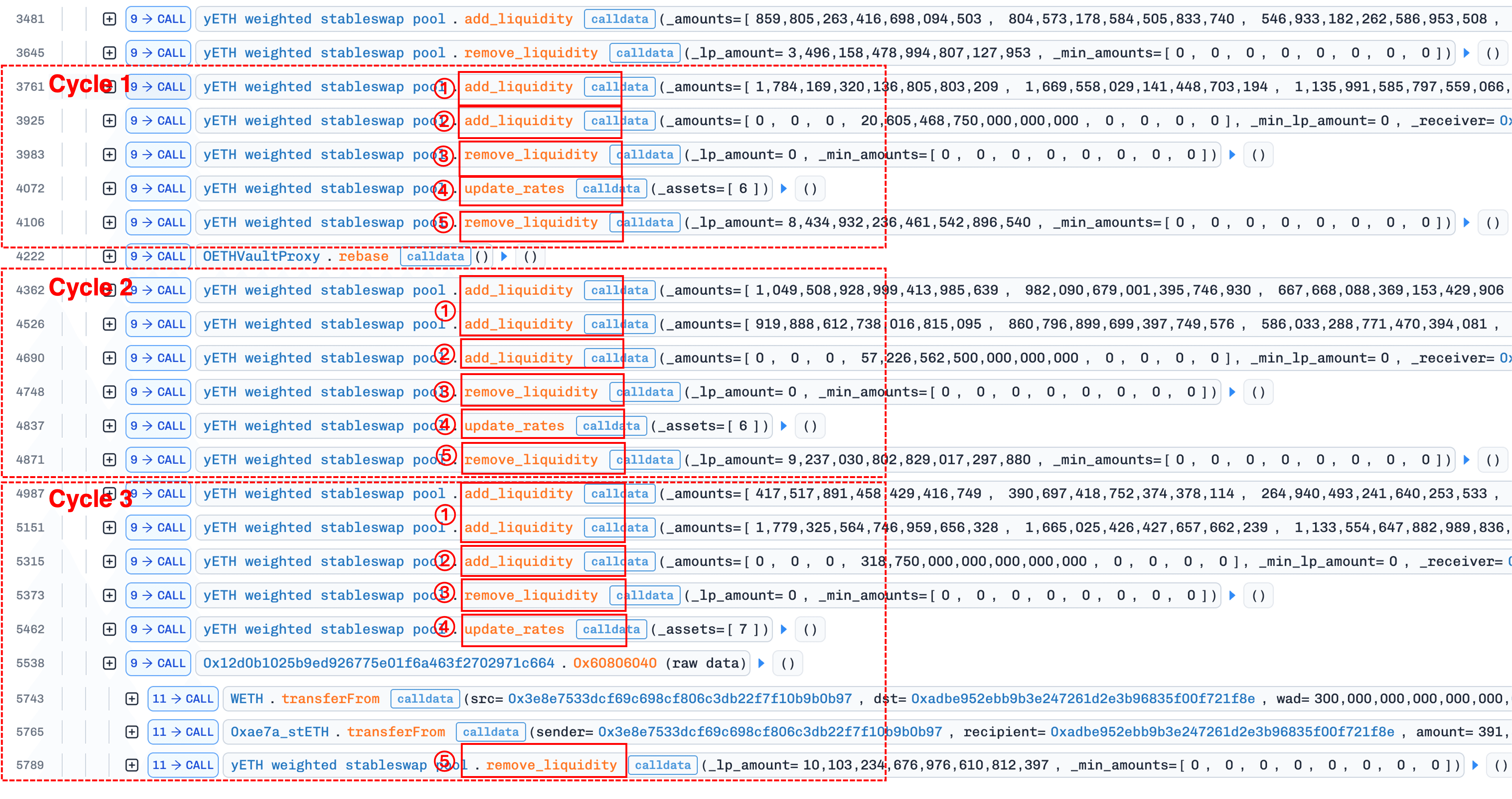
1. Produkt verderben durch add_liquidity()

Der Angreifer zahlt große Mengen an Assets mit hohem Gewicht (Indizes 0, 1, 2, 4, 5: sfrxETH, wstETH, ETHx, rETH, apxETH) ein, jeweils etwa das Dreifache ihres aktuellen virtuellen Saldos.

add_liquidity() schätzt den neuen Produktterm über die inkrementelle Aktualisierung in Gleichung (5) (Abschnitt 0x1.3). Da $x_i^{\mathrm{\prime }}\gg x_{i}x\_i\text{'}\; \backslash gg\; x\_i$ für Assets mit hohem Gewicht gilt, sind die Verhältnisse $(x_i\mathrm{/}{x}_i^{\mathrm{\prime }})(x\_i\; /\; x\_i\text{'})$ allesamt Brüche weit unter 1, hoch große Potenzen. Dies treibt ${\pi }_{\text{neu}}\backslash pi\_\{\backslash text\{neu\}\}$ von ca. 42e18 auf ca. 0,00353e18, ein fast null geschätztes Produkt.

Dieses winzige Produkt tritt in _calc_supply() ein. In der Iteration trifft die Produktaktualisierung r = r * sp / s auf die Abrundungsbedingung, die in Abschnitt 0x2 (Hauptursachenanalyse) beschrieben ist: Der Zähler fällt unter den Nenner, und die Ganzzahl-Division schneidet r auf Null. Die Funktion gibt ein Null-Produkt und ein aufgeblähtes Angebot (≈vb_sum) zurück, was dazu führt, dass das Protokoll yETH überprägt.

2. Voraussetzung für Korrektur schaffen durch add_liquidity()

Der Angreifer fügt eine einseitige Liquidität für Asset-Index 3 (cbETH, ein erschöpftes Asset mit geringem Gewicht) hinzu und zahlt etwa das 6,5-fache des aktuellen Pool-Saldos dieses Assets ein. Dies bringt nur wenige yETH-Tokens ein, gleicht aber den Pool genug aus, dass die nächste Iteration nicht wild oszilliert.

Ohne diesen Schritt würde selbst nach dem Zurücksetzen des Produkts auf einen Nicht-Null-Wert in Schritt 3 die Iteration in Schritt 4 aufgrund heftiger Oszillationen durch die extreme Ungleichheit immer noch ein Null-Produkt erzeugen. Unsere Foundry-Simulation bestätigt dies: Das Überspringen von Schritt 2 führt dazu, dass die Korrektur in Schritt 4 fehlschlägt.

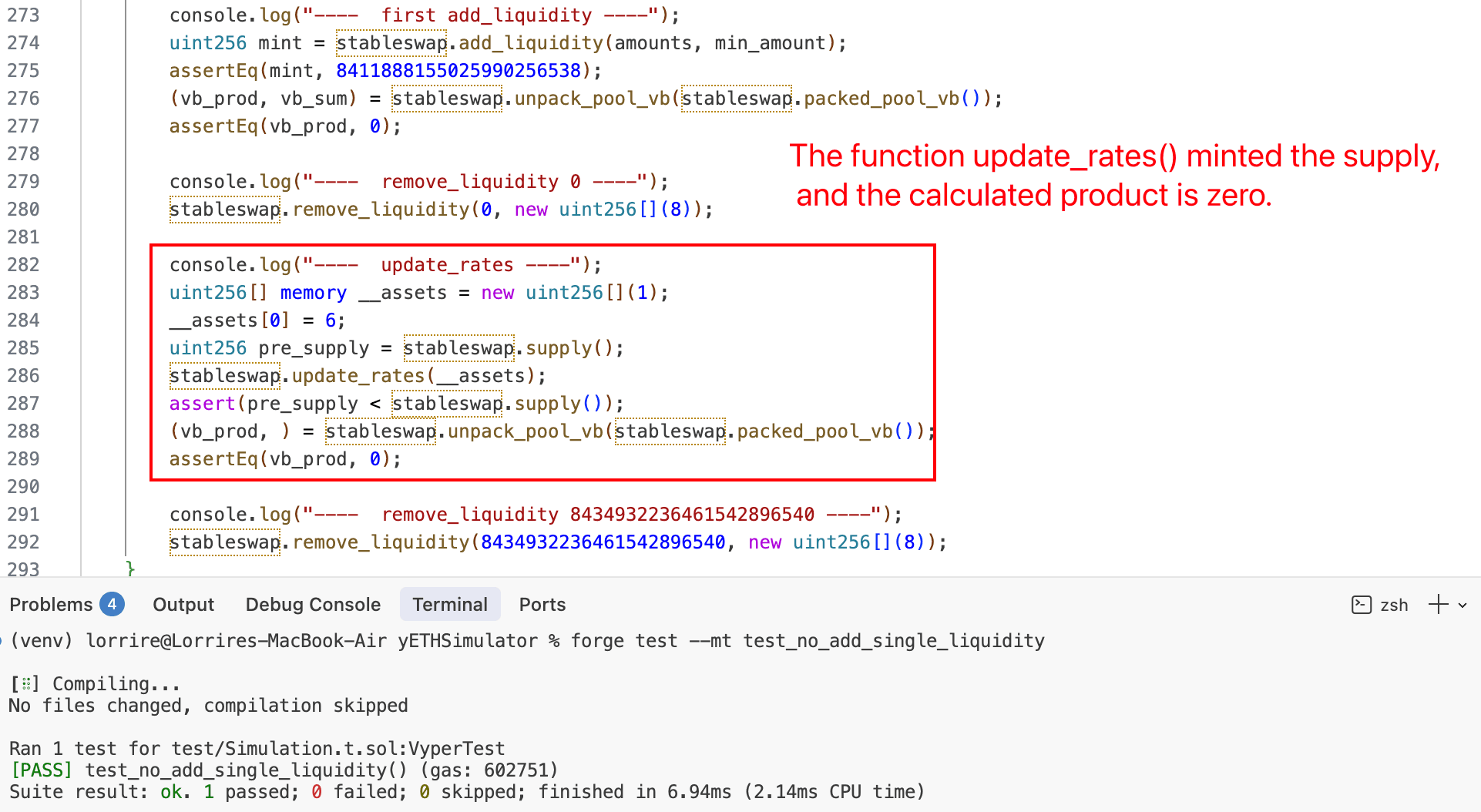
3. Produkt zurücksetzen durch remove_liquidity() mit 0 yETH

Der Angreifer ruft remove_liquidity() mit dem Betrag 0 auf. Es werden keine Token abgezogen, aber die Funktion berechnet vb_prod neu aus dem aktuellen Poolzustand anhand der Gleichung (4) (Abschnitt 0x1.3). Da die virtuellen Salden nicht Null sind, erzeugt dies ein Nicht-Null-Produkt (≈9,09e19) und überschreibt den verfälschten Null-Wert.

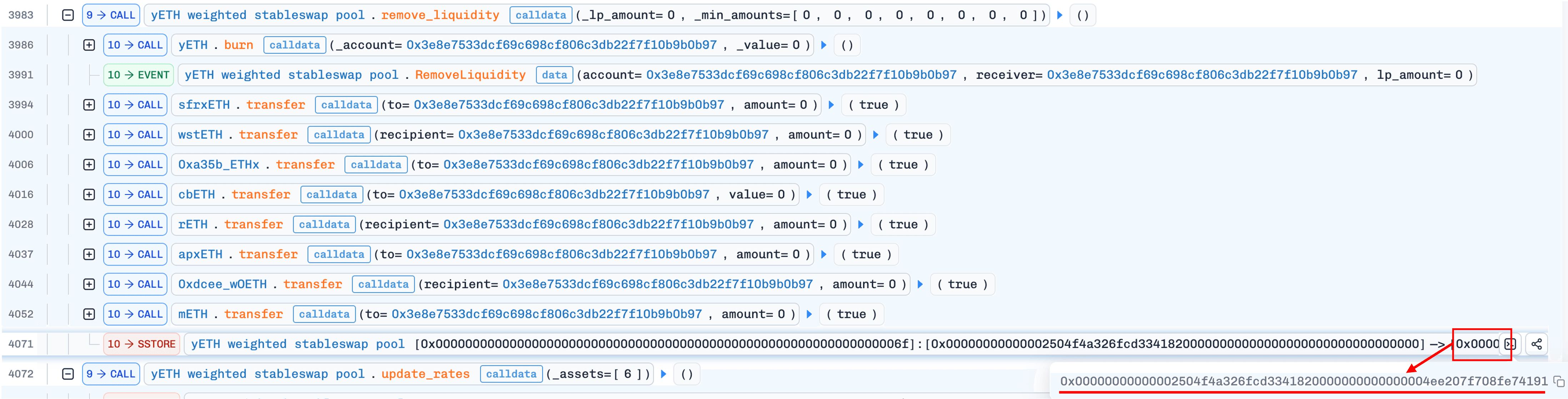
4. Versorgung korrigieren durch update_rates()

Der Angreifer ruft update_rates() für Asset-Index 6 (WOETH) oder 7 (mETH) auf. Wenn sich der Wechselkurs seit der letzten Aktualisierung geändert hat, löst die Funktion _calc_supply() mit dem wiederhergestellten (Nicht-Null-) Produkt aus. Dieses Mal konvergiert die Iteration korrekt und liefert einen Versorgungswert, der deutlich niedriger ist als der aktuelle aufgeblähte Wert. Die Differenz wird vom yETH-Staking-Vertrag verbrannt. Laut dem offiziellen Post-Mortem [2] handelt es sich hierbei um Protocol-Owned Liquidity (POL), was bedeutet, dass die Verbrennungen die Position des Protokolls und nicht die Bestände des Angreifers reduzieren. Diese Asymmetrie ist entscheidend: Jeder Zyklus reduziert die Gesamtversorgung, während das yETH-Guthaben des Angreifers intakt bleibt.

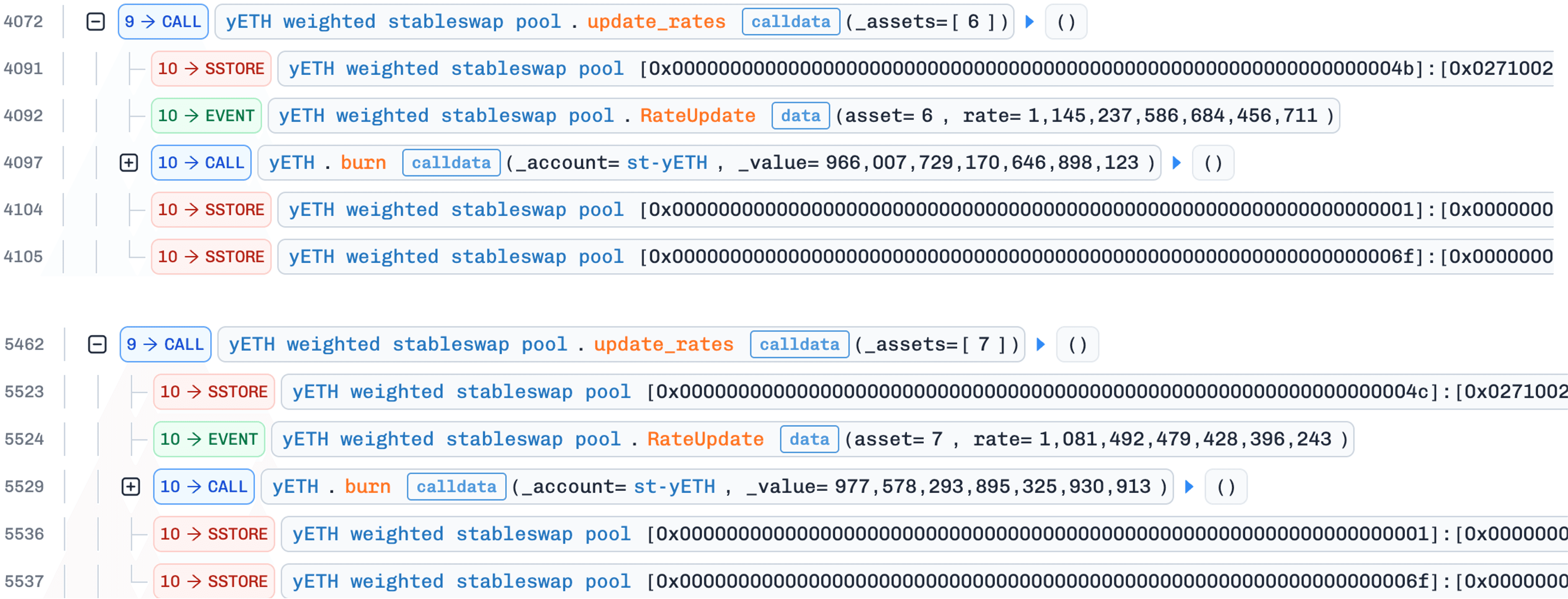
Die Raten-Diskrepanz selbst ist keine Gewinnquelle; sie dient rein als Auslösemechanismus. Von den drei Pool-Schnittstellen rufen nur add_liquidity() und update_rates() _calc_supply() auf; remove_liquidity() verwendet proportionale Skalierung und tut dies nicht. Nachdem Schritt 3 ein Nicht-Null-Produkt wiederhergestellt hat, muss der Angreifer _calc_supply() auslösen, ohne zusätzliche Assets einzuzahlen. Das Aufrufen von update_rates() mit einer veralteten Rate erreicht genau dies: Die Ratenänderung löst die Neuberechnung des Angebots ohne Kosten für den Angreifer aus.

Dies erklärt einen subtilen Aspekt des Angriffs: Während der Vorbereitungsphase (Phase 1) vermied der Angreifer bewusst, Liquidität für WOETH und mETH hinzuzufügen. Wenn diese Raten während add_liquidity() aktualisiert worden wären, gäbe es keine Raten-Diskrepanz, und update_rates() würde in diesem Schritt _calc_supply() nicht auslösen.

5. Assets abziehen durch remove_liquidity()

Am Ende jedes Zyklus zieht der Angreifer Assets über remove_liquidity() ab.

Wie der Gewinn erzielt wird

Der Gewinnmechanismus funktioniert wie folgt: In Schritt 1 zahlt der Angreifer LSTs ein und erhält überprägte yETH (wegen des verfälschten Produkts). In Schritt 4, wenn das Angebot korrigiert wird, werden die überschüssigen yETH aus der POL (Staking-Vertrag) verbrannt, nicht aus den Beständen des Angreifers. In Schritt 5 zieht der Angreifer LSTs proportional zu seinen yETH-Beständen ab. Da die POL die Verbrennung aufnahm, während das yETH-Guthaben des Angreifers intakt blieb, zieht der Angreifer am Ende mehr LSTs ab, als er eingezahlt hat. Diese Differenz, die über drei Zyklen erzielt wurde, summiert sich auf ca. 8,1 Mio. US-Dollar.

Zweck des Rebase

Die Aufzeichnung (zwischen dem ersten und dem zweiten Zyklus) zeigt auch einen Aufruf von OETHVaultProxy.rebase(), der einen OETH-Rebase auslöst: Der vom WOETH-Vertrag gehaltene OETH-Saldo erhöht sich, wodurch der effektive Wechselkurs von WOETH steigt. Diese "gerettete" Raten-Diskrepanz ist das, was Schritt 4 des zweiten Zyklus erneut ermöglicht: Wenn update_rates() schließlich aufgerufen wird, erkennt es die Diskrepanz und löst _calc_supply() aus.

Leeren auf Null

Nachdem dieser Fünf-Schritte-Zyklus dreimal wiederholt wurde, hat der Angreifer das Gesamtangebot des Pools unter den Betrag von yETH reduziert, den er hält. Ein letzter Aufruf von remove_liquidity() mit dem verbleibenden Angebot leert es auf NULL.

Der Pool enthält nun null Angebot, null Produkt und null vb_sum. Dieser degenerierte Zustand verletzt die implizite Designannahme, dass ein Pool mit vorherigen Einzahlungen niemals in seinen uninitialisierten Zustand zurückkehren würde.

0x3.3 Phase 3: Ausnutzen von Null-Angebot für zusätzlichen Gewinn (ca. 0,9 Mio. US-Dollar)

Ziel: Eine enorme Menge yETH aus dem degenerierten Poolzustand prägen und dann gegen reale Assets tauschen. Diese Phase nutzt die abhängige Kombination der sekundären Schwachstelle (nicht deaktivierter Bootstrap-Pfad) und Fehlermodus B (Unterlauf) aus, die zusammen ca. 10% der Gesamtverluste ausmachen.

1. Prägen durch Unterlauf

Bei einem Gesamtangebot von Null ruft der Angreifer add_liquidity() mit Staubbeträgen auf (Saldo [1, 1, 1, 1, 1, 1, 1, 9]).

Da prev_supply == 0, tritt der Code in den Bootstrap-Pfad ein, der in Abschnitt 0x2 (Hauptursachenanalyse) beschrieben ist: Er umgeht gespeicherte Zustände und berechnet vb_prod und vb_sum von Grund auf neu über _calc_vb_prod_sum(), gibt diese dann an _calc_supply() weiter. Dies ist die zweite Schwachstelle in Aktion: Der Angreifer hat den Pool in seinen uninitialisierten Zustand zurückversetzt und die Anfangsbedingungen kontrolliert, die an den Löser übergeben werden.

Bei allen virtuellen Salden auf Staubniveau (Wechselkurse nahe 1e18) sind die berechneten Werte:

• vb_sum = 16
• vb_prod ≈ 9,13e20
• _supply = vb_sum = 16

Innerhalb von _calc_supply() werden die Variablen initialisiert als:

• l = _amplification * _vb_sum ≈ 4,5e20 × 16 ≈ 7,2e21
• d = _amplification - PRECISION ≈ 4,49e20
• s = _supply = 16
• r = _vb_prod ≈ 9,13e20

Nun die Subtraktion l - s * r:

$$7.2\times {10}^{21}-16\times 9.13\times {10}^{20}=7.2\times {10}^{21}-1.46\times {10}^{22}\approx -7.4\times {10}^{21}7.2\; \backslash times\; 10^\{21\}\; -\; 16\; \backslash times\; 9.13\; \backslash times\; 10^\{20\}\; =\; 7.2\; \backslash times\; 10^\{21\}\; -\; 1.46\; \backslash times\; 10^\{22\}\; \backslash approx\; -7.4\; \backslash times\; 10^\{21\}$$

Dies ist negativ. In ungeprüfter uint256-Arithmetik wickelt unsafe_sub dies auf einen annähernd riesigen Wert von ca. $2^{256}-7.4\times {10}^{21}2^\{256\}\; -\; 7.4\; \backslash times\; 10^\{21\}$ um. Nach der Division durch d (≈4,49e20) beträgt die resultierende Angebotsschätzung ~2,35e56, und das Protokoll prägt diese gesamte Menge für den Angreifer. Dieser Unterlauf ist nur möglich, weil das Gesamtangebot in Phase 2 auf Null reduziert wurde; unter jedem nicht-degenerierten Poolzustand gilt l > s * r, und die Subtraktion ist sicher.

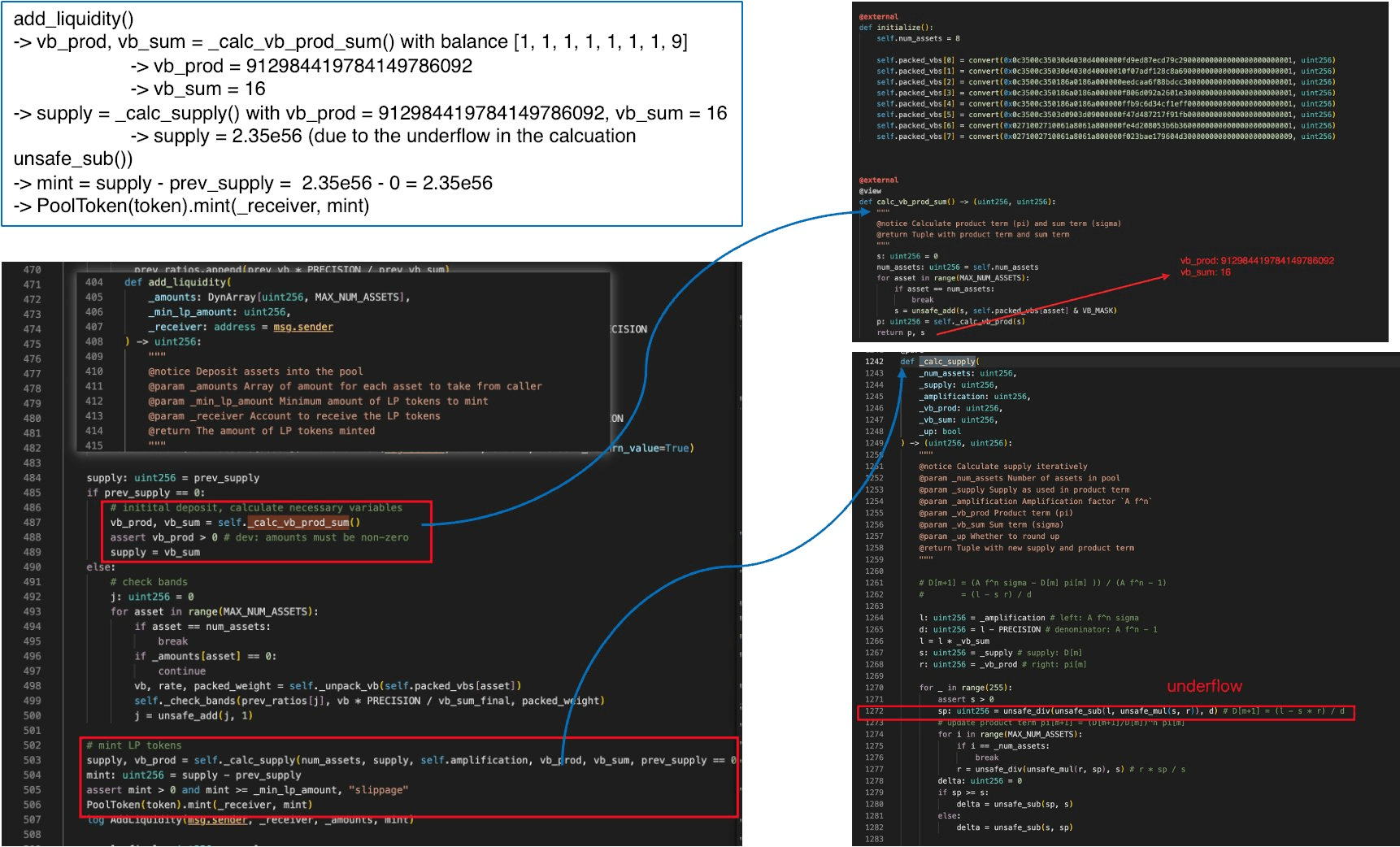
2. Tausch gegen reale Assets

Der Angreifer tauscht einen Teil des überprägten yETH gegen ca. 1.097e18 WETH im yETH-WETH Curve Pool und leert damit dessen WETH-Reserven. Nach Abzug der in Phase 1 ausgegebenen 800e18 WETH betrug der Nettogewinn ca. 0,9 Mio. US-Dollar.

In Kombination mit den ca. 8,1 Mio. US-Dollar an LST-Assets, die während Phase 2 entnommen wurden, erzielte der Angreifer insgesamt einen Gewinn von etwa 9 Millionen US-Dollar, nachdem die Flash-Loans zurückgezahlt wurden.

Eine detaillierte Analyse der Geldflüsse, einschließlich der Herkunft der Gelder und der Zieladressen, wurde in anderen veröffentlichten Analysen (z.B. [2]) behandelt und liegt außerhalb des Umfangs dieses Artikels.

0x4 Missverständnisse korrigiert

Die meisten veröffentlichten Analysen dieses Vorfalls konzentrieren sich auf die arithmetischen Symptome, ohne vollständig zu erklären, wie der Angreifer die Voraussetzungen schafft. Zwei spezifische Behauptungen verdienen eine Korrektur.

0x4.1 Behauptung: "Rundungsinkongruenz zwischen pow_up() und pow_down() verfälscht die Invariante"

Eine gängige Interpretation führt die Hauptursache auf die Verwendung von pow_up() in einigen Code-Pfaden und pow_down() in anderen zurück und argumentiert, dass die richtungsabhängige Inkongruenz ausnutzbare Inkonsistenzen einführt.

Wir haben dies direkt getestet: Wir haben den Vertrag modifiziert, um einheitlich pow_down() zu verwenden (alle pow_up()-Aufrufe ersetzt) und die gesamte Angriffssimulation in Foundry neu ausgeführt. Der Exploit war identisch erfolgreich. Das Produkt kollabiert immer noch auf Null, das Angebot wird immer noch geleert, und der Unterlauf erzeugt immer noch eine aufgeblähte Prägung.

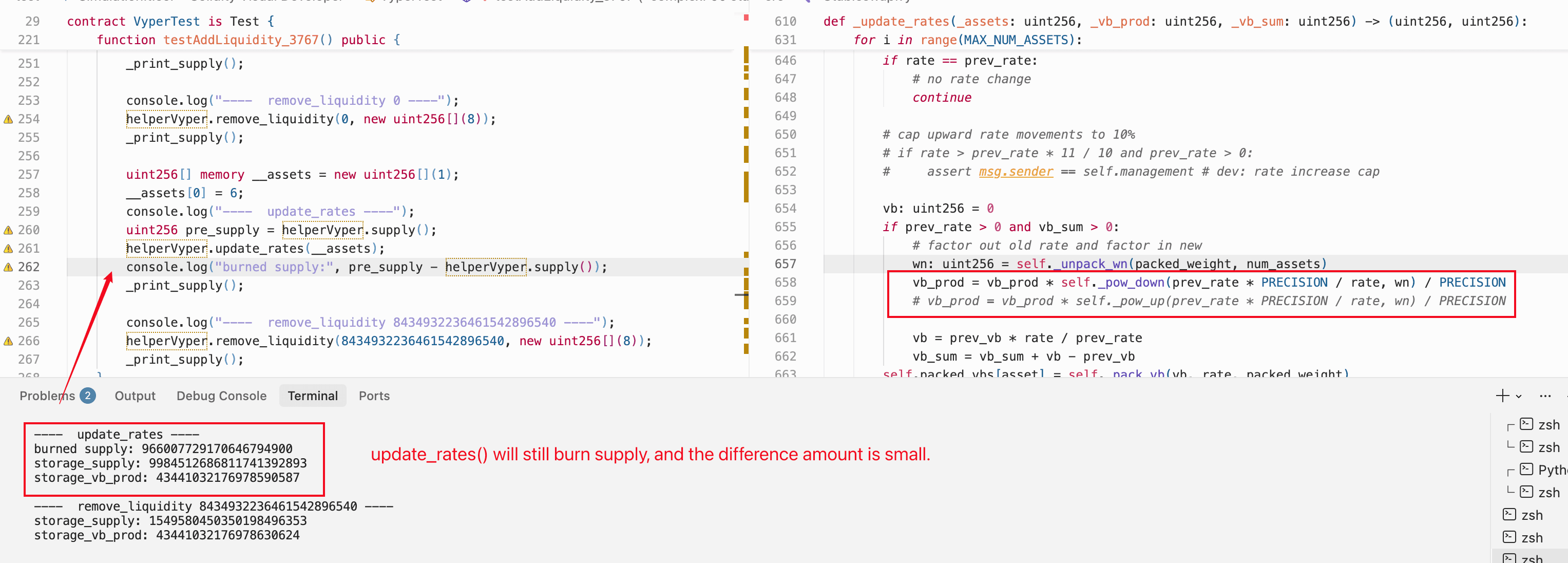
Die Rundung, die den Null-Produktzustand ermöglicht, ist die Ganzzahl-Division in r = unsafe_div(unsafe_mul(r, sp), s) innerhalb der Iterationsschleife, nicht die Richtung der Rundung in den Potenzfunktionen, die zur Schätzung der anfänglichen Produktwerte verwendet werden.

0x4.2 Behauptung: "Unterlauf in der zweiten Iteration setzt den Zwischenterm auf Null"

Eine weit verbreitete Erklärung besagt, dass während der zweiten Iteration von _calc_supply() ein Unterlauf in unsafe_sub sp ≈ 1,94e18 erzeugt, was dann dazu führt, dass r auf Null abgerundet wird.

Wir haben die exakten Zwischenwerte sowohl mit Foundry (On-Chain-Wiederholung) als auch mit Python (mathematische Verifizierung) reproduziert. Die Foundry-Simulation verfolgt _calc_supply() Iteration für Iteration:

======= _calc_supply iteration 0 =======
  l = 4905875511098192451202650000000000000000
  s = 2514373972590845290489        ← anfängliches Angebot
  r = 3538247433646816               ← anfängliches Produkt (sehr klein)
  d = 4490000000000000000000

  sp = (l - s*r) / d ≈ 1.093e22     ← neues Angebot springt ~4x
  new r ≈ 4.49e22                    ← Produkt bläht sich drastisch auf

======= _calc_supply iteration 1 =======
  s = 10926206313726454855296        ← vom vorherigen sp
  r = 44892226765713223838396        ← von der vorherigen inneren Schleife

  sp = 19113493328251743069          ← ≈ 1,91e19, legitim klein
  new r = 0                          ← rundet auf Null!

Die entscheidende Beobachtung: In Iteration 1 ergibt sich sp zu ca. 1,91e19. Dies ist ein legitim kleiner positiver Wert, kein Artefakt eines Unterlaufs. Die Subtraktion l - s*r ergibt ein kleines positives Ergebnis, da die verstärkungs-gewichtete Summe l und der Angebot-Produkt-Term s*r in dieser Iteration nahe beieinander liegen.

Was das Produkt auf Null setzt, ist, was danach geschieht: Die innere Schleife berechnet r = r * sp / s, wobei sp (≈1,91e19) weitaus kleiner ist als s (≈1,09e22). Der Zähler r * sp fällt unter den Nenner s, und die Ganzzahl-Division schneidet das Ergebnis auf Null.

Wir haben dies unabhängig in Python verifiziert, indem wir die gleichen Werte mit beliebig präzisen ganzen Zahlen berechnet und bestätigt haben, dass die Subtraktion keinen Unterlauf verursacht:

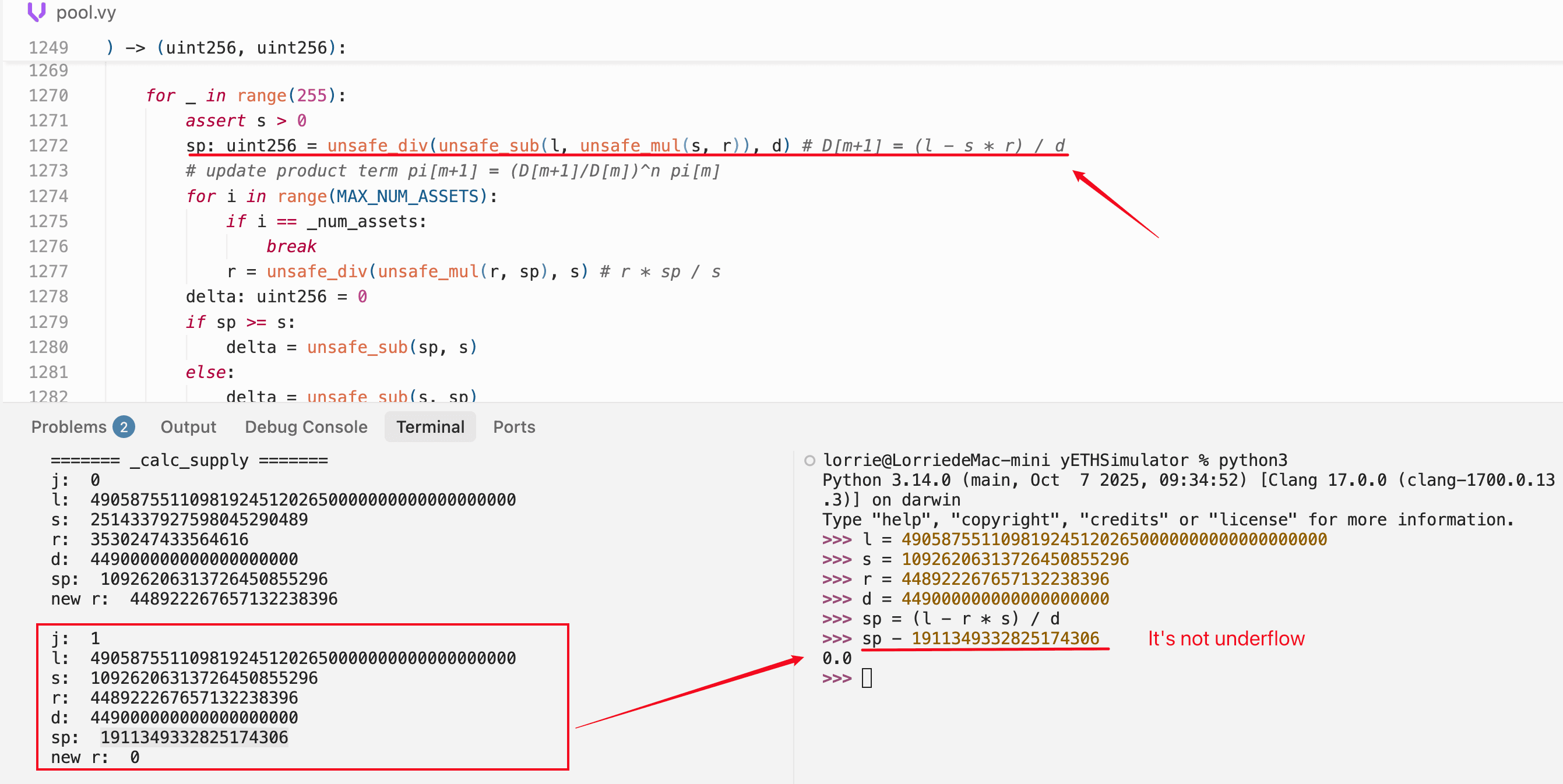
Das Produkt setzt sich durch Rundung bei der Division auf Null, nicht durch Unterlauf bei der Subtraktion. Der unsafe_sub-Unterlauf, der das Angebot aufbläht, tritt in einem völlig anderen Kontext auf: Phase 3 des Angriffs, wenn Staub-Liquidität zu einem Pool hinzugefügt wird, der auf Null Angebot geleert wurde.

0x5 Fazit

Der yETH-Exploit umfasste zwei Schwachstellen mit asymmetrischem Einfluss. Unsichere Arithmetik in _calc_supply() war die primäre Hauptursache: Ihr Abrundungsfehler (Fehlermodus A) ermöglichte unabhängig davon Verluste von ca. 8,1 Mio. US-Dollar allein durch Phase 2. Der nicht deaktivierte Bootstrap-Pfad war eine sekundäre Schwachstelle; in Kombination mit dem Unterlauffehler (Fehlermodus B) ermöglichte er zusätzliche ca. 0,9 Mio. US-Dollar in Phase 3, aber erst, nachdem Phase 2 das Angebot bereits auf Null reduziert hatte. Diese Verlustaufschlüsselung unterscheidet die vorliegende Analyse von anderen veröffentlichten Berichten, die Gewinne aus Phase 2 und Phase 3 nicht trennen.

Der offizielle Post-Mortem [2] identifiziert fünf Hauptursachen. Wir stufen diese neu als zwei Mängel (unsichere Arithmetik konsolidiert offizielle #1 und #5; nicht deaktivierter Bootstrap-Pfad als #4) und zwei architektonische Vorbedingungen (#2 asymmetrische Π-Behandlung; #3 POL-fähiger Null-Angebot-Zustand) ein. Der Unterschied: Mängel sind Implementierungsfehler, die die Designabsicht verletzen (der Löser sollte keine Null-Produkte erzeugen oder unterlaufen), während Vorbedingungen Designentscheidungen sind, die als beabsichtigt funktionieren, aber eine ausnutzbare Angriffsfläche schaffen, wenn sie mit Mängeln kombiniert werden.

Empfehlungen

• Geprüfte Arithmetik in Invariantenlösungern. Verwenden Sie safe_div und safe_sub mit explizitem Rückruf bei Unterlauf/Überlauf, auch auf Kosten der Gaseffizienz. Der Löser läuft höchstens 256 Iterationen, und der Gasaufwand ist vernachlässigbar im Vergleich zum Sicherheitsrisiko.
• Grenzprüfungen für Zwischenwerte. Validieren Sie, dass der Produktterm zwischen den Iterationen in einem sinnvollen Bereich bleibt. Ein Produkt, das auf Null fällt, oder eine Angebotsschätzung, die zwischen den Iterationen um Größenordnungen steigt, signalisiert einen degenerierten Zustand.
• Grenzen für Ungleichgewichte. Erzwingen Sie maximale Abweichungen zwischen dem virtuellen Saldo eines beliebigen Assets und seinem zielproportionalen Saldo. Dies würde verhindern, dass Phase 1 die Voraussetzungen schafft.
• Prüfung der Invarianten-Monotonie. Nach der Rückgabe von _calc_supply() überprüfen Sie, ob das neue Angebot mit der Änderungsrichtung konsistent ist (Liquiditätshinzufügung sollte das Angebot niemals verringern, Ratenaktualisierungen sollten keine 10-fachen Änderungen ergeben usw.).
• Dauerhaftes Deaktivieren von Initialisierungspfaden. Nach der ersten Einzahlung des Pools sperren Sie den Bootstrap-Zweig prev_supply == 0 so, dass er nicht erneut aufgerufen werden kann. Dies würde Phase 3 vollständig verhindern.
• Verhindern von Null-Angebot-Zuständen. Stellen Sie sicher, dass protokollweite Verbrennungen (von POL oder Staking-Verträgen) nicht die Gesamtversorgung auf Null reduzieren können, während der Pool Nicht-Null-Salden hält. Eine minimale Angebotsuntergrenze würde den Übergang in den degenerierten Zustand blockieren, der die Wiederholung des Bootstraps ermöglicht.
• Echtzeit-Anomalieerkennung. Überwachen Sie abnormale Zustandsübergänge (wie das Fallen von Produkttermen auf Null, das Ansteigen des Angebots um Größenordnungen oder wiederholte Hinzufüge-/Entnahmezyklen in kurzen Zeiträumen) und lösen Sie Warnungen oder Notabschaltungen aus, bevor sich Verluste häufen.

Referenzen

1. Yearn Finance Vorankündigung des Vorfalls
2. Yearn Security Post-Mortem
3. yETH Dokumentation
4. yETH Whitepaper: Ableitung der Invariante
5. Angriffstransaktion im BlockSec Explorer
6. BlockSec: Analyse des Balancer Boosted Pool Vorfalls (August 2023)

Über BlockSec

BlockSec ist ein Full-Stack-Anbieter für Blockchain-Sicherheit und Krypto-Compliance. Wir entwickeln Produkte und Dienstleistungen, die Kunden bei der Durchführung von Code-Audits (einschließlich Smart Contracts, Blockchain und Wallets), der Echtzeit-Abwehr von Angriffen, der Analyse von Vorfällen, der Verfolgung von illegalen Geldern und der Erfüllung von AML/CFT-Verpflichtungen über den gesamten Lebenszyklus von Protokollen und Plattformen hinweg unterstützen.

BlockSec hat mehrere Blockchain-Sicherheitsartikel auf renommierten Konferenzen veröffentlicht, mehrere Zero-Day-Angriffe von DeFi-Anwendungen gemeldet, mehrere Hackerangriffe blockiert, um mehr als 20 Millionen Dollar zu retten, und Milliarden von Kryptowährungen gesichert.

• Offizielle Website: https://blocksec.com/

• Offizieller Twitter-Account: https://twitter.com/BlockSecTeam

• 🔗 BlockSec Audit Service : Anfrage einreichen

• 🔗 Phalcon Security APP: Demo buchen

• 🔗 Phalcon Compliance