#10 Panoptisches Ereignis: XOR-Linearität bricht Positions-Fingerabdruck-Schema

Am 25. August 2025 führte Panoptic mit Unterstützung von Cantina und Seal911 eine White-Hat-Rettungsaktion durch und sicherte etwa 400.000 US-Dollar an gefährdeten Geldern [1]. Die Grundursache war ein Fehler in der Konstruktion von s_positionsHash: Das Protokoll verwendete XOR, um Keccak256-Hashes von Positions-IDs zu einem einzigen Fingerabdruck zu aggregieren. Während einzelne Keccak256-Hashes kollisionsresistent bleiben, macht die mathematische Linearität von XOR den zusammengesetzten Fingerabdruck unsicher. Ein Angreifer kann eine Reihe gefälschter Positions-IDs generieren, deren XOR-aggregierter Hash mit jedem Ziel-Fingerabdruck übereinstimmt, wodurch die Positionsprüfung des Protokolls umgangen und Sicherheiten abgezogen werden, ohne Schulden zurückzuzahlen.

Hintergrund

Panoptic ist ein dezentralisiertes Protokoll für den Handel mit ewigen Optionen, das auf Ethereum aufgebaut ist und es Benutzern ermöglicht, Put- und Call-Optionen zu handeln.

Die Funktion withdraw() hat einen Eingabeparameter positionList, der aus einer Menge von tokenIds besteht. Jede tokenId repräsentiert eine Position. Die Funktion withdraw() prüft den Schuldenstatus jeder Position basierend auf s_positionsHash und ruft dann die Sicherheiten des Benutzers ab.

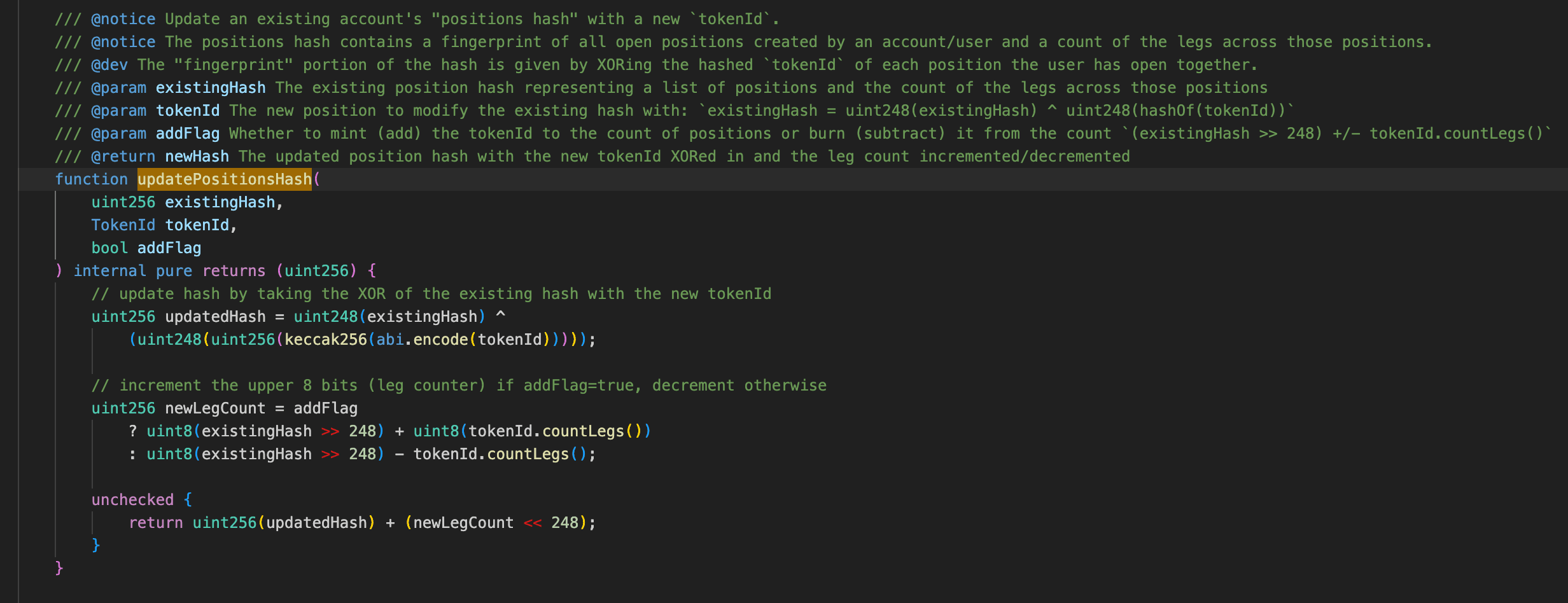
Um Gas zu sparen, speichert das Protokoll nicht jede Position (d. h. tokenId) des Benutzers. Stattdessen berechnet es einen Fingerabdruck basierend auf allen tokenIds des Benutzers und zeichnet ihn in s_positionsHash auf. Die 8 höchstwertigen Bits jedes s_positionsHash repräsentieren numLegs, während die unteren 248 Bits den user position hash repräsentieren.

Für jede übergebene tokenId berechnet das Protokoll deren Hash, nimmt die unteren 248 Bits und aktualisiert den user position hash, indem es einen bitweisen XOR mit den unteren 248 Bits des aktuellen s_positionsHash durchführt.

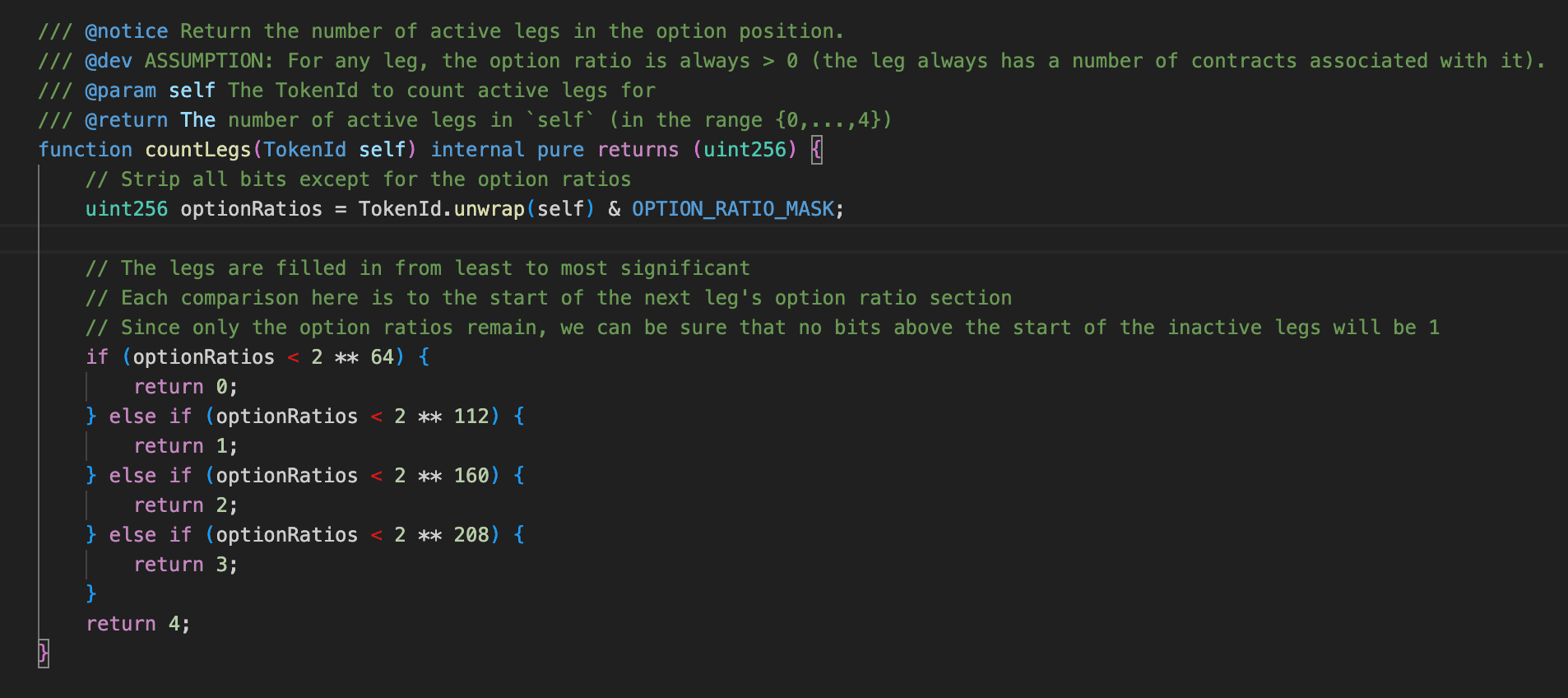
Gleichzeitig wird countLegs basierend auf dem numerischen Bereich der tokenId angepasst: Es bleibt unverändert, wenn tokenId kleiner als $2^{64}2^\{64\}$ ist, und erhöht sich um 1, 2 oder 3, wenn es in den Bereichen $(2^{64},2^{112})(2^\{64\},\; 2^\{112\})$, $(2^{112},2^{168})(2^\{112\},\; 2^\{168\})$ bzw. $(2^{168},2^{208})(2^\{168\},\; 2^\{208\})$ liegt. Dies wird schließlich in die obersten 8 Bits von s_positionsHash geschrieben, um numLegs zu aktualisieren.

Schwachstellenanalyse

Die Grundursache ist ein Fehler im Algorithmus des Vertrags zur Konstruktion von s_positionsHash, insbesondere die Verwendung der XOR-Operation zur Aggregation von Keccak256-Hash-Ergebnissen. Während eine einzelne Hash-Funktion sicher bleibt, macht die mathematische Linearität der XOR-Operation den gesamten Fingerabdruck-Algorithmus (d. h. die XOR-Summe von Hashes) unsicher [2].

Linearität impliziert, dass ein Angreifer die Hash-Funktion selbst nicht brechen muss (d. h. die tokenId aus dem Hash umkehren). Stattdessen können sie eine kombinatorische Strategie anwenden: Generieren einer großen Anzahl von zufälligen tokenIds, Berechnen ihres Keccak256(tokenId) und aus diesen Hash-Werten eine bestimmte Teilmenge auswählen, sodass die XOR-Summe dieser tokenId-Hashes exakt dem Ziel-Fingerabdruck des Opfers entspricht.

Dies ermöglicht es einem Angreifer, bei Aufruf von withdraw() eine Reihe gefälschter tokenIds zu übergeben, um den Gesundheitstest zu bestehen und alle Sicherheiten im Zusammenhang mit s_positionsHash abzurufen.

Theorie

Nehmen wir an, der Positionsfingerabdruck des Benutzers s_positionsHash hat einen user position hash von $TT$ und numLegs von $kk$, mit Benutzer tokenIds $\{t_1,t_2,\dots ,t_n\}\backslash \{t\_1,\; t\_2,\; \backslash dots,\; t\_n\backslash \}$. Somit gilt:

$$\underset{i=1}{\overset{k}{⨁}}[\text{Hash}(t_i)(\mathrm{m}\mathrm{o}\mathrm{d}{2}^{248})]=T\backslash bigoplus\_\{i=1\}^\{k\}\; [\backslash text\{Hash\}(t\_i)\; \backslash pmod\{2^\{248\}\}]\; =\; T$$

Hier kann jeder 248-Bit-Hash-Wert als 248-dimensionaler Vektor betrachtet werden.

$$\text{Hash}(t_i)(\mathrm{m}\mathrm{o}\mathrm{d}{2}^{248})=[b_0,b_1,\dots ,b_{247}{]}^T,wobei{b}_i\in \{0,1\}\backslash text\{Hash\}(t\_i)\; \backslash pmod\{2^\{248\}\}\; =\; [b\_0,\; b\_1,\; \backslash dots,\; b\_\{247\}]^T,\; wobei\backslash \; b\_i\; \backslash in\; \backslash \{0,\; 1\backslash \}$$

Daher liegt $TT$ in einem 248-dimensionalen Raum aus 0en und 1en (${\mathbb{F}}_2^{248}\backslash mathbb\{F\}\_2^\{248\}$). In diesem Raum ist die XOR-Operation gleich der Vektoraddition (Anhang I).

Das Ziel des Angreifers ist es, $nn$ 248-dimensionale Vektoren $\{v_1,v_2,\dots ,v_n\}\backslash \{v\_1,\; v\_2,\; \backslash dots,\; v\_n\backslash \}$ aus allen verfügbaren Vektoren zu finden, sodass die unteren 248 Bits ihrer XOR-Summe gleich $TT$ sind. Somit können wir das Ziel des Angreifers als System linearer Gleichungen formulieren:

$$x_1{v}_1+x_2{v}_2+\cdots +x_n{v}_n=Tx\_1\; v\_1\; +\; x\_2\; v\_2\; +\; \backslash dots\; +\; x\_n\; v\_n\; =\; T$$

Insbesondere müssen wir $TT$ nicht direkt konstruieren. Stattdessen wählen wir $nn$ linear unabhängige Hash-Vektoren $\{v_1,v_2,\dots ,v_n\}\backslash \{v\_1,\; v\_2,\; \backslash dots,\; v\_n\backslash \}$ (wobei $nn$ der Dimension 248 entspricht) und verwenden sie als Spaltenvektoren, um eine $n\times nn\; \backslash times\; n$ Matrix $AA$ zu konstruieren:

$$A=[v_1,v_2,\dots ,v_n]A\; =\; [v\_1,\; v\_2,\; \backslash dots,\; v\_n]$$

Das Problem verwandelt sich dann in die Suche nach einem Koeffizientenvektor $xx$, so dass:

$$A\cdot x=TA\; \backslash cdot\; x\; =\; T$$

Wobei $x=[x_1,x_2,\dots ,x_n{]}^{T}x\; =\; [x\_1,\; x\_2,\; \backslash dots,\; x\_n]^T$ und $x_i\in \{0,1\}x\_i\; \backslash in\; \backslash \{0,\; 1\backslash \}$.

Gemäß der linearen Algebra erstreckt sich die Matrix $AA$, solange sie vollen Rang hat, über den gesamten $nn$-dimensionalen Raum. Das bedeutet, dass für jedes Ziel $TT$ das Gleichungssystem eine eindeutige Lösung hat. Nach der Lösung von $xx$ behalten wir einfach diejenigen Vektoren $v_{i}v\_i$ bei, für die $x_i=1x\_i=1$; ihre XOR-Summe ist $TT$.

Beispiel

Zur besseren Verständlichkeit demonstrieren wir diesen Konstruktionsprozess anhand einer Fallstudie. Nehmen wir an, die Vektoren sind 3-dimensional, jede Dimension besteht nur aus 0 oder 1, und der Ziel-Hashwert ist 101, d. h. $T=[1,0,1{]}^{T}T\; =\; [1,\; 0,\; 1]^T$.

Als Nächstes generieren wir zufällig 3 Hash-Werte:

• $v_1=[1,1,0{]}^{T}v\_1\; =\; [1,\; 1,\; 0]^T$
• $v_2=[0,1,0{]}^{T}v\_2\; =\; [0,\; 1,\; 0]^T$
• $v_3=[0,1,1{]}^{T}v\_3\; =\; [0,\; 1,\; 1]^T$

Wir konstruieren die Matrix $AA$ mit diesen drei Vektoren als Spalten und stellen die Gleichung $Ax=TAx=T$ auf:

Durch Gaußsche Elimination erhalten wir $x=[1,0,1{]}^{T}x\; =\; [1,\; 0,\; 1]^T$. Das bedeutet, wir müssen $v_{1}v\_1$ und $v_{3}v\_3$ auswählen (entsprechend $x_1=1,x_3=1x\_1=1,\; x\_3=1$), und ihre XOR-Summe entspricht exakt $TT$.

Auswahl von n linear unabhängigen Vektoren

Wie bereits erwähnt, müssen wir zur Lösung von $Ax=TAx=T$ eine Matrix $AA$ mit vollem Rang konstruieren. Da wir es mit einem extrem großen Vektorraum ($m=2^{248}m\; =\; 2^\{248\}$) zu tun haben, stellt sich die Kernfrage: Wie wählen wir schnell $nn$ linear unabhängige Vektoren aus diesem riesigen Raum aus?

Betrachten wir die einfachste Methode: zufälliges Generieren von $nn$ tokenIds und Auswählen ihrer Hash-Ergebnisse als Vektoren.

Über ${\mathbb{F}}_2\backslash mathbb\{F\}\_2$ ist die Wahrscheinlichkeit $PP$, dass $nn$ zufällig ausgewählte $nn$-dimensionale Vektoren eine vollen Rangmatrix bilden:

$$P(n)=\prod _{k=0}^{n-1}(1-\frac{2^k}{2^n})P(n)\; =\; \backslash prod\_\{k=0\}^\{n-1\}\; \backslash left(1\; -\; \backslash frac\{2^k\}\{2^n\}\backslash right)$$

Wenn $nn$ groß ist (in diesem Beispiel $n=248n=248$), konvergiert diese Wahrscheinlichkeit gegen eine Konstante (Anhang II):

$$\underset{n\to \mathrm{\infty }}{\lim }P(n)\approx 0.28879\backslash lim\_\{n\; \backslash to\; \backslash infty\}\; P(n)\; \backslash approx\; 0.28879$$

Das bedeutet, jeder zufällige Versuch hat eine Erfolgswahrscheinlichkeit von etwa 28,9 %. Im Durchschnitt benötigt ein Angreifer nur etwa 3,5 Versuche, um eine Menge linear unabhängiger Vektoren zu finden. Daher sind die Rechenkosten extrem niedrig, und der Angreifer kann schnell eine Matrix $AA$ konstruieren, die die Bedingungen erfüllt.

Um countLegs in den obersten 8 Bits zu steuern, müssen wir nur den Bereich der zufällig generierten tokenId-Werte basierend auf dem Ziel countLegs anpassen.

Wenn wir zum Beispiel möchten, dass die numLegs im gefälschten Fingerabdruck 0 sind, stellen wir einfach sicher, dass die $nn$ zufällig generierten tokenIds alle kleiner als $2^{64}2^\{64\}$ sind. Da die Bein-Inkremente für tokenIds in diesem Bereich 0 betragen, wird die endgültige akkumulierte numLegs unweigerlich 0 sein, unabhängig davon, welche Vektoren die Gaußsche Eliminationslösung $xx$ auswählt.

Angriffsanalyse

Der White-Hat-Retter initiierte mehrere Rettungstransaktionen. Der Einfachheit halber basiert die folgende Diskussion auf nur einer dieser Transaktionen [3].

Die Kernlogik besteht aus den folgenden 5 Schritten:

1. Leihen Sie 0,23e8 WBTC und 28e18 WETH über einen Flash-Loan von Aave.
2. Zahlen Sie 0,23e8 WBTC und 28e18 WETH in den poWBTC-Vertrag und den 0x1f8d_poWETH-Vertrag ein.
3. Rufen Sie mintOptions() des PanopticPool-Vertrags mit einer normalen positionIdList auf, um Gelder zu leihen und eine gehebelte Position zu eröffnen.
4. Rufen Sie withdraw() mit den gefälschten tokenIds auf. Da diese gefälschten Positionen eine positionSize von 0 haben, gibt die Funktion tokenRequired als 0 zurück, was bedeutet, dass die erforderlichen Gesamtsicherheiten für alle Positionen fälschlicherweise als null berechnet werden. In der Zwischenzeit ist der von diesen tokenIds generierte s_positionsHash exakt derselbe wie der in Schritt 3 generierte, was es dem Retter ermöglicht, alle Sicherheiten abzurufen, ohne Schulden zurückzuzahlen.
5. Zahlen Sie den Flash-Loan zurück und führen Sie die nächste Runde aus.

Zusammenfassung

Dieser Vorfall hebt zwei sich verstärkende Mängel hervor, die zusammen den unbefugten Abzug von Sicherheiten ermöglichten.

• XOR ist keine sichere Aggregationsfunktion für Hashes. Keccak256 ist kollisionsresistent, aber die Linearität von XOR bedeutet, dass die XOR-Summe mehrerer Hashes diese Eigenschaft nicht erbt. Die Konstruktion einer Menge von Eingaben, deren Hashes zu jedem Zielwert XORen, reduziert sich auf die Lösung eines Systems linearer Gleichungen über ${\mathbb{F}}_2\backslash mathbb\{F\}\_2$, was rechnerisch trivial ist. Hash-Zusammensetzung erfordert Operationen, die die Kollisionsresistenz beibehalten, wie z. B. Verkettung gefolgt von erneuter Hashing.
• Fehlende Validierung von Positions-IDs. Das Protokoll prüfte nicht, ob die übergebenen positionIds gültigen Optionspositionen entsprachen. Werte unter $2^{64}2^\{64\}$ haben ein countLegs von 0 und eine positionSize von 0, was bedeutet, dass die gefälschten Positionen keine Schulden verursachen. Dies ermöglichte es dem Angreifer, den Gesundheitstest mit null erforderlichen Sicherheiten zu bestehen und gleichzeitig den Ziel-Fingerabdruck abzugleichen.

Referenz

1. https://x.com/Panoptic_xyz/status/1961187739866644524

2. https://cseweb.ucsd.edu/~mihir/papers/inchash.pdf

3. https://app.blocksec.com/explorer/tx/eth/0x67a45dfe5ff4b190058674d7c791bbdc48e889f319f937c24fa13a5f9093f088

Anhang

Die folgenden beiden Anhänge liefern eine mathematische Erklärung und einen Beweis für die Aussagen im Haupttext, nämlich dass die XOR-Operation der Vektoraddition entspricht (Anhang I) und die Wahrscheinlichkeit, dass eine zufällige Matrix vollen Rang hat (Anhang II).

Anhang I

Im endlichen Körper ${\mathbb{F}}_2=\{0,1\}\backslash mathbb\{F\}\_2\; =\; \backslash \{0,\; 1\backslash \}$ ist die Addition als Addition modulo 2 definiert:

Die Beobachtung zeigt, dass dies identisch mit der logischen Operation Exclusive OR (XOR, Symbol $\oplus \backslash oplus$) ist.

Für den $nn$-dimensionalen Vektorraum ${\mathbb{F}}_2^n\backslash mathbb\{F\}\_2^n$ (in diesem Fall $n=248n=248$) ist die Addition zweier Vektoren $u=[u_1,\dots ,u_n{]}^{T}u\; =\; [u\_1,\; \backslash dots,\; u\_n]^T$ und $v=[v_1,\dots ,v_n{]}^{T}v\; =\; [v\_1,\; \backslash dots,\; v\_n]^T$ als komponentenweise Addition modulo 2 definiert:

$$u+v=\left[\begin{array}{c}{u}_1+v_1(\mathrm{m}\mathrm{o}\mathrm{d}2)\\ \mathrm{⋮}\\ u_n+v_n(\mathrm{m}\mathrm{o}\mathrm{d}2)\end{array}\right]=\left[\begin{array}{c}{u}_1\oplus v_1\\ \mathrm{⋮}\\ u_n\oplus v_n\end{array}\right]=u\oplus vu\; +\; v\; =\; \backslash begin\{bmatrix\}\; u\_1\; +\; v\_1\; \backslash pmod\; 2\; \backslash \backslash \; \backslash vdots\; \backslash \backslash \; u\_n\; +\; v\_n\; \backslash pmod\; 2\; \backslash end\{bmatrix\}\; =\; \backslash begin\{bmatrix\}\; u\_1\; \backslash oplus\; v\_1\; \backslash \backslash \; \backslash vdots\; \backslash \backslash \; u\_n\; \backslash oplus\; v\_n\; \backslash end\{bmatrix\}\; =\; u\; \backslash oplus\; v$$

Daher ist im Vektorraum ${\mathbb{F}}_2^n\backslash mathbb\{F\}\_2^\{n\}$ die Vektoraddition äquivalent zur bitweisen XOR-Operation auf den Vektorkomponenten.

Anhang II

Damit die Matrix vollen Rang hat, müssen diese $nn$ Vektoren linear unabhängig sein.

Der erste Vektor $v_{1}v\_1$ kann jeder Vektor in ${\mathbb{F}}_2^n\backslash mathbb\{F\}\_2^n$ außer dem Nullvektor sein, was $2^n-12^n\; -\; 1$ Optionen bietet; der zweite Vektor $v_{2}v\_2$ darf nicht im von $\{v_1\}\backslash \{v\_1\backslash \}$ aufgespannten Unterraum liegen, der $2^{1}2^1$ Vektoren enthält, was $2^n-22^n\; -\; 2$ Optionen übrig lässt; diesem Logik folgend darf der $kk$-te Vektor $v_{k}v\_k$ nicht im von den vorherigen $k-1k-1$ Vektoren aufgespannten Unterraum liegen, was $2^n-2^{k-1}2^n\; -\; 2^\{k-1\}$ mögliche Optionen ergibt.

Die Gesamtzahl solcher Matrizen (d. h. die Ordnung von $GL(n,{\mathbb{F}}_2)GL(n,\; \backslash mathbb\{F\}\_2)$) ist:

$$N=\prod _{k=0}^{n-1}(2^n-2^k)=(2^n-1)(2^n-2)(2^n-4)\cdots (2^n-2^{n-1})N\; =\; \backslash prod\_\{k=0\}^\{n-1\}\; (2^n\; -\; 2^k)\; =\; (2^n\; -\; 1)(2^n\; -\; 2)(2^n\; -\; 4)\backslash cdots(2^n\; -\; 2^\{n-1\})$$

Und die Gesamtzahl aller möglichen $n\times nn\; \backslash times\; n$ Matrizen beträgt $(2^n{)}^n=2^{n^2}(2^n)^n\; =\; 2^\{n^2\}$.

Daher ist die Wahrscheinlichkeit $PP$:

$$P=\frac{\prod _{k=0}^{n-1}(2^n-2^k)}{2^{n^2}}=\prod _{k=0}^{n-1}\left(\frac{2^n-2^k}{2^n}\right)=\prod _{k=0}^{n-1}(1-\frac{2^k}{2^n})P\; =\; \backslash frac\{\backslash prod\_\{k=0\}^\{n-1\}\; (2^n\; -\; 2^k)\}\{2^\{n^2\}\}\; =\; \backslash prod\_\{k=0\}^\{n-1\}\; \backslash left(\; \backslash frac\{2^n\; -\; 2^k\}\{2^n\}\; \backslash right)\; =\; \backslash prod\_\{k=0\}^\{n-1\}\; (1\; -\; \backslash frac\{2^k\}\{2^n\})$$

Wenn wir $j=n-kj\; =\; n\; -\; k$ setzen, können wir diesen Ausdruck umschreiben als:

$$P=\prod _{j=1}^n(1-\frac{1}{2^j})P\; =\; \backslash prod\_\{j=1\}^\{n\}\; \backslash left(1\; -\; \backslash frac\{1\}\{2^j\}\backslash right)$$

Wenn $n\to \mathrm{\infty }n\; \backslash to\; \backslash infty$, konvergiert dieses Produkt gegen eine Konstante:

$$P\approx 0.288788P\; \backslash approx\; 0.288788$$

Das bedeutet, dass für große $nn$ die Wahrscheinlichkeit, dass eine zufällige Matrix vollen Rang hat, etwa 28,9 % beträgt.

Über BlockSec

BlockSec ist ein Anbieter von Blockchain-Sicherheit und Krypto-Compliance aus einer Hand. Wir entwickeln Produkte und Dienstleistungen, die Kunden bei der Durchführung von Code-Audits (einschließlich Smart Contracts, Blockchain und Wallets), der Echtzeit-Abwehr von Angriffen, der Analyse von Vorfällen, der Rückverfolgung illegaler Gelder und der Erfüllung von AML/CFT-Verpflichtungen über den gesamten Lebenszyklus von Protokollen und Plattformen hinweg unterstützen.

BlockSec hat zahlreiche Blockchain-Sicherheitsarbeiten auf renommierten Konferenzen veröffentlicht, mehrere Zero-Day-Angriffe auf DeFi-Anwendungen gemeldet, mehrere Hacks blockiert, um mehr als 20 Millionen Dollar zu retten, und Kryptowährungen im Wert von mehreren Milliarden Dollar gesichert.

• Offizielle Website: https://blocksec.com/

• Offizielles Twitter-Konto: https://twitter.com/BlockSecTeam

• 🔗 BlockSec Auditing Service : Anfrage senden

• 🔗 Phalcon Security APP: Demo buchen

• 🔗 Phalcon Compliance