#10 Panoptic Incident: XOR Linearity Breaks the Position Fingerprint Scheme

On August 25, 2025, with the assistance of Cantina and Seal911, Panoptic conducted a white hat rescue operation, securing approximately $400K in at-risk funds [1]. The root cause was a flaw in the construction of s_positionsHash: the protocol used XOR to aggregate Keccak256 hashes of position IDs into a single fingerprint. While individual Keccak256 hashes remain collision-resistant, XOR's mathematical linearity makes the composite fingerprint insecure. An attacker can generate a set of forged position IDs whose XOR-aggregated hash matches any target fingerprint, bypassing the protocol's position verification and withdrawing collateral without repaying debt.

Background

Panoptic is a decentralized perpetual options trading protocol built on Ethereum that enables users to trade put and call options.

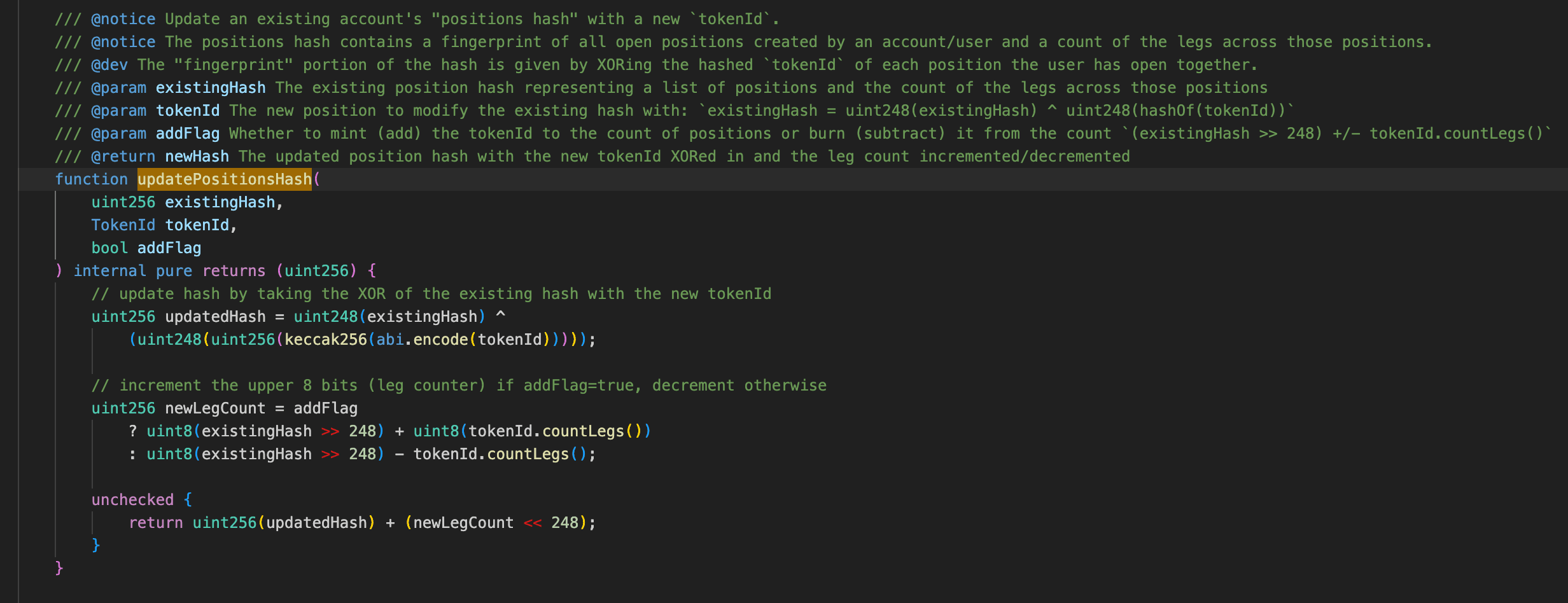
The function withdraw() has an input parameter positionList, which consists of a set of tokenIds. Each tokenId represents a position. The function withdraw() checks the debt status of each position based on s_positionsHash and then retrieves the user's collateral.

To save gas, the protocol does not store every position (i.e., tokenId) of the user. Instead, it calculates a fingerprint based on all the user's tokenIds and records it in s_positionsHash. The most significant 8 bits of each s_positionsHash represent numLegs, while the lower 248 bits represent the user position hash.

For each passed tokenId, the protocol calculates its hash, takes the lower 248 bits, and updates the user position hash by performing a bitwise XOR with the lower 248 bits of the current s_positionsHash.

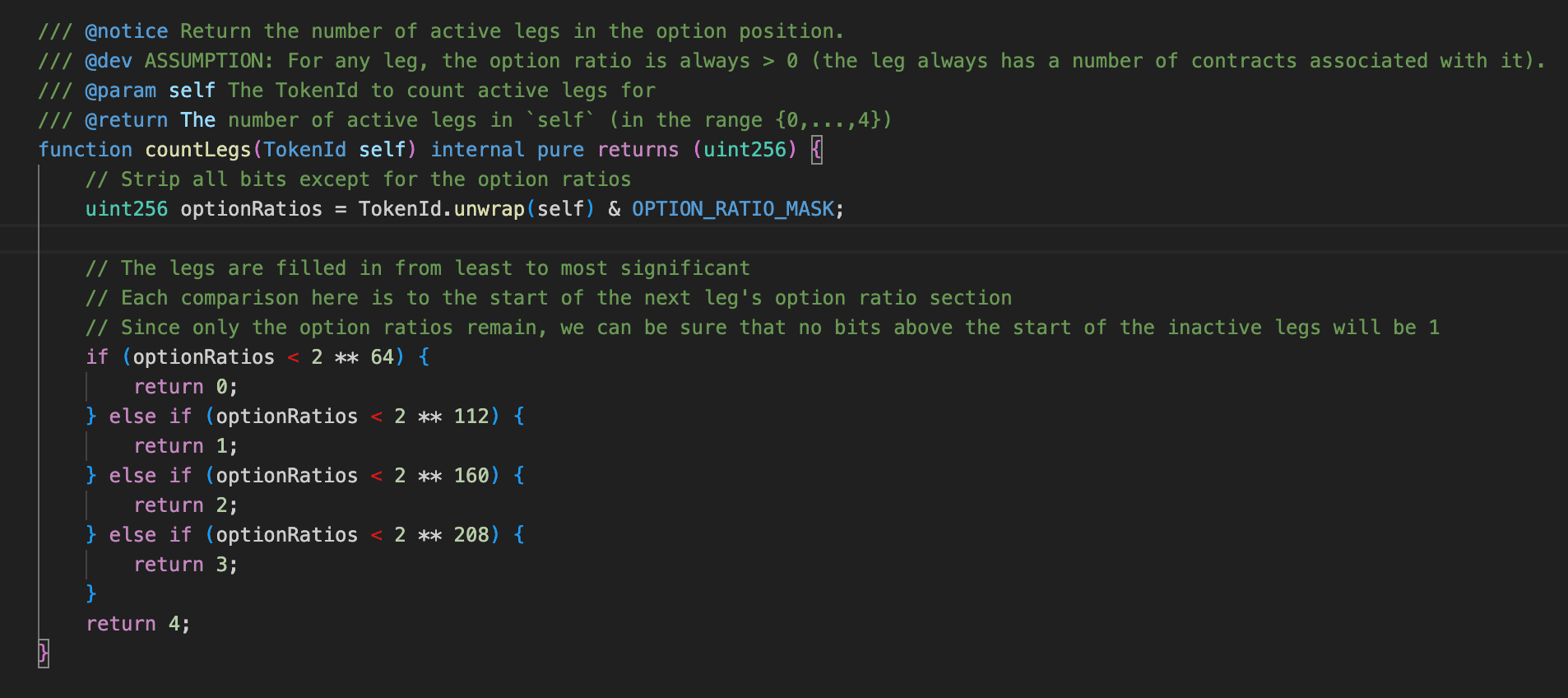
Simultaneously, countLegs is adjusted based on the numerical range of the tokenId: it remains unchanged when tokenId is below $2^{64}2^\{64\}$, and increases by 1, 2, or 3 when in the ranges $(2^{64},2^{112})(2^\{64\},\; 2^\{112\})$, $(2^{112},2^{168})(2^\{112\},\; 2^\{168\})$, and $(2^{168},2^{208})(2^\{168\},\; 2^\{208\})$ respectively. This is finally written to the top 8 bits of s_positionsHash to update numLegs.

Vulnerability Analysis

The root cause is a flaw in the contract's algorithm for constructing s_positionsHash, specifically the use of the XOR operation to aggregate Keccak256 hash results. While a single hash function remains secure, the mathematical linearity of the XOR operation renders the overall fingerprint algorithm (i.e., the XOR sum of hashes) insecure [2].

Linearity implies that an attacker does not need to break the hash function itself (i.e., reversing the tokenId from the hash). Instead, they can employ a combinatorial strategy: generating a large number of random tokenIds, calculating their Keccak256(tokenId), and from these hash values, selecting a specific subset such that the XOR sum of these tokenId hashes exactly matches the victim's target fingerprint.

This allows an attacker to pass a set of forged tokenIds when calling withdraw() to pass the health check and retrieve all collateral corresponding to s_positionsHash.

Theory

Assume the user's position fingerprint s_positionsHash has a user position hash of $TT$ and numLegs of $kk$, with user tokenIds $\{t_1,t_2,\dots ,t_n\}\backslash \{t\_1,\; t\_2,\; \backslash dots,\; t\_n\backslash \}$. Thus:

$$\underset{i=1}{\overset{k}{⨁}}[\text{Hash}(t_i)(\mathrm{m}\mathrm{o}\mathrm{d}{2}^{248})]=T\backslash bigoplus\_\{i=1\}^\{k\}\; [\backslash text\{Hash\}(t\_i)\; \backslash pmod\{2^\{248\}\}]\; =\; T$$

Here, each 248-bit hash value can be viewed as a 248-dimensional vector.

$$\text{Hash}(t_i)(\mathrm{m}\mathrm{o}\mathrm{d}{2}^{248})=[b_0,b_1,\dots ,b_{247}{]}^T,where{b}_i\in \{0,1\}\backslash text\{Hash\}(t\_i)\; \backslash pmod\{2^\{248\}\}\; =\; [b\_0,\; b\_1,\; \backslash dots,\; b\_\{247\}]^T,\; where\backslash \; b\_i\; \backslash in\; \backslash \{0,\; 1\backslash \}$$

Therefore, $TT$ resides in a 248-dimensional space composed of 0s and 1s (${\mathbb{F}}_2^{248}\backslash mathbb\{F\}\_2^\{248\}$). In this space, the XOR operation is equivalent to vector addition (Appendix I).

The attacker's goal is to find $nn$ 248-dimensional vectors $\{v_1,v_2,\dots ,v_n\}\backslash \{v\_1,\; v\_2,\; \backslash dots,\; v\_n\backslash \}$ from all of the available vectors such that the lower 248 bits of their XOR sum equal $TT$. Thus, we can formulate the attacker's objective as a system of linear equations:

$$x_1{v}_1+x_2{v}_2+\cdots +x_n{v}_n=Tx\_1\; v\_1\; +\; x\_2\; v\_2\; +\; \backslash dots\; +\; x\_n\; v\_n\; =\; T$$

Specifically, we do not need to try to construct $TT$ directly. Instead, we select $nn$ linearly independent hash vectors $\{v_1,v_2,\dots ,v_n\}\backslash \{v\_1,\; v\_2,\; \backslash dots,\; v\_n\backslash \}$ (where $nn$ equals the dimension 248) and use them as column vectors to construct an $n\times nn\; \backslash times\; n$ matrix $AA$:

$$A=[v_1,v_2,\dots ,v_n]A\; =\; [v\_1,\; v\_2,\; \backslash dots,\; v\_n]$$

The problem then transforms into finding a coefficient vector $xx$ such that:

$$A\cdot x=TA\; \backslash cdot\; x\; =\; T$$

Where $x=[x_1,x_2,\dots ,x_n{]}^{T}x\; =\; [x\_1,\; x\_2,\; \backslash dots,\; x\_n]^T$, and $x_i\in \{0,1\}x\_i\; \backslash in\; \backslash \{0,\; 1\backslash \}$.

According to linear algebra theory, as long as matrix $AA$ is full rank, it spans the entire $nn$-dimensional space. This means that for any target $TT$, the system of equations has a unique solution. After solving for $xx$, we simply retain those vectors $v_{i}v\_i$ for which $x_i=1x\_i=1$; their XOR sum is $TT$.

Example

To facilitate understanding, we demonstrate this construction process with a case study. Assume the vectors are 3-dimensional, with each dimension consisting only of 0 or 1, and the target hash value is 101, i.e., $T=[1,0,1{]}^{T}T\; =\; [1,\; 0,\; 1]^T$.

Next, we randomly generate 3 hash values:

• $v_1=[1,1,0{]}^{T}v\_1\; =\; [1,\; 1,\; 0]^T$
• $v_2=[0,1,0{]}^{T}v\_2\; =\; [0,\; 1,\; 0]^T$
• $v_3=[0,1,1{]}^{T}v\_3\; =\; [0,\; 1,\; 1]^T$

We construct matrix $AA$ using these three vectors as columns and set up the equation $Ax=TAx=T$:

Solving via Gaussian elimination, we obtain $x=[1,0,1{]}^{T}x\; =\; [1,\; 0,\; 1]^T$. This means we need to select $v_{1}v\_1$ and $v_{3}v\_3$ (corresponding to $x_1=1,x_3=1x\_1=1,\; x\_3=1$), and their XOR sum exactly equals the target $TT$.

Selecting n Linearly Independent Vectors

As previously mentioned, to solve $Ax=TAx=T$, we need to construct a full-rank matrix $AA$. Given that we are dealing with an extremely large vector space ($m=2^{248}m\; =\; 2^\{248\}$), the core question is: How do we quickly select $nn$ linearly independent vectors from this vast space?

Consider the simplest method: randomly generating $nn$ tokenIds and selecting their hash results as vectors.

Over ${\mathbb{F}}_2\backslash mathbb\{F\}\_2$, the probability $PP$ that $nn$ randomly selected $nn$-dimensional vectors form a full-rank matrix is:

$$P(n)=\prod _{k=0}^{n-1}(1-\frac{2^k}{2^n})P(n)\; =\; \backslash prod\_\{k=0\}^\{n-1\}\; \backslash left(1\; -\; \backslash frac\{2^k\}\{2^n\}\backslash right)$$

When $nn$ is large (in this example, $n=248n=248$), this probability converges to a constant (Appendix II):

$$\underset{n\to \mathrm{\infty }}{\lim }P(n)\approx 0.28879\backslash lim\_\{n\; \backslash to\; \backslash infty\}\; P(n)\; \backslash approx\; 0.28879$$

This means each random attempt has approximately a 28.9% probability of success. On average, an attacker only needs about 3.5 attempts to find a set of linearly independent vectors. Therefore, the computational cost is extremely low, and the attacker can quickly construct a matrix $AA$ that satisfies the conditions.

To control the countLegs in the top 8 bits, we only need to adjust the range of the randomly generated tokenId values based on the target countLegs.

For example, if we want the numLegs in the forged fingerprint to be 0, we simply ensure that the $nn$ randomly generated tokenIds are all less than $2^{64}2^\{64\}$. Since the leg increment for tokenIds in this range is 0, regardless of which vectors the Gaussian elimination solution $xx$ selects, the final accumulated numLegs will inevitably be 0.

Attack Analysis

The white hat rescuer initiated multiple rescue transactions. For simplicity, the following discussion is based on just one of these transactions [3].

The core logic consists of the following 5 steps:

1. Borrow 0.23e8 WBTC and 28e18 WETH via flash loan from Aave.
2. Deposit 0.23e8 WBTC and 28e18 WETH into the poWBTC contract and the 0x1f8d_poWETH contract.
3. Call mintOptions() of the PanopticPool contract with a normal positionIdList to borrow funds and open a leveraged position.
4. Call withdraw(), passing the forged tokenIds. Because these forged positions have a positionSize of 0, the function returns tokenRequired as 0, meaning the total collateral required for all positions is erroneously calculated as zero. Meanwhile, the s_positionsHash generated by these tokenIds is exactly the same as the one generated in step 3, allowing the rescuer to retrieve all collateral without repaying any debt.
5. Repay the flash loan and execute the next round.

Summary

This incident highlights two compounding flaws that together enabled unauthorized collateral withdrawal.

• XOR is not a secure aggregation function for hashes. Keccak256 is collision-resistant, but XOR's linearity means the XOR sum of multiple hashes does not inherit that property. Constructing a set of inputs whose hashes XOR to any target value reduces to solving a system of linear equations over ${\mathbb{F}}_2\backslash mathbb\{F\}\_2$, which is computationally trivial. Hash composition requires operations that preserve collision resistance, such as concatenation followed by re-hashing.
• Missing validation of position IDs. The protocol did not verify whether passed positionIds corresponded to valid option positions. Values below $2^{64}2^\{64\}$ carry a countLegs of 0 and a positionSize of 0, meaning the forged positions incur no debt. This allowed the attacker to pass the health check with zero collateral requirement while matching the target fingerprint.

Reference

1. https://x.com/Panoptic_xyz/status/1961187739866644524

2. https://cseweb.ucsd.edu/~mihir/papers/inchash.pdf

3. https://app.blocksec.com/explorer/tx/eth/0x67a45dfe5ff4b190058674d7c791bbdc48e889f319f937c24fa13a5f9093f088

Appendix

The following two appendices provide a mathematical explanation and proof of the statements in the main text, namely that the XOR operation is equivalent to vector addition (Appendix I) and the probability that a random matrix is full rank (Appendix II).

Appendix I

In the finite field ${\mathbb{F}}_2=\{0,1\}\backslash mathbb\{F\}\_2\; =\; \backslash \{0,\; 1\backslash \}$, addition is defined as addition modulo 2:

Observation shows this is identical to the Exclusive OR (XOR, symbol $\oplus \backslash oplus$) logic operation.

For the $nn$-dimensional vector space ${\mathbb{F}}_2^n\backslash mathbb\{F\}\_2^n$ (in this case $n=248n=248$), the addition of two vectors $u=[u_1,\dots ,u_n{]}^{T}u\; =\; [u\_1,\; \backslash dots,\; u\_n]^T$ and $v=[v_1,\dots ,v_n{]}^{T}v\; =\; [v\_1,\; \backslash dots,\; v\_n]^T$ is defined as component-wise modulo 2 addition:

$$u+v=\left[\begin{array}{c}{u}_1+v_1(\mathrm{m}\mathrm{o}\mathrm{d}2)\\ \mathrm{⋮}\\ u_n+v_n(\mathrm{m}\mathrm{o}\mathrm{d}2)\end{array}\right]=\left[\begin{array}{c}{u}_1\oplus v_1\\ \mathrm{⋮}\\ u_n\oplus v_n\end{array}\right]=u\oplus vu\; +\; v\; =\; \backslash begin\{bmatrix\}\; u\_1\; +\; v\_1\; \backslash pmod\; 2\; \backslash \backslash \; \backslash vdots\; \backslash \backslash \; u\_n\; +\; v\_n\; \backslash pmod\; 2\; \backslash end\{bmatrix\}\; =\; \backslash begin\{bmatrix\}\; u\_1\; \backslash oplus\; v\_1\; \backslash \backslash \; \backslash vdots\; \backslash \backslash \; u\_n\; \backslash oplus\; v\_n\; \backslash end\{bmatrix\}\; =\; u\; \backslash oplus\; v$$

Therefore, in the ${\mathbb{F}}_2^n\backslash mathbb\{F\}\_2^\{n\}$ vector space, vector addition is equivalent to bitwise XOR operation on vector components.

Appendix II

To make the matrix full rank, these $nn$ vectors must be linearly independent.

The first vector $v_{1}v\_1$ can be any vector in ${\mathbb{F}}_2^n\backslash mathbb\{F\}\_2^n$ except the zero vector, providing $2^n-12^n\; -\; 1$ choices; the second vector $v_{2}v\_2$ must not reside in the subspace spanned by $\{v_1\}\backslash \{v\_1\backslash \}$, which contains $2^{1}2^1$ vectors, leaving $2^n-22^n\; -\; 2$ choices; following this logic, the $kk$-th vector $v_{k}v\_k$ cannot be in the subspace spanned by the previous $k-1k-1$ vectors, resulting in $2^n-2^{k-1}2^n\; -\; 2^\{k-1\}$ possible choices.

The total number of such matrices (i.e., the order of $GL(n,{\mathbb{F}}_2)GL(n,\; \backslash mathbb\{F\}\_2)$) is:

$$N=\prod _{k=0}^{n-1}(2^n-2^k)=(2^n-1)(2^n-2)(2^n-4)\cdots (2^n-2^{n-1})N\; =\; \backslash prod\_\{k=0\}^\{n-1\}\; (2^n\; -\; 2^k)\; =\; (2^n\; -\; 1)(2^n\; -\; 2)(2^n\; -\; 4)\backslash cdots(2^n\; -\; 2^\{n-1\})$$

And the total number of all possible $n\times nn\; \backslash times\; n$ matrices is $(2^n{)}^n=2^{n^2}(2^n)^n\; =\; 2^\{n^2\}$.

Thus, the probability $PP$ is:

$$P=\frac{\prod _{k=0}^{n-1}(2^n-2^k)}{2^{n^2}}=\prod _{k=0}^{n-1}\left(\frac{2^n-2^k}{2^n}\right)=\prod _{k=0}^{n-1}(1-\frac{2^k}{2^n})P\; =\; \backslash frac\{\backslash prod\_\{k=0\}^\{n-1\}\; (2^n\; -\; 2^k)\}\{2^\{n^2\}\}\; =\; \backslash prod\_\{k=0\}^\{n-1\}\; \backslash left(\; \backslash frac\{2^n\; -\; 2^k\}\{2^n\}\; \backslash right)\; =\; \backslash prod\_\{k=0\}^\{n-1\}\; (1\; -\; \backslash frac\{2^k\}\{2^n\})$$

Letting $j=n-kj\; =\; n\; -\; k$, we can rewrite this expression as:

$$P=\prod _{j=1}^n(1-\frac{1}{2^j})P\; =\; \backslash prod\_\{j=1\}^\{n\}\; \backslash left(1\; -\; \backslash frac\{1\}\{2^j\}\backslash right)$$

As $n\to \mathrm{\infty }n\; \backslash to\; \backslash infty$, this product converges to a constant:

$$P\approx 0.288788P\; \backslash approx\; 0.288788$$

This means that for large $nn$, the probability that a random matrix is full rank is approximately 28.9%.

About BlockSec

BlockSec is a full-stack blockchain security and crypto compliance provider. We build products and services that help customers to perform code audit (including smart contracts, blockchain and wallets), intercept attacks in real time, analyze incidents, trace illicit funds, and meet AML/CFT obligations, across the full lifecycle of protocols and platforms.

BlockSec has published multiple blockchain security papers in prestigious conferences, reported several zero-day attacks of DeFi applications, blocked multiple hacks to rescue more than 20 million dollars, and secured billions of cryptocurrencies.

• Official website: https://blocksec.com/

• Official Twitter account: https://twitter.com/BlockSecTeam

• 🔗 BlockSec Auditing Service : Submit a request

• 🔗 Phalcon Security APP: Book a demo

• 🔗 Phalcon Compliance