On November 23, 2023, there were a series of attacks targeting KyberSwap. These attacks resulted in a total loss of over $48 million. The fundamental issue originated from incorrect rounding direction during KyberSwap's reinvestment process. This subsequently led to improper tick calculations and, ultimately, to double counting of liquidity.
We've released an extensive report, "Yet Another Tragedy of Precision Loss: An In-Depth Analysis of the KyberSwap Incident", which delves into the particulars of the event. For a deeper understanding, you are encouraged to consult the full analysis. Below, we provide a succinct introduction to this incident, highlighting it as one of the top ten security incidents of 2023.
Background
KyberSwap is a decentralized automated market maker (CLAMM) platform. To meet the market demand of the concentrated liquidity, KyberSwap Elastic is launched based on Uniswap V3, with several improvements including the reinvestment curve to enable the auto-compounding of the liquidity provision yields.
1. Tick and Square Root Price
Tick in Uniswap V3-like CLAMMs is used to mark the price in a discrete manner so that the LPs can provide liquidity within a fixed range instead of the entire range (hence the term "concentrated").
Liquidity can be put in a range between any two ticks (which need not be adjacent), i.e., a pair of tick indices (a lower tick and an upper tick). Specifically, the price of each tick (at an integer index i) is defined as follows:
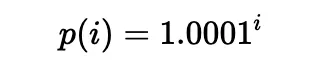
In practice, the square root price (denoted as sqrtP or sqrtPrice) is used:
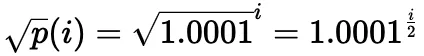
It is also possible to compute the current tick based on the current square root price:
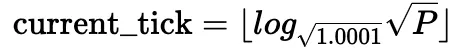
Obviously, while only a single square root price is calculated for a given tick, multiple square root prices may point to the same tick. For a more detailed explanation, please refer to the documents of Uniswap V3 and KyberSwap.
2. Reinvestment Curve
Uniswap V3-based CLAMM suffers from the pool utilization of LP fees and significant gas fees required to reinvest. Hence, KyberSwap adopted reinvestment curve to address the problem.
The key to the reinvestment curve is that the fees collected in each swap is accumulated as additional liquidity in the pool as the reinvestment liquidity within an infinite range. The reinvestment tokens are minted to the LPs and the reinvestment liquidity accumulated is allocated to the LPs accordingly. Besides, the reinvestment liquidity also participates in the swap and price calculation process.
The corresponding code for the calculations introduced above is shown in the computeSwapStep function in following code snippet of the corresponding pool.
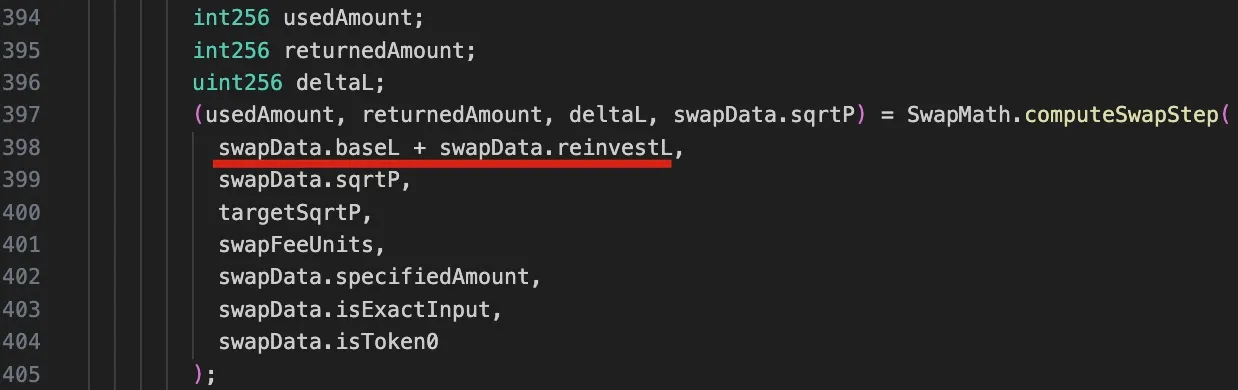
It should be noticed that due to the reinvestment liquidity, the liquidity in this function is a sum of two components: baseL for the base liquidity, and reinvestL for the accumulated liquidity for the reinvestment.
3. Swap in KyberSwap
The implementation of the swap function of the KyberSwap's pool discussed earlier can be abstracted as the below diagram:
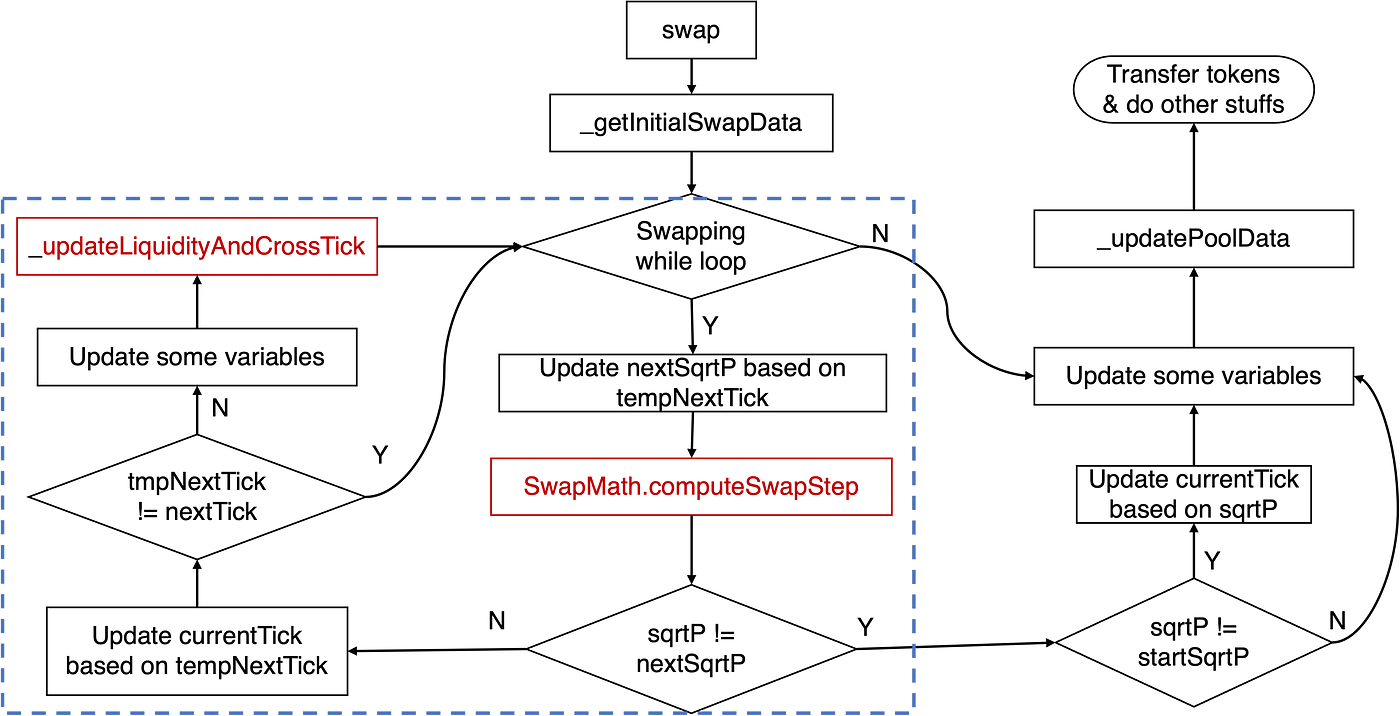
The crucial logic pertaining to the tick calculation resides within the swapping while loop, as highlighted by the blue rectangle. Specifically, the principal logic involves the computeSwapStep function and the _updateLiquidityAndCrossTick function. The former calculates key states, such as input and output amounts for the given swap and nextSqrtP, while the latter handles cases when a cross-tick occurs.
Traditionally, when the price increases, we refer to this as shifting the tick right/upward; otherwise, we say the tick moves left/downward.
To better understand the vulnerability that will be discussed later, it's essential that we explore the relevant code logic of the computeSwapStep function, as illustrated in the following figure:
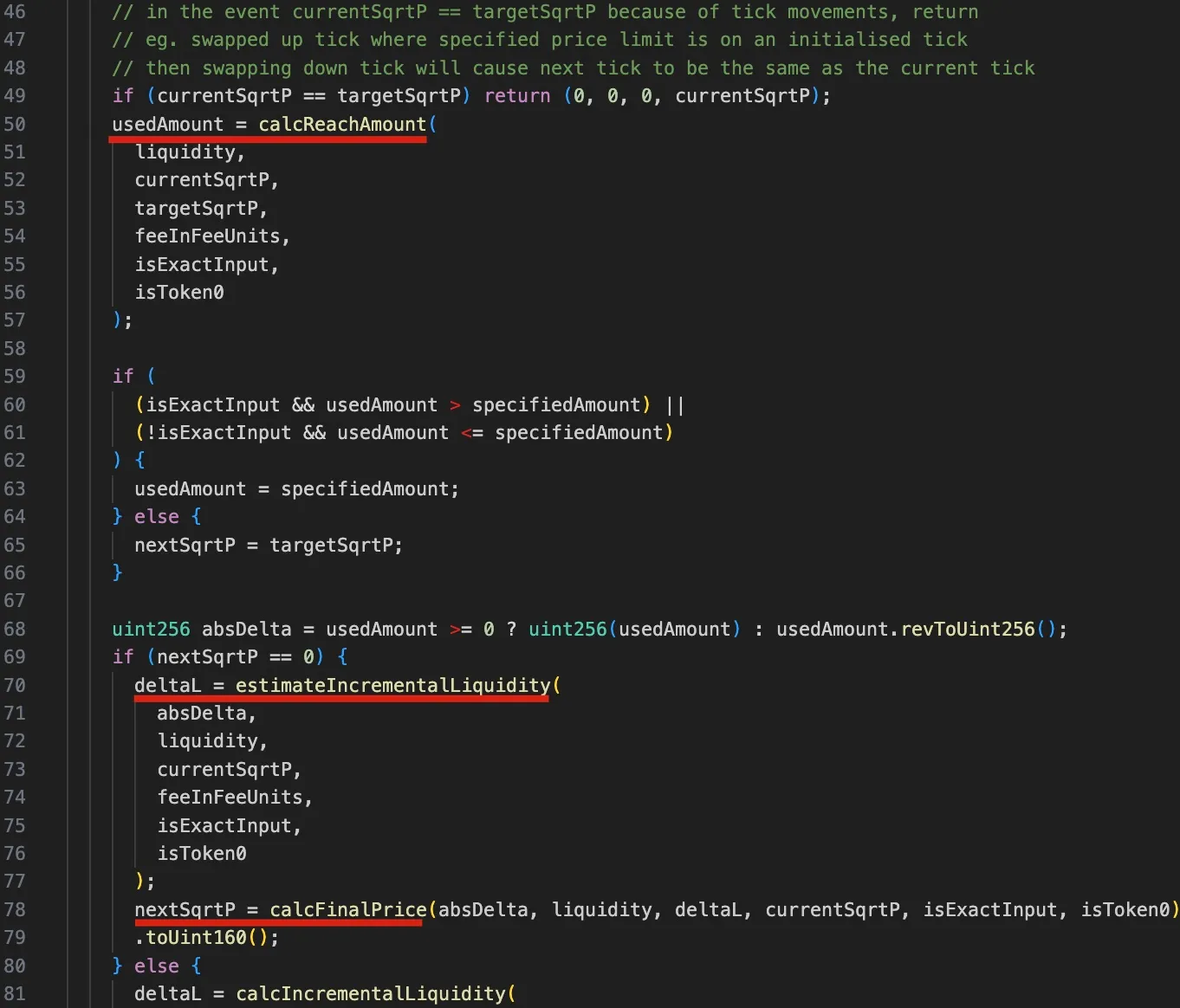
Specifically, the calcReachAmount function calculates the input tokens needed for the target price targetSqrtP (lines 50-57). If the usedAmount is greater than specifiedAmount, the tick isn't crossed, and nextSqrtP is calculated from deltaL (i.e., the delta liquidity, lines 59-62). deltaL is determined using the estimateIncrementalLiquidity function, and the final price nextSqrtP is calculated with the calcFinalPrice function (lines 70-79). If less input is needed, nextSqrtP is set to the next tick's price, but this case isn't used in the attack.
The steps outlined above make clear that if the tick is not crossed, the nextSqrtP returned by computeSwapStep should not be larger than the sqrtP of the next tick. However, due to the dependency of the price on the liquidty (base liquidity and delta liquidity) and precision loss, the attackers is able to manipulate the nextSqrtP to be larger while the tick is not crossed.
Vulnerability Analysis
The root cause lies in the flawed tick calculation caused by the incorrect rounding direction within the delta liquidity calculation (i.e., the estimateIncrementalLiquidity function) of the SwapMath contract (which is invoked by the computeSwapStep function). This, in turn, improperly affects the tick calculation later.
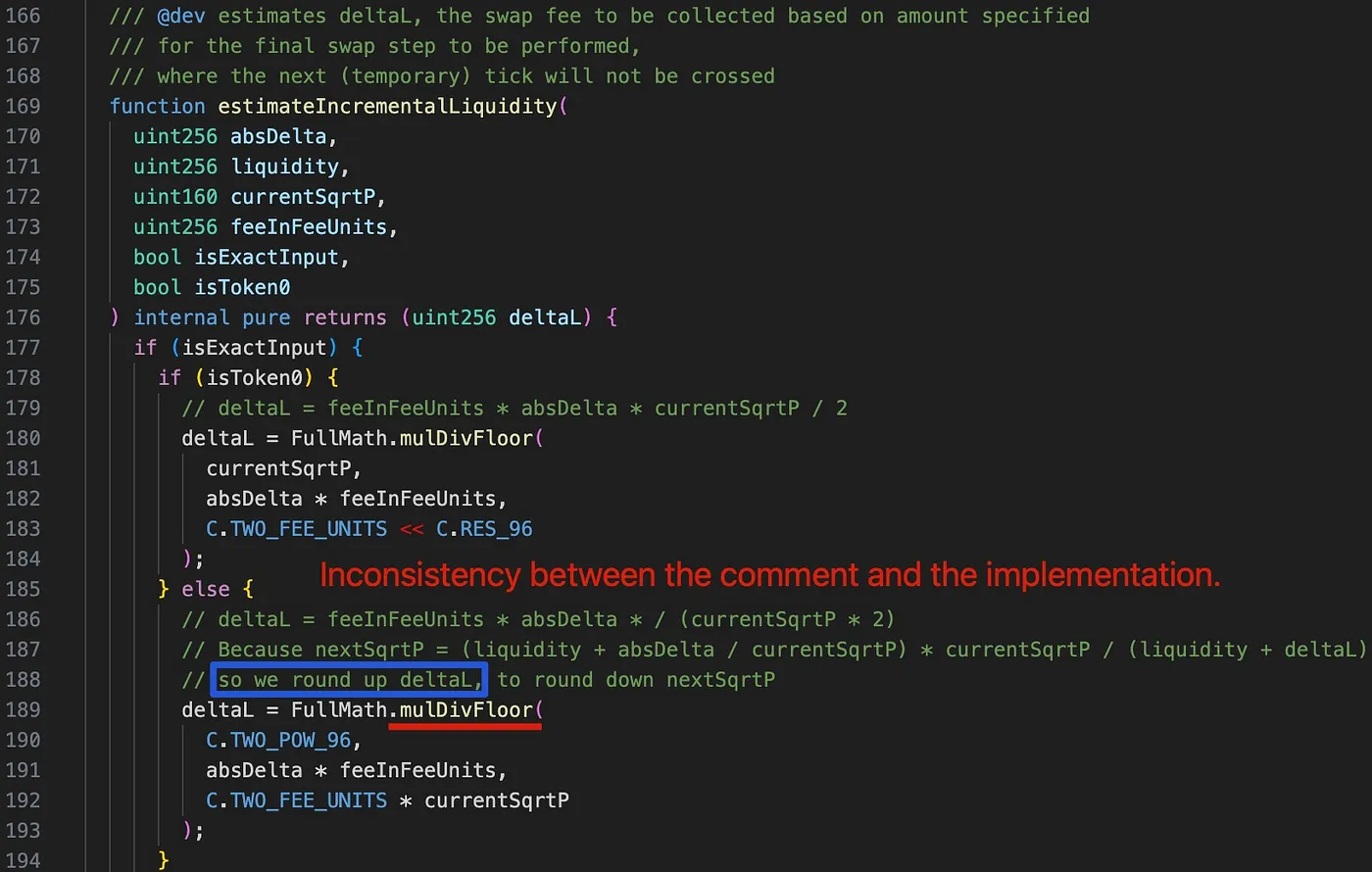
Interestingly, upon examining the comment at line 188 (highlighted by the blue rectangle), we find that deltaL is intended to be rounded up in order to round down the nextSqrtP. However, deltaL is mistakenly rounded down due to the use of the mulDivFloor function at line 189. Consequently, nextSqrtP is inaccurately rounded up.
Attack Analysis
The attackers initiated multiple attack transactions, with each transaction draining multiple pools. For the sake of simplicity, the following discussion is based on the first attack within the attack transaction.
The core attack logic consists of the following six steps:
-
Borrowing 2,000 WETH via flash loan from AAVE.
-
Swapping 6.850 WETH for 6.371 frxETH in the victim pool 0xfd7b. This step is used to push current tick and
currentSqrtPinto a location where currently no liquidity is present.
currentSqrtPseems to be randomly chosen by the attacker, and the swap stops at this price precisely.- Base liquidity (
baseL) is zero after this step, but the reinvestment liquidity (reinvestL) is non-zero.
- Adding liquidity into the pool and then removing part of the liquidity. This step is used to control the range and total liquidity to a desired amount.
- The tick range is chosen based on the
currentSqrtP. - The desired liquidity for the attack could be derived from the tick range, although the corresponding calculation logic requires further exploration.
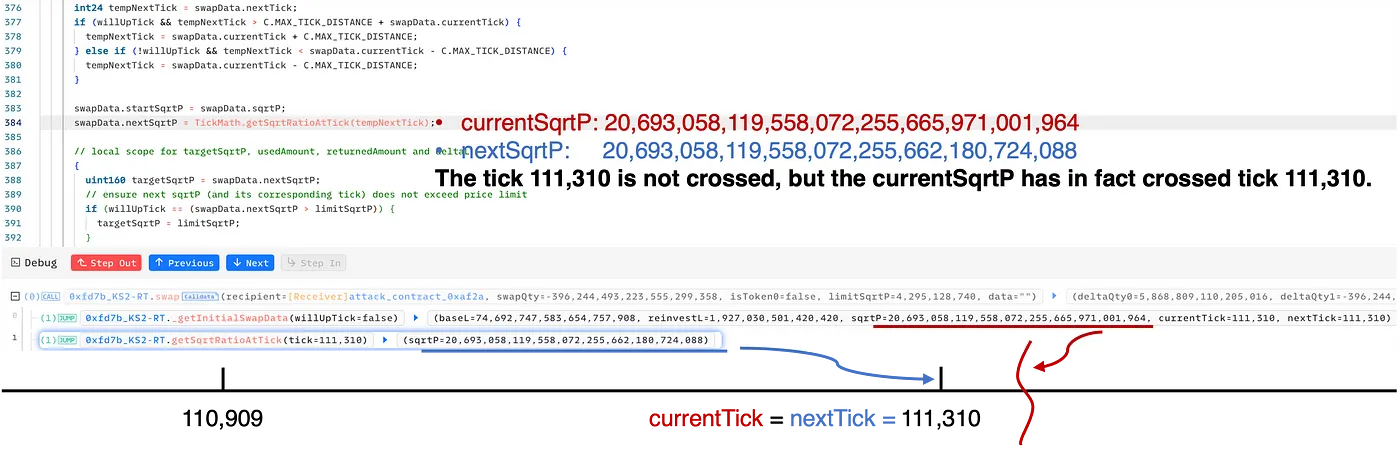
- Swapping 387.170 WETH for 0.06 frxETH in the pool. This step is used to manipulate the current tick so that
nextTick==currentTick. Specifically, the swap in step 4 cunningly deceives the pool into believing that the tick 111,310 is not crossed. However, in reality, thecurrentSqrtPis indeed greater than thesqrtPof tick 111,310.
- Swapping 0.06 frxETH for 396.244 WETH in the pool. Note that the swapping direction is opposite compared to the previous step. In this step, liquidity is double counted to make the swap profitable and consequently drain the pool.
- Repaying the flash loan, and harvesting 6.364WETH and 1.117 frxETH.
For an in-depth examination, please refer to our comprehensive analysis, which includes more details with calculations and figures.
Summary
The fundamental issue in this incident stems from incorrect rounding during KyberSwap's reinvestment process, leading to inaccurate tick calculations and ultimately to double liquidity counting. This incident highlights the intricate and elusive nature of precision loss problems within DeFi protocols, posing a serious challenge to the entire community.
This 2023 attack stands out for its complexity, featuring exceptionally nuanced calculations and serving as a prime example of the many precision-related security incidents that have significantly tested the community. Moreover, after extensive negotiations with authorities, the attacker issued a provocatively toned message to the public, asserting a demand for total control over the protocol.
Read other articles in this series:
- Lead-In: Top Ten "Awesome" Security Incidents in 2023
- #1: Harvesting MEV Bots by Exploiting Vulnerabilities in Flashbots Relay
- #2: Euler Finance Incident: The Largest Hack of 2023
- #4: Curve Incident: Compiler Error Produces Faulty Bytecode from Innocent Source Code
- #5: Platypus Finance: Surviving Three Attacks with a Stroke of Luck
- #6: Hundred Finance Incident: Catalyzing the Wave of Precision-Related Exploits in Vulnerable Forked Protocols
- #7: ParaSpace Incident: A Race Against Time to Thwart the Industry's Most Critical Attack Yet
- #8: SushiSwap Incident: A Clumsy Rescue Attempt Leads to a Series of Copycat Attacks
- #9: MEV Bot 0xd61492: From Predator to Prey in an Ingenious Exploit
- #10: ThirdWeb Incident: Incompatibility Between Trusted Modules Exposes Vulnerability