Yet Another Tragedy of Precision Loss: An In-Depth Analysis of the KyberSwap Incident

2023年11月23日，我们观察到一系列针对KyberSwap的攻击。这些攻击导致总损失超过4800万美元。我们初步分析表明，此次漏洞利用源于tick操纵和流动性双重计算。然而，由于篇幅限制，我们无法在文中深入探讨。尽管随后其他安全研究人员进行了有见地的分析，但该问题的根本原因——精度损失——仍未暴露。

有趣的是，几天后事态变得更加复杂。2023年11月30日，经过与官方多轮讨论，攻击者发送了一条消息，在外界看来充满挑衅，要求完全控制。抛开这一点不谈，攻击者还透露了一个关键信息：问题确实与精度损失有关，如下图所示。这一揭示进一步证实了我们的调查证据。因此，我们的目标是在本报告中提供一个全面的分析。

主要发现（TL;DR）

我们的调查显示，根本问题源于KyberSwap再投资过程中错误的舍入方向。这随后导致了不正确的tick计算，并最终导致流动性双重计算。
此事件凸显了DeFi协议中精度损失问题的复杂性和隐蔽性，给整个社区带来了严峻的挑战。
这些攻击的频繁发生，严峻地提醒我们主动威胁预防措施的极端重要性，这可以极大地帮助减少未来的损失。

在接下来的章节中，我们将首先介绍KyberSwap的一些关键背景信息。随后，我们将对该漏洞及相关攻击进行深入分析。

0x1 背景

KyberSwap[1]是一个去中心化的自动做市商（CLAMM）平台。为了满足集中流动性市场需求，KyberSwap Elastic[3]在Uniswap V3[2]的基础上推出，并进行了一些改进，包括再投资曲线，以实现流动性提供收益的自动复利。

0x1.1 Tick和平方根价格

Uniswap V3类CLAMM中的Tick用于离散地标记价格，以便LP可以在固定范围内而非整个范围（因此称为“集中式”）提供流动性[4]。

为了让LP能够指定具有自定义价格区间的流动性头寸，协议需要一种方法来跟踪跨越各种价格点的聚合流动性。Uniswap V3通过将可能的价格空间划分为离散的“ticks”，LP可以贡献介于任意两个ticks之间的流动性来实现这一点。

根据[5]，流动性可以放置在任意两个tick之间（不必相邻），即一对tick索引（一个较低tick和一个较高tick）。具体来说，每个tick的价格（在整数索引i处）定义如下：

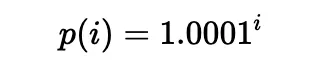
实际上，使用的是平方根价格（表示为sqrtP或sqrtPrice）：

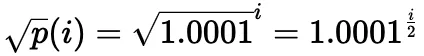
也可以根据当前平方根价格计算当前tick：

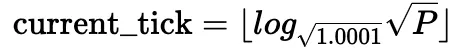
将平方根价格与流动性L结合使用是一种避免同时变化的实用方法。具体来说，当在tick内进行兑换时，价格会发生变化；当跨越tick，或增发或销毁流动性时，流动性会发生变化。有关更详细的解释，请参阅Uniswap V3的白皮书[5]。

显然，虽然对于给定的tick只计算一个平方根价格，但多个平方根价格可能指向同一个tick。

0x1.2 再投资曲线

基于Uniswap V3的CLAMM存在LP费用池利用率低以及再投资所需Gas费用高昂的问题。因此，KyberSwap采用了再投资曲线[6]来解决这个问题：

再投资曲线的设计目的是为了在集中流动性模型中对否则未使用的LP费用进行本地再投资。这意味着集中流动性头寸的LP费用可以自动复利，无需Gas费用或手动管理开销。此外，LP仍然可以选择在任何时候单独收取其自动复利 Fee 收益。

再投资曲线的关键在于，每次兑换收取的费用作为额外流动性累积到池中，成为无限范围内的“再投资流动性”。为LP铸造再投资代币，并将累积的再投资流动性相应地分配给LP。此外，再投资流动性也参与兑换和价格计算过程。

准确地说，而不是恒定乘积公式：

费用在每次兑换中累积到ΔL：

在（假设价格偏差低于阈值的）情况下，ΔL的计算可以简化为：

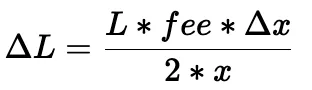
然后，从修改后的恒定乘积公式可以得出兑换金额和最终价格：

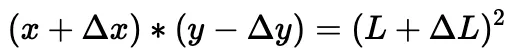
上述计算的相应代码显示在以下代码片段的computeSwapStep函数中，该片段来自相应的池。

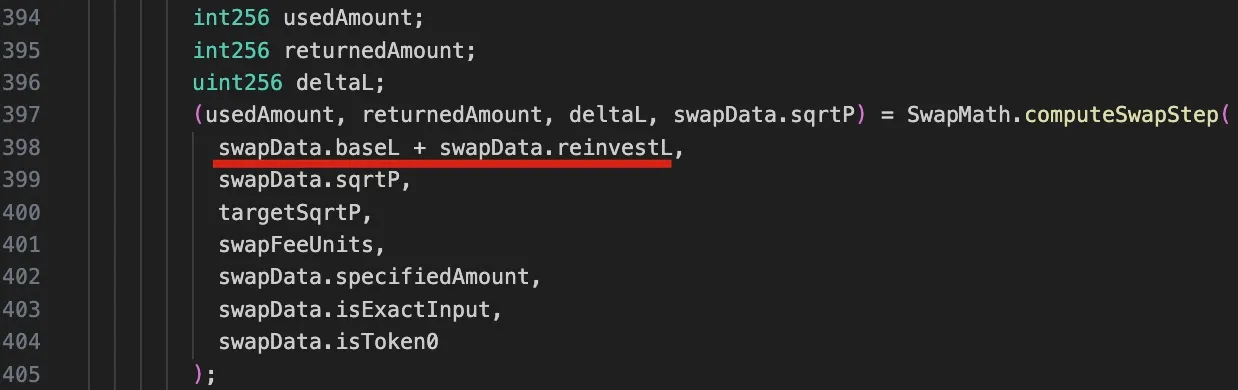
需要注意的是，由于再投资流动性，此函数中的liquidity是两个组成部分的总和：baseL代表基础流动性，reinvestL代表累积的再投资流动性。

0x1.3 KyberSwap中的兑换

Uniswap V3的兑换控制流程可以按如下方式描述[5]：

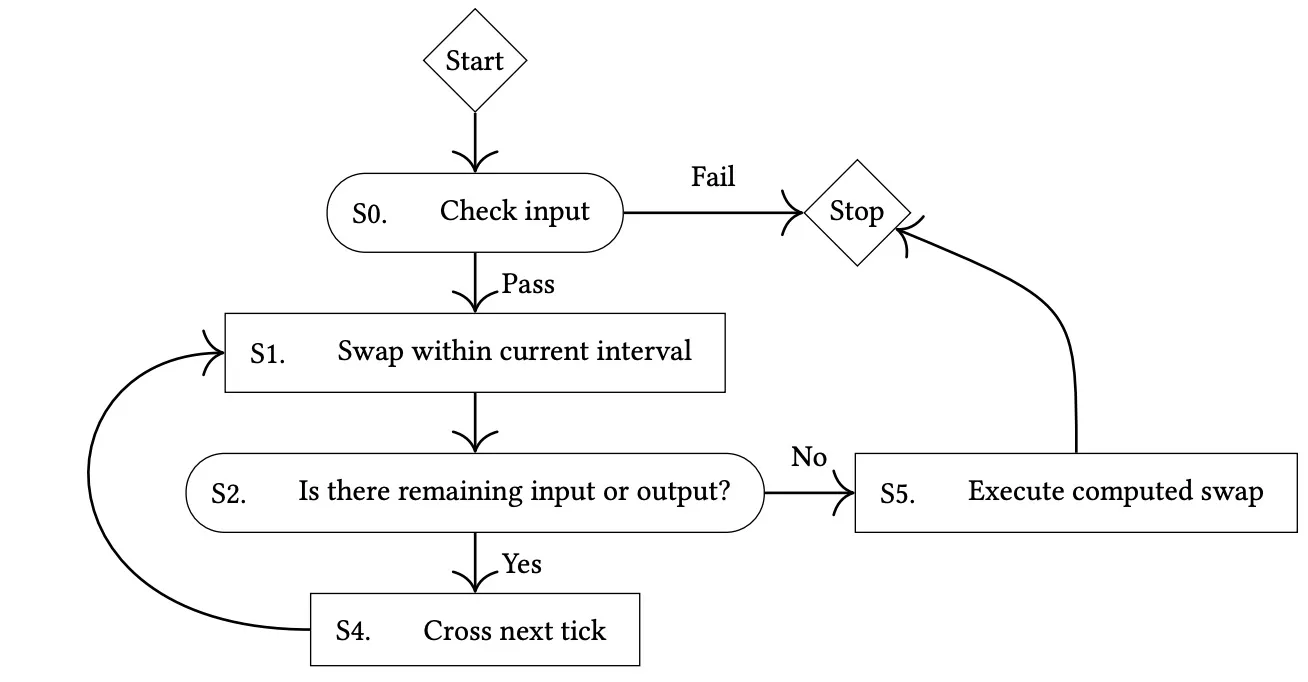
相应地，上述KyberSwap池的swap函数的实现可以抽象为下图：

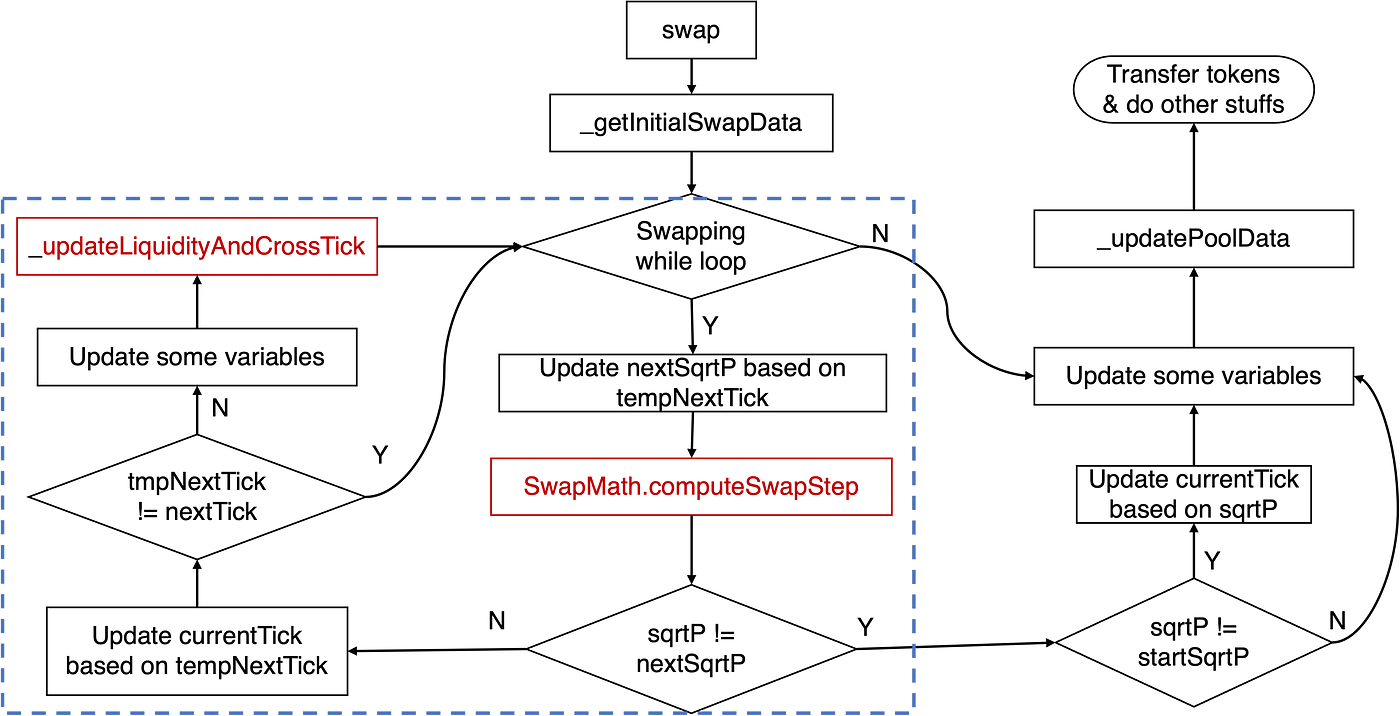
与tick计算相关的关键逻辑存在于兑换while循环中，由蓝色矩形突出显示。具体来说，主要逻辑涉及computeSwapStep函数和_updateLiquidityAndCrossTick函数。前者计算给定兑换的输入输出金额和nextSqrtP等关键状态，后者处理跨tick的情况。

传统上，当价格上涨时，我们将其称为tick向右/向上移动；否则，我们说tick向左/向下移动。

为了更好地理解稍后将讨论的漏洞，我们必须探讨computeSwapStep函数的相关代码逻辑，如下图所示：

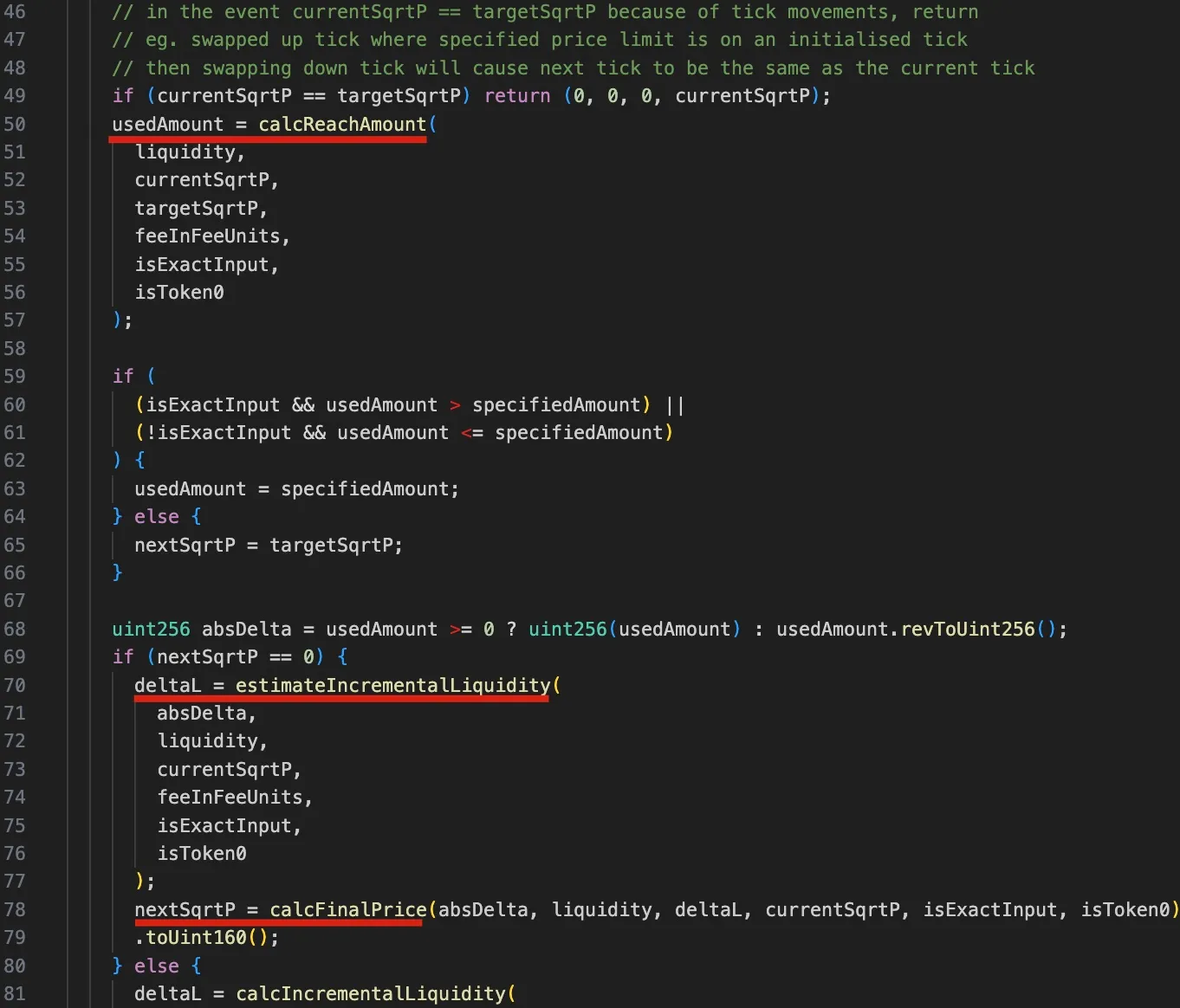
首先，从第50到57行，调用calcReachAmount函数计算达到targetSqrtP（下一个tick或用户指定的目標價格）所需的输入代币数量。

接下来，在第59至62行，进行测试以确定是否应跨越tick。

具体来说，如果使用的金额（usedAmount）大于精确输入兑换中用户指定的金额（specifiedAmount）（攻击中使用的场景），则意味着不应跨越tick，并且需要从增量流动性（deltaL，即delta流动性）导出nextSqrtP。

随后，在第70至79行，deltaL（deltaL）通过输入金额、当前流动性和价格使用estimateIncrementalLiquidity函数导出。最后，在calcFinalPrice函数中使用deltaL、输入金额、当前价格和流动性计算兑换后的最终价格nextSqrtP。

相反，如果所需金额小于用户指定的金额（这意味着nextSqrtP > 0），则使用当前和目标sqrtP计算deltaL，并且nextSqrtP是下一个tick的sqrtP。由于此分支在攻击中未使用，因此省略了详细信息。

上述步骤清楚地表明，如果未跨越tick，computeSwapStep函数返回的nextSqrtP不应大于下一个tick的sqrtP。然而，由于价格依赖于流动性（基础流动性和增量流动性）和精度损失，攻击者能够操纵nextSqrtP使其在未跨越tick时更大。

0x2 漏洞分析

根本原因在于SwapMath合约（由computeSwapStep函数调用）的增量流动性计算（即estimateIncrementalLiquidity函数）中错误的舍入方向导致了错误的tick计算。这反过来又会不当影响后续的tick计算。

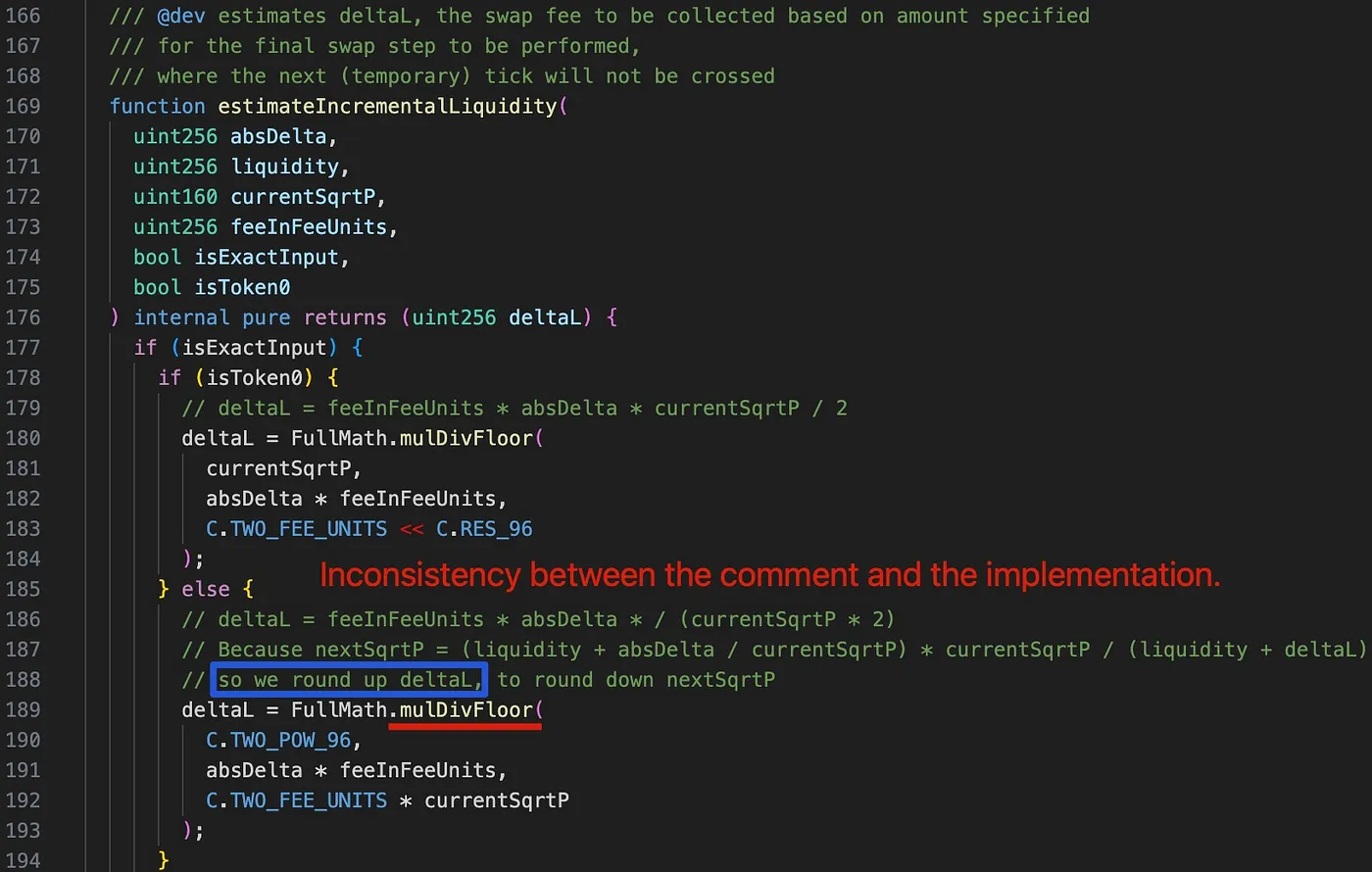
有趣的是，在检查第188行（由蓝色矩形突出显示）的注释时，我们发现deltaL本应向上舍入，以便向下舍入nextSqrtP。然而，由于在第189行使用了mulDivFloor函数，deltaL被错误地向下舍入了。因此，nextSqrtP被错误地向上舍入了。

0x3 攻击分析

攻击者发起的多笔攻击交易，每笔交易都耗尽了多个池。为简化起见，以下讨论基于攻击交易中的首次攻击。

核心攻击逻辑包括以下六个步骤：

通过AAVE的闪贷借入2000 WETH。
在受害池0xfd7b中，用6.850 WETH兑换6.371 frxETH。此步骤用于将当前tick和currentSqrtP推到一个当前没有流动性的位置。

currentSqrtP似乎由攻击者随机选择，并且兑换在此价格点精确停止。
此步骤后基础流动性（baseL）为零，但再投资流动性（reinvestL）非零。

向池中添加流动性，然后移除部分流动性。此步骤用于将范围和总流动性控制到所需金额。

Tick范围根据currentSqrtP选择。
所需的攻击流动性可以从Tick范围导出，尽管相应的计算逻辑需要进一步研究。

在池中用387.170 WETH兑换0.06 frxETH。此步骤用于操纵当前tick，使**nextTick == currentTick**。

输入金额根据流动性和currentSqrtP选择。

在池中用0.06 frxETH兑换396.244 WETH。请注意，兑换方向与上一步相反。在此步骤中，流动性被双重计算，以使兑换有利可图，从而耗尽池。
偿还闪贷，并收获6.364 WETH和1.117 frxETH。

显然，最后两次兑换（步骤4和步骤5）是操纵tick计算并使兑换有利可图以耗尽池子的关键攻击步骤。我们将在以下子节中深入探讨细节。

重要的是要注意，第3步对于操纵流动性至关重要。由于需要通过舍入操作进行精确的tick操纵，直接添加流动性来实现目标是不可行的。流动性移除是为了精确控制攻击者所需的范围内的流动性。

0x3.1 步骤4：操纵当前tick和`currentSqrtP`

在之前的步骤（步骤1和2）之后，攻击者已经准备好了用于操纵的Tick范围和流动性。具体来说：

currentSqrtP处于所需位置
当前tick = 110,909，下一个tick = 111,310，环绕着currentSqrtP

此步骤进行WETH与frxETH的兑换。在computeSwapStep函数中，我们有以下执行跟踪：

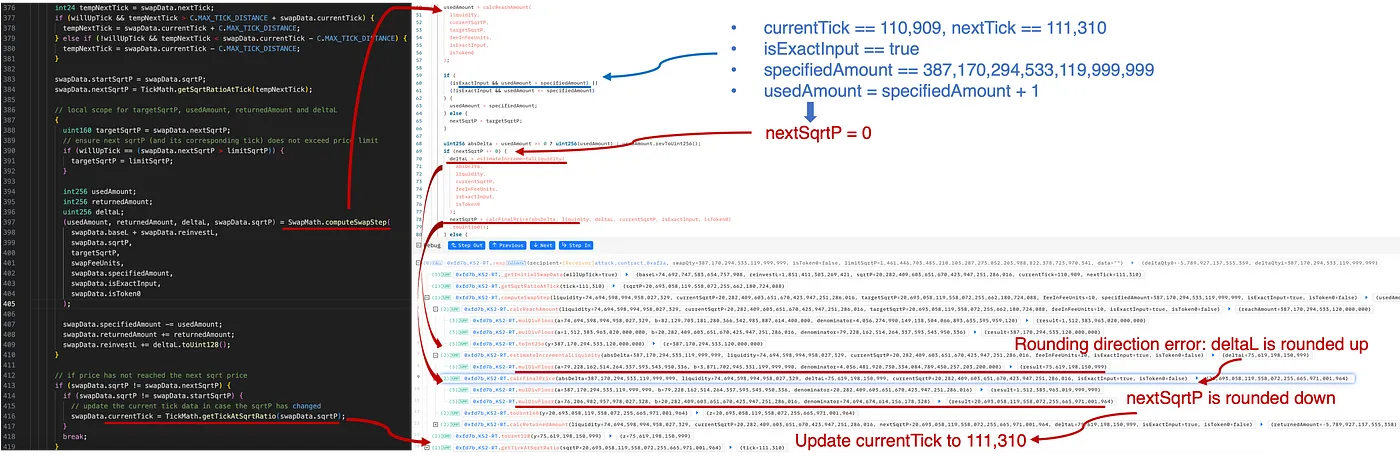
如上图所示，达到目标（即下一个tick）所需的金额将通过调用calcReachAmount函数来计算：

usedAmount = calcReachAmount(liquidity, currentSqrtP, targetSqrtP)

请注意，此计算可以在兑换之前完成。通过仔细选择specifiedAmount（usedAmount = specifiedAmount + 1），攻击者控制了兑换，使得目标（即下一个tick 111,310）未被达到，导致nextSqrtP = 0。

在这种情况下，由于tick未被跨越，nextSqrtP（即最终价格）需要从增量流动性（作为兑换费用累积）导出。

首先，通过以下方式计算来自费用的增量流动性deltaL：

deltaL = estimateIncrementalLiquidity(absDelta, currentSqrtP)

然后是最终价格nextSqrtP：

nextSqrtP = calcFinalPrice(absDelta, liquidity, deltaL, currentSqrtP)

回顾上一节讨论的舍入方向错误，此处deltaL被错误地向下舍入，导致nextSqrtP被向上舍入。具体来说，在此情况下，基于相同的absDelta（387,170,294,533,119,999,999），由于舍入方向的变化，计算结果有所不同：

因此，在步骤4的tick操纵之后，当前状态总结如下：

currentSqrtP为20,693,058,119,558,072,255,665,971,001,964，略大于Tick 111,310的sqrtP（Tick 111,310的sqrtP = 20,693,058,119,558,072,255,662,180,724,088）。
当前tick = 111,310，下一个tick = 111,310

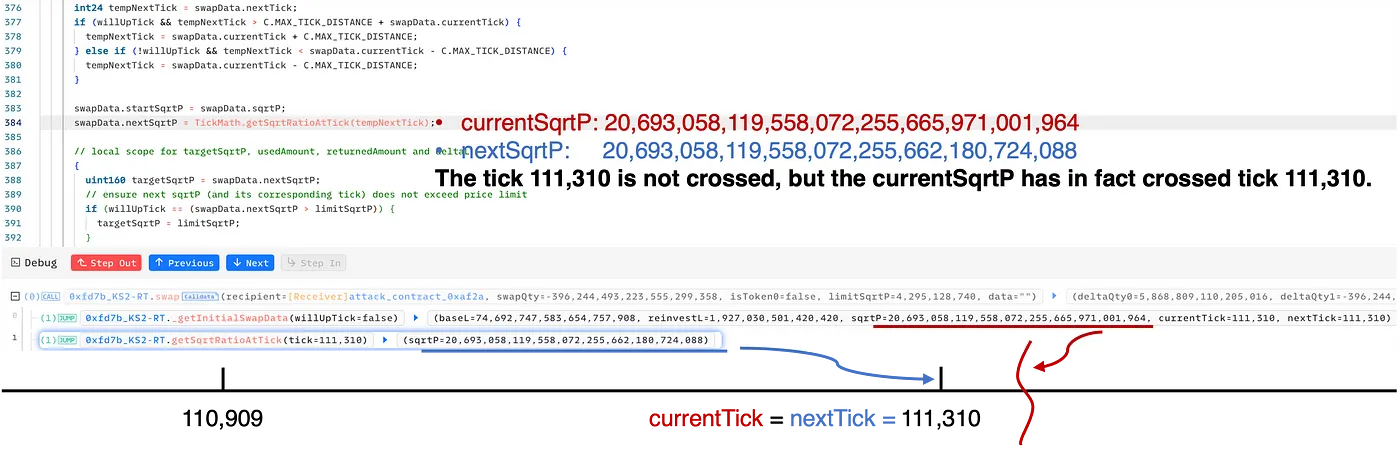
如上图所示，步骤4中的兑换巧妙地欺骗了池子，让它相信Tick 111,310并未被跨越。然而，实际上，currentSqrtP确实大于Tick 111,310的sqrtP。

0x3.2 步骤5：流动性双重计算

基于步骤4的操纵，步骤5中的攻击逻辑相对简单。此时，攻击者策划了一次从frxETH到WETH的反向兑换，这将使Tick和currentSqrtP向左移动。具体来说，computeSwapStep函数在循环中被调用了两次，这最终以一种不可预见的方式触发了流动性双重计算[7]，从而产生了额外的利润。

如上所示：

在computeSwapStep函数的第一次调用中，currentSqrtP被移至Tick 111,310的sqrtP。这是一个微小的兑换，仅使用了3 wei的frxETH来实际达到Tick 111,310。随后，在_updateLiquidityAndCrossTick函数中，当前Tick应该跨越Tick 111,310（向左/向下移动），尽管它在步骤4中并未真正向右/向上跨越Tick 111,310。这导致Tick 111,310处的流动性被计算了两次。
在computeSwapStep函数的第二次调用中，先前流动性的双重计算可能导致额外的利润。具体来说，通过利用这种流动性双重计算，最后一步的兑换价格被扭曲，导致兑换出更多的WETH，从而产生利润。