Yet Another Tragedy of Precision Loss: An In-Depth Analysis of the KyberSwap Incident

Am 23. November 2023 beobachteten wir eine Reihe von Angriffen auf KyberSwap. Diese Angriffe führten zu einem Gesamtverlust von über 48 Mio. $. Unsere erste Analyse deutete darauf hin, dass der Exploit auf Tick-Manipulation und doppelte Liquiditätszählung zurückzuführen war. Aufgrund von Platzbeschränkungen können wir jedoch nicht auf die ausführlichen Details in diesem Beitrag eingehen. Trotz anschließender aufschlussreicher Analysen anderer Sicherheitsexperten blieb die Grundursache des Problems – der Präzisionsverlust – unaufgedeckt.

Interessanterweise wurde die Lage mehrere Tage später komplizierter. Am 30. November 2023, nach mehreren Diskussionsrunden mit Beamten, sendete der Angreifer eine Nachricht, die nach außen hin voller Provokation erschien und die vollständige Kontrolle forderte. Davon abgesehen enthüllte der Angreifer auch eine entscheidende Information: Das Problem hängt tatsächlich mit Präzisionsverlust zusammen, wie die folgende Abbildung zeigt. Diese Enthüllung verstärkt die Beweise für unsere Untersuchung. Daher ist es unser Ziel, in diesem Bericht eine umfassende Analyse vorzulegen.

Wichtigste Erkenntnisse (TL;DR)

Unsere Untersuchung zeigt, dass das grundlegende Problem aus der falschen Rundungsrichtung während des Reinvestitionsprozesses von KyberSwap stammt. Dies führt anschließend zu einer fehlerhaften Tick-Berechnung und schließlich zur doppelten Liquiditätszählung.
Dieser Vorfall unterstreicht die komplexe und heimtückische Natur von Präzisionsverlustproblemen in DeFi-Protokollen, was eine erhebliche Herausforderung für die gesamte Community darstellt.
Die Häufigkeit dieser Angriffe dient als deutliche Erinnerung an die kritische Notwendigkeit proaktiver Maßnahmen zur Gefahrenabwehr, die maßgeblich zur Reduzierung zukünftiger Verluste beitragen könnten.

In den folgenden Abschnitten werden wir zunächst einige wichtige Hintergrundinformationen zu KyberSwap liefern. Anschließend werden wir eine eingehende Analyse der Schwachstelle und des damit verbundenen Angriffs durchführen.

0x1 Hintergrund

KyberSwap[1] ist eine dezentrale Automated Market Maker (CLAMM)-Plattform. Um der Marktnachfrage nach konzentrierter Liquidität gerecht zu werden, wurde KyberSwap Elastic[3] auf Basis von Uniswap V3[2] eingeführt, mit mehreren Verbesserungen, darunter die Reinvestitionskurve, die eine automatische Aufstockung der Erträge aus der Liquiditätsbereitstellung ermöglicht.

0x1.1 Tick und Quadratwurzelpreis

Der Tick in Uniswap V3-ähnlichen CLAMMs wird verwendet, um den Preis diskret zu kennzeichnen, sodass LPs Liquidität innerhalb eines bestimmten Bereichs anstelle des gesamten Bereichs bereitstellen können (daher der Begriff "konzentriert")[4].

Um LPs die Angabe von Liquiditätspositionen mit benutzerdefinierten Preisintervallen zu ermöglichen, benötigte das Protokoll eine Möglichkeit, die aggregierte Liquidität über verschiedene Preispunkte hinweg zu verfolgen. Uniswap V3 erreichte dies, indem der Raum möglicher Preise in diskrete "Ticks" unterteilt wurde, wodurch LPs Liquidität zwischen beliebigen zwei Ticks bereitstellen konnten.

Laut [5] kann Liquidität in einem Bereich zwischen zwei beliebigen Ticks (die nicht nebeneinander liegen müssen), d.h. einem Paar von Tick-Indizes (ein unterer Tick und ein oberer Tick), platziert werden. Insbesondere ist der Preis jedes Ticks (bei einem ganzzahligen Index i) wie folgt definiert:

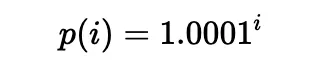
In der Praxis wird die Quadratwurzel des Preises (bezeichnet als sqrtP oder sqrtPrice) verwendet:

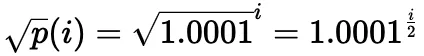
Es ist auch möglich, den aktuellen Tick anhand des aktuellen Quadratwurzelpreises zu berechnen:

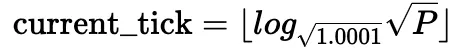
Die Verwendung des Quadratwurzelpreises zusammen mit der Liquidität L ist eine praktische Methode, um gleichzeitige Änderungen zu vermeiden. Insbesondere ändert sich der Preis beim Tauschen innerhalb eines Ticks; die Liquidität ändert sich beim Überqueren eines Ticks oder beim Erzeugen oder Verbrauchen von Liquidität. Eine detailliertere Erklärung finden Sie im Whitepaper von Uniswap V3[5].

Offensichtlich gilt: Während für einen gegebenen Tick nur ein einziger Quadratwurzelpreis berechnet wird, können mehrere Quadratwurzelpreise auf denselben Tick verweisen.

0x1.2 Reinvestitionskurve

CLAMMs, die auf Uniswap V3 basieren, leiden unter der Auslastung von LP-Gebühren und den erheblichen Gasgebühren, die für die Reinvestition erforderlich sind. Daher hat KyberSwap eine Reinvestitionskurve[6] übernommen, um das Problem zu lösen:

Die Reinvestitionskurve wurde mit dem alleinigen Zweck entwickelt, nicht genutzte LP-Gebühren im konzentrierten Liquiditätsmodell nativ zu reinvestieren. Das bedeutete, dass LP-Gebühren für konzentrierte Liquiditätspositionen automatisch ohne Gasgebühren oder manuellen Verwaltungsaufwand kompoundiert wurden. Darüber hinaus hatten LPs weiterhin die Möglichkeit, ihre automatisch kompoundierten Gebührenerlöse jederzeit separat abzuheben.

Der Kern der Reinvestitionskurve besteht darin, dass die bei jedem Swap erhobenen Gebühren als zusätzliche Liquidität im Pool als Reinvestitionsliquidität über einen unendlichen Bereich angesammelt werden. Die Reinvestitionstoken werden an die LPs ausgegeben und die angesammelte Reinvestitionsliquidität wird entsprechend den LPs zugeteilt. Außerdem nimmt die Reinvestitionsliquidität am Swap- und Preisberechnungsprozess teil.

Genauer gesagt, anstelle der Formel des konstanten Produkts:

werden die Gebühren in jedem Swap in ΔL akkumuliert:

Die Berechnung von ΔL kann vereinfacht werden (unter der Annahme, dass die Preisabweichung geringer als ein Schwellenwert ist):

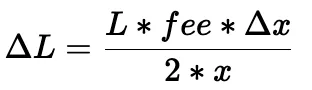
Dann können der Swap-Betrag und der Endpreis aus der modifizierten Formel des konstanten Produkts abgeleitet werden:

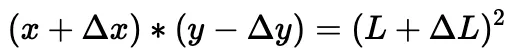
Der entsprechende Code für die oben genannten Berechnungen ist in der Funktion computeSwapStep im folgenden Code-Snippet des entsprechenden Pools zu sehen.

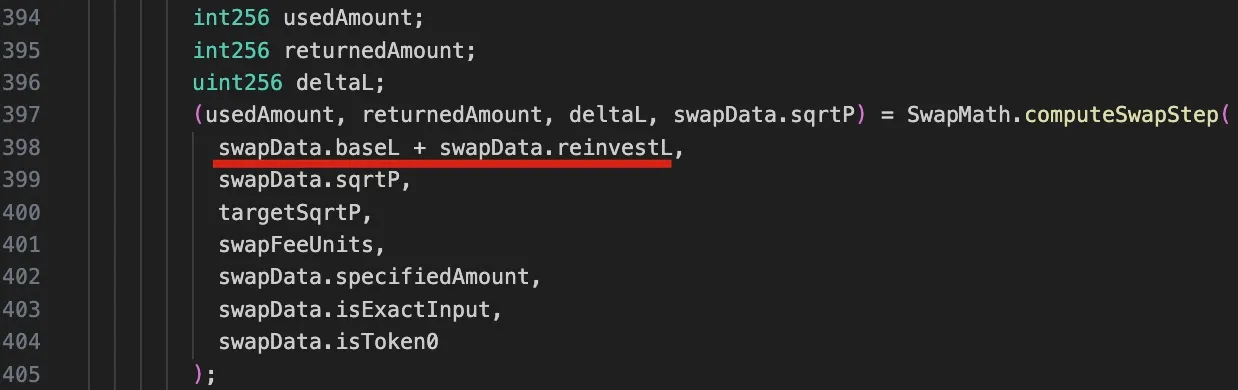
Es ist zu beachten, dass aufgrund der Reinvestitionsliquidität die liquidity in dieser Funktion eine Summe aus zwei Komponenten ist: baseL für die Basisliquidität und reinvestL für die angesammelte Liquidität für die Reinvestition.

0x1.3 Swap in KyberSwap

Der Kontrollfluss eines Swaps in Uniswap V3 kann wie folgt dargestellt werden[5]:

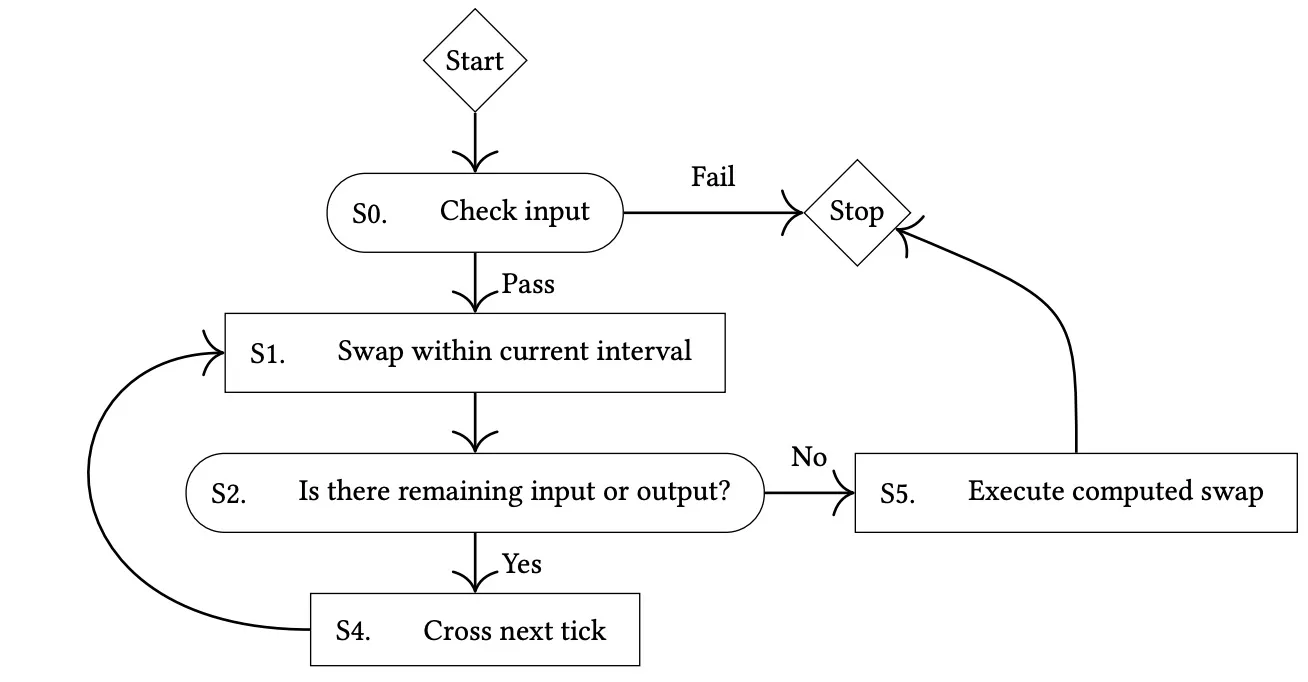
Dementsprechend kann die Implementierung der swap-Funktion des besprochenen KyberSwap-Pools als das folgende Diagramm abstrahiert werden:

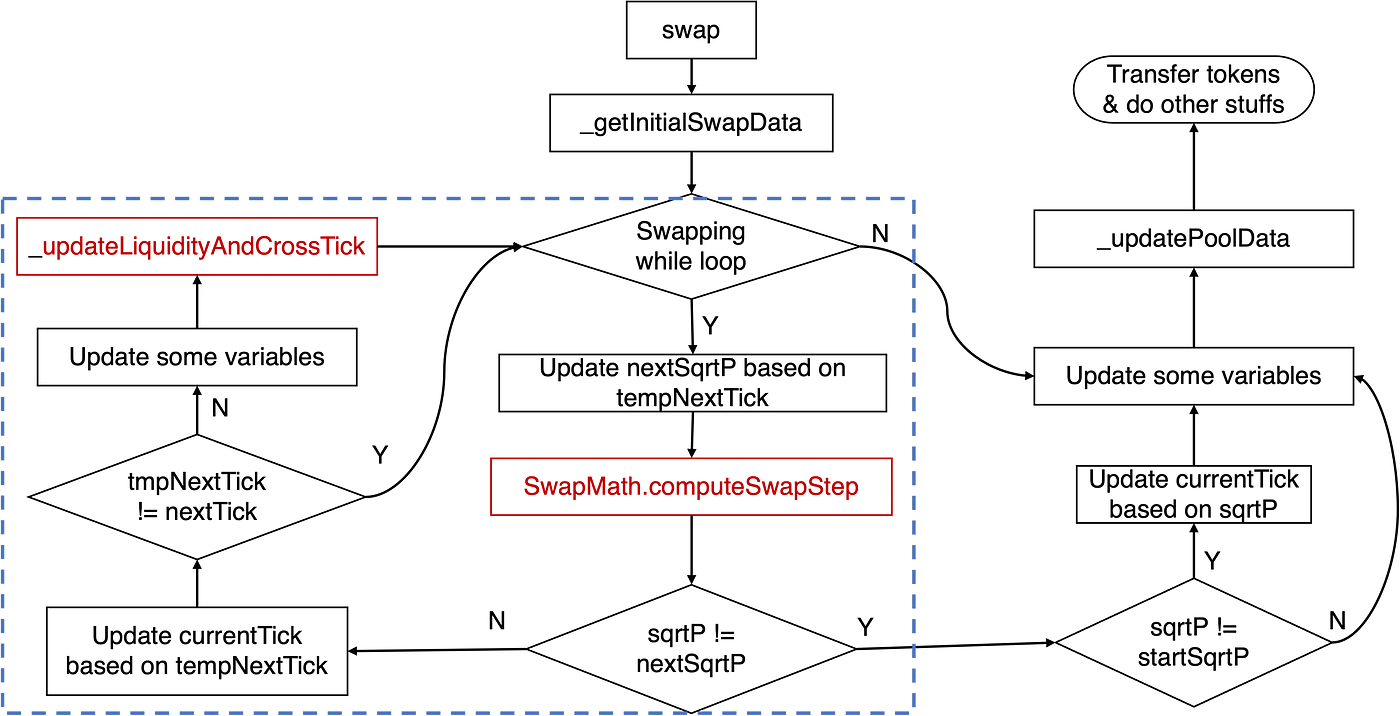
Die entscheidende Logik bezüglich der Tick-Berechnung liegt in der Swap-While-Schleife, wie durch das blaue Rechteck hervorgehoben. Insbesondere beinhaltet die Hauptlogik die Funktion computeSwapStep und die Funktion _updateLiquidityAndCrossTick. Die erstere berechnet Schlüsselzustände wie Ein- und Ausgabemengen für den gegebenen Swap und nextSqrtP, während die letztere Fälle behandelt, wenn ein Tick überquert wird.

Traditionell, wenn der Preis steigt, sprechen wir von einer Rechts-/Aufwärtsverschiebung des Ticks; andernfalls sagen wir, der Tick bewegt sich nach Links/Unten.

Um die später zu diskutierende Schwachstelle besser zu verstehen, ist es unerlässlich, die relevante Code-Logik der Funktion computeSwapStep zu untersuchen, wie in der folgenden Abbildung dargestellt:

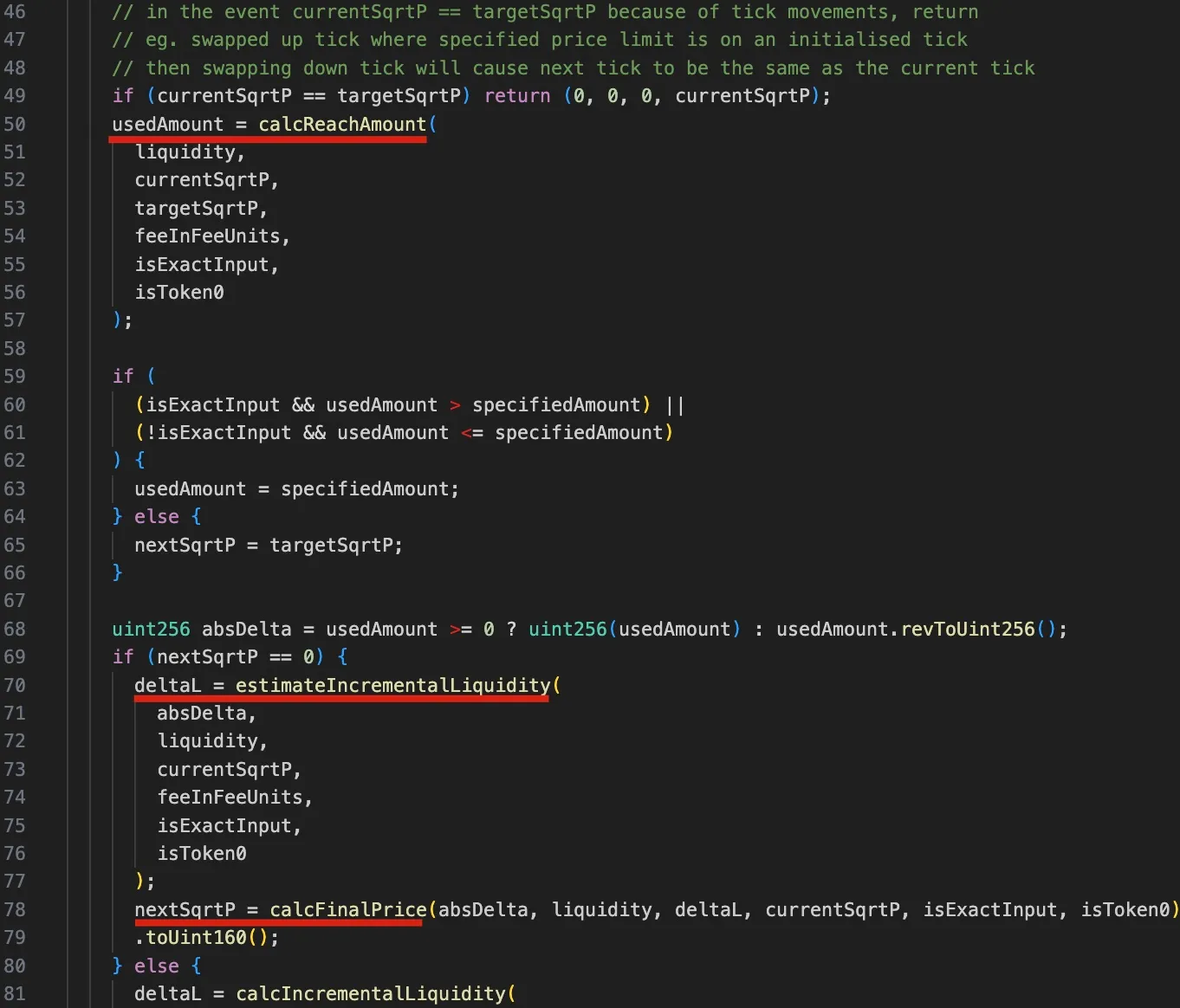
Zuerst wird von Zeile 50 bis 57 die Funktion calcReachAmount aufgerufen, um die benötigte Menge an Eingabetoken zu berechnen, um den targetSqrtP (nächster Tick oder benutzerdefinierter Zielpreis) zu erreichen.

Als nächstes wird zwischen Zeile 59 und 62 ein Test durchgeführt, um zu bestimmen, ob der Tick überquert werden soll oder nicht.

Insbesondere, wenn die verwendete Menge (usedAmount) größer ist als die vom Benutzer angegebene Menge (specifiedAmount) bei exaktem Eingabe-Swap (der im Angriff verwendete Fall), bedeutet dies, dass der Tick nicht überquert werden sollte und der nextSqrtP aus der inkrementellen Liquidität (deltaL, d.h. der Delta-Liquidität) abgeleitet werden muss.

Anschließend wird zwischen Zeile 70 und 79 der ΔL (deltaL) aus der Eingabemenge, der aktuellen Liquidität und dem Preis mit der Funktion estimateIncrementalLiquidity abgeleitet. Schließlich wird der Endpreis nach dem Swap nextSqrtP anhand von deltaL, Eingabemenge, aktuellem Preis und Liquidität mit der Funktion calcFinalPrice berechnet.

Umgekehrt, wenn die benötigte Menge kleiner ist als die vom Benutzer angegebene Menge (was bedeutet, dass nextSqrtP > 0), wird deltaL anhand des aktuellen und des Ziel-sqrtP berechnet, und nextSqrtP ist der sqrtP des nächsten Ticks. Die Details werden weggelassen, da dieser Zweig im Angriff nicht verwendet wird.

Die oben beschriebenen Schritte verdeutlichen, dass, wenn der Tick nicht überquert wird, der von computeSwapStep zurückgegebene nextSqrtP nicht größer sein sollte als der sqrtP des nächsten Ticks. Aufgrund der Abhängigkeit des Preises von der Liquidität (Basisliquidität und Delta-Liquidität) und des Präzisionsverlusts ist es dem Angreifer jedoch möglich, den nextSqrtP so zu manipulieren, dass er größer wird, während der Tick nicht überquert wird.

0x2 Schwachstellenanalyse

Die Grundursache liegt in der fehlerhaften Tick-Berechnung, die durch die falsche Rundungsrichtung innerhalb der Delta-Liquiditätsberechnung (d.h. der Funktion estimateIncrementalLiquidity) des SwapMath-Vertrags (der von der Funktion computeSwapStep aufgerufen wird) verursacht wird. Dies beeinträchtigt wiederum die spätere Tick-Berechnung.

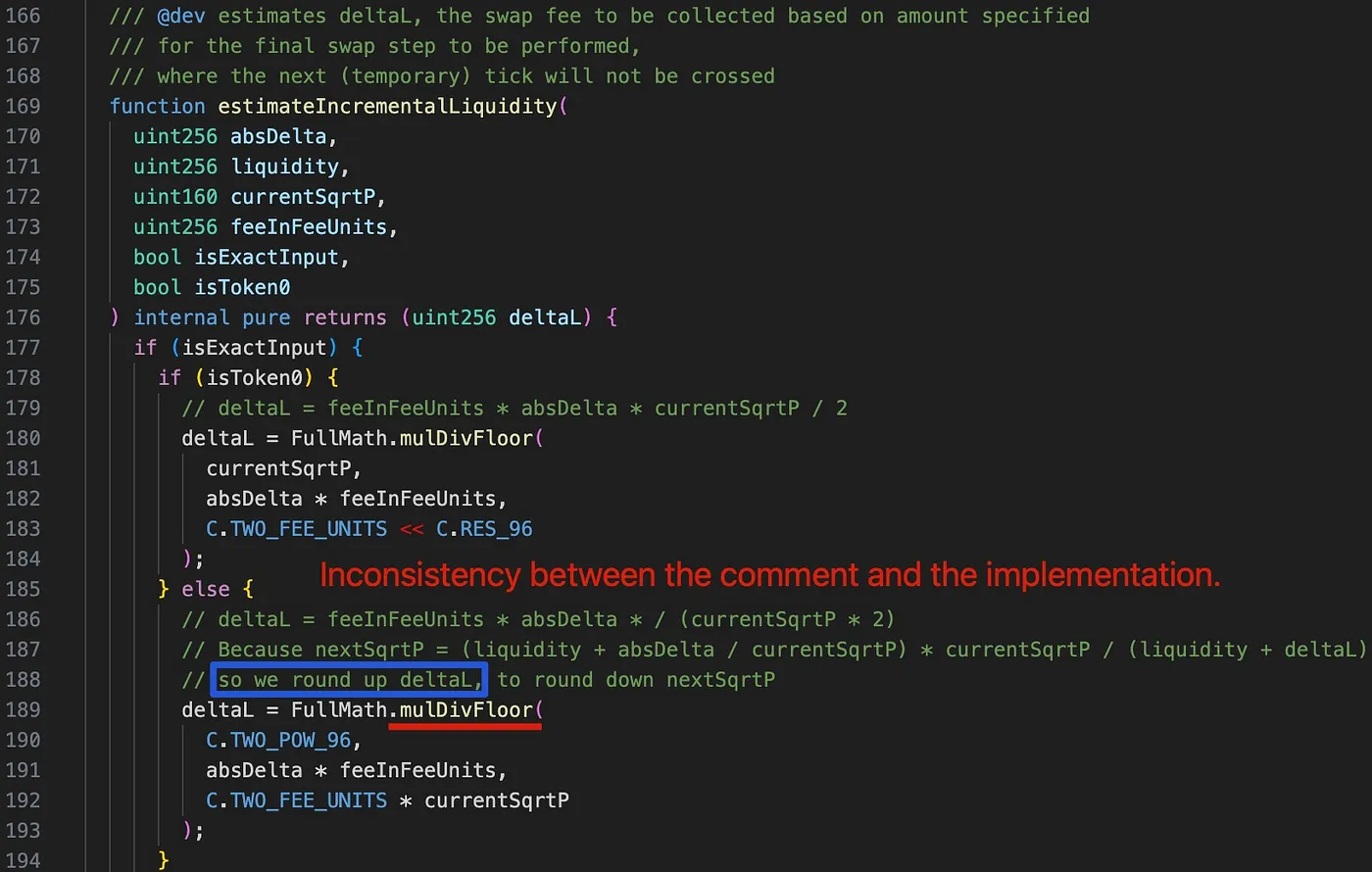
Interessanterweise stellen wir bei der Untersuchung des Kommentars in Zeile 188 (hervorgehoben durch das blaue Rechteck) fest, dass deltaL aufgerundet werden soll, um nextSqrtP abzurunden. deltaL wird jedoch versehentlich abgerundet, da die Funktion mulDivFloor in Zeile 189 verwendet wird. Folglich wird nextSqrtP fälschlicherweise aufgerundet.

0x3 Angriffsanalyse

Die Angreifer initiierten mehrere Angriffstransaktionen, wobei jede Transaktion mehrere Pools leerte. Der Einfachheit halber basiert die folgende Diskussion auf dem ersten Angriff innerhalb der Angriffstransaktion.

Die Kernangrifflogik besteht aus den folgenden sechs Schritten:

Ausleihen von 2.000 WETH über einen Flash-Loan von AAVE.
Tauschen von 6,850 WETH gegen 6,371 frxETH im geschädigten Pool 0xfd7b. Dieser Schritt dient dazu, den aktuellen Tick und currentSqrtP an eine Stelle zu verschieben, an der derzeit keine Liquidität vorhanden ist.

currentSqrtP scheint vom Angreifer zufällig gewählt zu werden, und der Swap stoppt genau bei diesem Preis.
Die Basisliquidität (baseL) ist nach diesem Schritt Null, aber die Reinvestitionsliquidität (reinvestL) ist ungleich Null.

Hinzufügen von Liquidität zum Pool und anschließendes Entfernen eines Teils der Liquidität. Dieser Schritt dient zur Kontrolle des Bereichs und der Gesamtliquidität auf einen gewünschten Betrag.

Der Tickbereich wird basierend auf dem currentSqrtP gewählt.
Die gewünschte Liquidität für den Angriff könnte aus dem Tickbereich abgeleitet werden, obwohl die entsprechende Berechnungslogik weiter untersucht werden muss.

Tauschen von 387,170 WETH gegen 0,06 frxETH im Pool. Dieser Schritt dient zur Manipulation des aktuellen Ticks, sodass nextTick == currentTick.

Der Eingabebetrag wird basierend auf der Liquidität und dem currentSqrtP gewählt.

Tauschen von 0,06 frxETH gegen 396,244 WETH im Pool. Beachten Sie, dass die Tauschrichtung gegenüber dem vorherigen Schritt entgegengesetzt ist. In diesem Schritt wird die Liquidität doppelt gezählt, um den Tausch profitabel zu machen und folglich den Pool zu leeren.
Zurückzahlen des Flash-Loans und Ernten von 6,364 WETH und 1,117 frxETH.

Offensichtlich sind die letzten beiden Swaps (Schritt 4 und Schritt 5) die entscheidenden Angriffsschritte zur Manipulation der Tick-Berechnung und zur profitablen Durchführung des Swaps zur Leerung des Pools. Wir werden die Details in den folgenden Unterabschnitten erläutern.

Es ist wichtig zu beachten, dass Schritt 3 für die Manipulation der Liquidität entscheidend ist. Aufgrund der Notwendigkeit einer präzisen Tick-Manipulation durch die Rundungsoperation ist es unmöglich, das Ziel durch direktes Hinzufügen von Liquidität zu erreichen. Die Entfernung von Liquidität dient dazu, die Liquidität im Bereich genau so zu steuern, wie es der Angreifer wünscht.

0x3.1 Schritt 4: Manipulation des aktuellen Ticks und `currentSqrtP`

Nach den vorherigen Schritten (Schritt 1 und 2) hat der Angreifer den Tickbereich und die Liquidität für die Manipulation vorbereitet. Insbesondere:

currentSqrtP befindet sich an einer gewünschten Stelle
Aktueller Tick = 110.909 und nächster Tick = 111.310, die den currentSqrtP umgeben

Dieser Schritt tauscht WETH gegen frxETH. In der Funktion computeSwapStep haben wir die folgende Ausführungsspur:

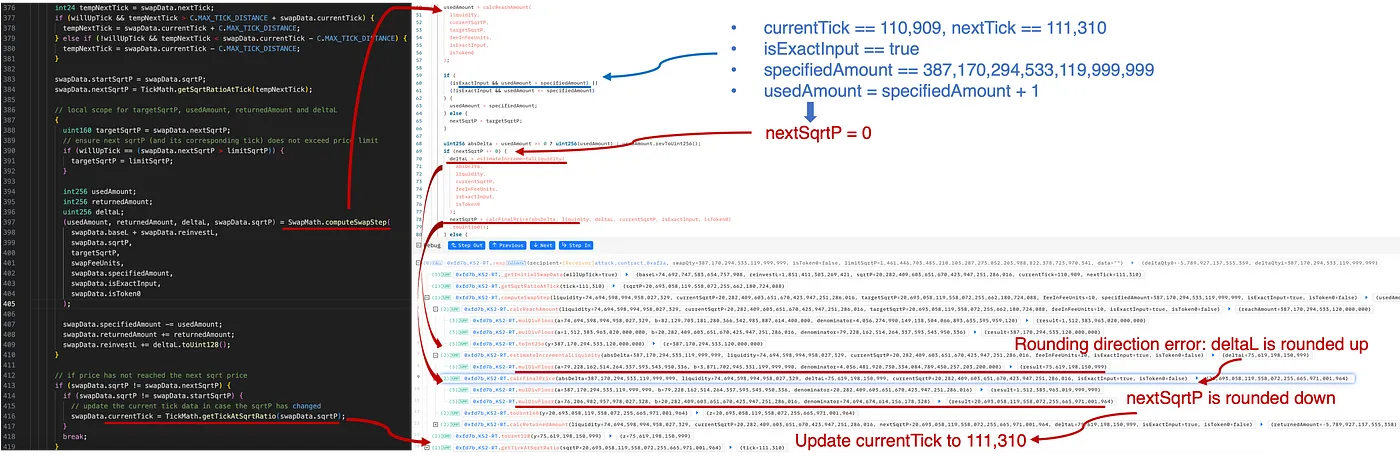
Wie in der obigen Abbildung gezeigt, wird die Menge zur Erreichung des Ziels (d.h. des nächsten Ticks) durch Aufruf der Funktion calcReachAmount berechnet:

usedAmount = calcReachAmount(liquidity, currentSqrtP, targetSqrtP)

Es ist zu beachten, dass diese Berechnung vor dem Swap abgeleitet werden kann. Durch sorgfältige Wahl von specifiedAmount (usedAmount = specifiedAmount + 1) steuerte der Angreifer den Swap so, dass das Ziel (d.h. der nächste Tick 111.310) nicht erreicht wurde, was dazu führte, dass nextSqrtP = 0 war.

In dieser Situation, da der Tick nicht überquert wird, muss nextSqrtP (d.h. der Endpreis) aus der Delta-Liquidität (angesammelt als Swap-Gebühren) abgeleitet werden.

Zuerst wird die inkrementelle Liquidität deltaL aus den Gebühren berechnet durch:

deltaL = estimateIncrementalLiquidity(absDelta, currentSqrtP)

Dann der Endpreis nextSqrtP:

nextSqrtP = calcFinalPrice(absDelta, liquidity, deltaL, currentSqrtP)

Wenn wir den Rundungsrichtungsfehler aus dem vorherigen Abschnitt nochmals betrachten, unterscheiden sich hier die Berechnungsergebnisse aufgrund unterschiedlicher Rundungsrichtungen aufgrund des fehlerhaften Rundens von deltaL:

Daher sind nach der Tick-Manipulation in Schritt 4 die aktuellen Zustände wie folgt zusammengefasst:

currentSqrtP ist 20.693.058.119.558.072.255.665.971.001.964, leicht größer als der sqrtP bei Tick 111.310 (sqrtP bei 111.310 = 20.693.058.119.558.072.255.662.180.724.088).
Aktueller Tick = 111.310 und nächster Tick = 111.310

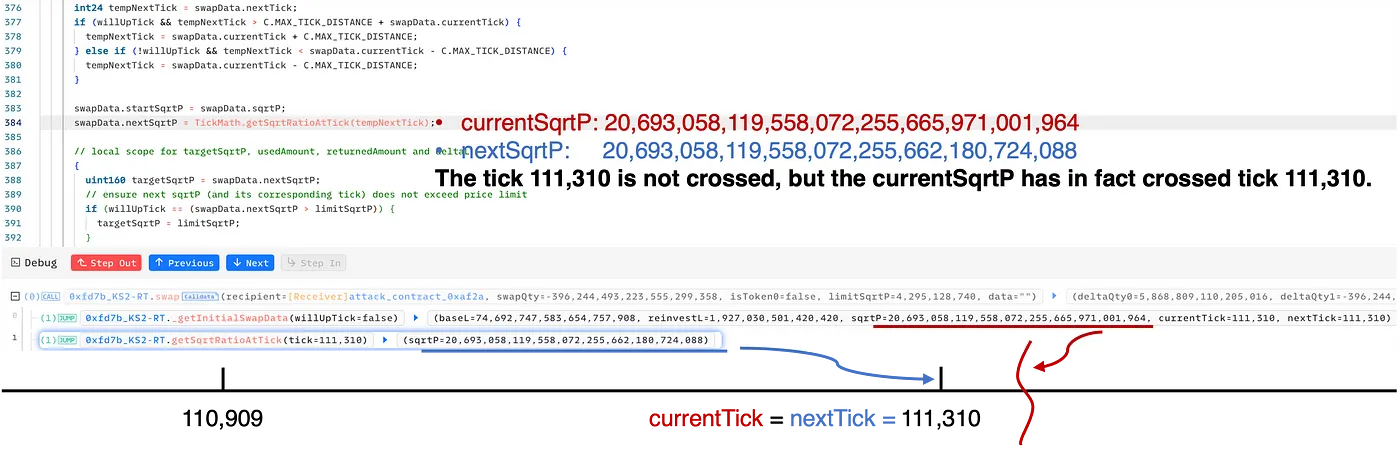
Wie in der obigen Abbildung dargestellt, täuscht der Swap in Schritt 4 den Pool geschickt, indem er vorgibt, dass der Tick 111.310 nicht überquert wird. In Wirklichkeit ist der currentSqrtP jedoch tatsächlich größer als der sqrtP des Ticks 111.310.

0x3.2 Schritt 5: doppelte Liquiditätszählung

Basierend auf der Manipulation in Schritt 4 ist die Angrifflogik in Schritt 5 reasonably straightforward. Zu diesem Zeitpunkt orchestrierte der Angreifer einen umgekehrten Swap von frxETH zu WETH, der den Tick und den currentSqrtP nach links verschieben würde. Insbesondere wird die Funktion computeSwapStep innerhalb der Schleife zweimal aufgerufen, was schließlich zur doppelten Liquiditätszählung[7] auf unvorhergesehene Weise führt und folglich zusätzliche Gewinne generiert.

Wie in der obigen Spur gezeigt:

Beim ersten Aufruf der Funktion computeSwapStep wurde der currentSqrtP auf den sqrtP von Tick 111.310 verschoben. Dies ist ein winziger Swap, der nur 3 Wei von frxETH verwendet, um tatsächlich Tick 111.310 zu erreichen. Anschließend, innerhalb der Funktion _updateLiquidityAndCrossTick, sollte der aktuelle Tick Tick 111.310 überqueren (nach links/unten), obwohl er in Schritt 4 nicht wirklich in Richtung rechts/oben Tick 111.310 durchquert hat. Dies führt dazu, dass die Liquidität bei Tick 111.310 doppelt gezählt wird.
Beim zweiten Aufruf der Funktion computeSwapStep kann die vorherige doppelte Zählung der Liquidität zu potenziellen zusätzlichen Gewinnen führen. Insbesondere durch Ausnutzung dieser doppelten Liquiditätszählung wird der Swap-Preis im abschließenden Schritt verzerrt, was zu einem größeren Betrag an ausgetauschtem WETH führt und somit einen Gewinn generiert.

0x4 Zusammenfassung von Angriffen und Gewinnen

Zum Zeitpunkt der Verfassung haben wir mehrere Angriffe auf verschiedenen Chains (einschließlich Ethereum, Optimism, Polygon, Arbitrum, Avalanche und Base) in freier Wildbahn beobachtet, die zu Verlusten von über 48 Mio. $ führten. Diese Angriffe wurden von verschiedenen Angreifern durchgeführt, wie folgt:

Eine vollständige Liste dieser Angriffstransaktionen wurde in einem von uns vorbereiteten Dokument gesammelt. Bitte beziehen Sie sich für detailliertere Informationen darauf.

0x5 Schlussfolgerung

Zusammenfassend lässt sich sagen, dass dies eine subtile Schwachstelle ist, die aus einer fehlerhaften Rundungslogik resultiert. Der Exploit ist unglaublich ausgeklügelt. Tatsächlich haben wir in diesem Jahr eine Reihe von Sicherheitsvorfällen im Zusammenhang mit Präzisionsverlustproblemen beobachtet, die erhebliche Herausforderungen für die Community darstellen.

Erneut zeigen diese kontinuierlichen Angriffe die Bedeutung proaktiver Gefahrenabwehr, einer Strategie, die potenzielle Verluste effektiv mindern kann.